BZOJ1001: [BeiJing2006]狼抓兔子【最短路+对偶图】
题目链接:https://www.lydsy.com/JudgeOnline/problem.php?id=1001
1001: [BeiJing2006]狼抓兔子
Time Limit: 15 Sec Memory Limit: 162 MB
Submit: 27684 Solved: 7127
Description
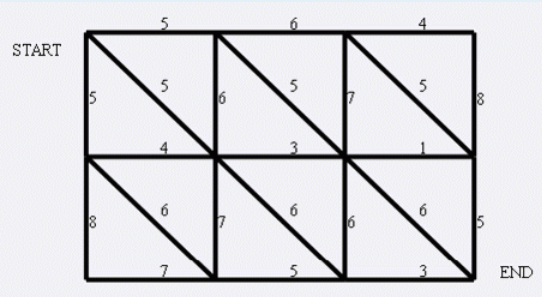
Input
Output
输出一个整数,表示参与伏击的狼的最小数量.
Sample Input
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
Sample Output
题外话:看着这图想到对偶图,然后就想起了bzoj2007海拔那题......
题解:题意就是求最小割,把平面图转化成对偶图然后从右上角到左下角跑dijkstra就可以了......注意双向边,数组开大点。
(一开始用vector写结果爆内存了,还是数组好用...)
#include<bits/stdc++.h>
#define CLR(a, b) memset((a), (b), sizeof((a)))
using namespace std;
const int INF = 1e9+;
const int N = 2e6+;
const int M = *N;
int head[N];
int d[N], vis[N];
struct Edge{
int v, c, nex;
}E[M];
int num = ;
void add(int u,int v,int c){
E[num].v = v; E[num].c = c; E[num].nex = head[u];
head[u] = num++;
}
struct qnode{
int v,c,x;
qnode(int _v=,int _c=,int _x=):v(_v),c(_c),x(_x){}
bool operator < (const qnode &r)const{
return r.c<c;
}
};
void dij(int s, int n) {//起点、终点
CLR(vis, );
for(int i = ; i <= n; i++) d[i] = INF;
priority_queue<qnode>q;
while(!q.empty()) q.pop();
d[s] = ;
q.push(qnode(s, ));
qnode t;
while(!q.empty()) {
t = q.top(); q.pop();
int u = t.v;
if(vis[u])continue;
vis[u] = true;
for(int i = head[u]; ~i; i = E[i].nex) {
int v = E[i].v;
int c = E[i].c;
if(!vis[v] && d[v] > d[u] + c) {
d[v] = d[u] + c;
q.push(qnode(v, d[v]));
}
}
}
}
int main() {
int n, m;
int k, i, j, u, v, w;
CLR(head,-); CLR(E, ); scanf("%d%d", &n, &m);
int s = ; //起点
int t = *(n-)*(m-)+;//终点 for(i = ; i <= n; ++i) {
for(j = ; j < m; ++j) {
scanf("%d", &w);
u = ( i==? s : (*(i-)-)*(m-)+j );
v = ( i==n? t : *(i-)*(m-)+j );
add(u, v, w); add(v, u, w);
}
}
for(i = ; i < n; ++i) {
for(j = ; j <= m; ++j) {
scanf("%d", &w);
u = ( j==m? s : *(i-)*(m-)+j-+m );
v = ( j==? t : *(i-)*(m-)+j- );
add(u, v, w); add(v, u, w);
}
}
for(i = ; i < n; ++i) {
for(j = ; j < m; ++j) {
scanf("%d", &w);
u = *(i-)*(m-)+j;
v = (*(i-)+)*(m-)+j;
add(u, v, w); add(v, u, w);
}
} dij(s, t);
printf("%d\n", d[t]);
return ;
}
2640ms
BZOJ1001: [BeiJing2006]狼抓兔子【最短路+对偶图】的更多相关文章
- BZOJ1001: [BeiJing2006]狼抓兔子 [最小割 | 对偶图+spfa]
1001: [BeiJing2006]狼抓兔子 Time Limit: 15 Sec Memory Limit: 162 MBSubmit: 19528 Solved: 4818[Submit][ ...
- [BZOJ1001] [Beijing2006] 狼抓兔子 (最短路)
Description 现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个 ...
- BZOJ1001 [BeiJing2006]狼抓兔子 最小割 对偶图 最短路
原文链接http://www.cnblogs.com/zhouzhendong/p/8686871.html 题目传送门 - BZOJ1001 题意 长成上面那样的网格图求最小割. $n,m\leq ...
- BZOJ1001 BeiJing2006 狼抓兔子 【网络流-最小割】*
BZOJ1001 BeiJing2006 狼抓兔子 Description 现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较 ...
- [BZOJ1001][BeiJing2006]狼抓兔子(最小割转最短路|平面图转对偶图)
1001: [BeiJing2006]狼抓兔子 Time Limit: 15 Sec Memory Limit: 162 MBSubmit: 31805 Solved: 8494[Submit][ ...
- BZOJ1001: [BeiJing2006]狼抓兔子(优化的dinic或转化对偶图求最短路)
1001: [BeiJing2006]狼抓兔子 Time Limit: 15 Sec Memory Limit: 162 MBSubmit: 30078 Solved: 7908[Submit][ ...
- BZOJ 1001: [BeiJing2006]狼抓兔子(最短路)
平面图的最小割转化为对偶图的最短路(资料:两极相通——浅析最大最小定理在信息学竞赛中的应用) ,然后DIJKSTRA就OK了. ------------------------------------ ...
- bzoj1001: [BeiJing2006]狼抓兔子 -- 最小割
1001: [BeiJing2006]狼抓兔子 Time Limit: 15 Sec Memory Limit: 162 MB Description 现在小朋友们最喜欢的"喜羊羊与灰太狼 ...
- bzoj1001: [BeiJing2006]狼抓兔子(初识是你最小割)
1001: [BeiJing2006]狼抓兔子 题目:传送门 题解: 听说这题当初是大难题...可惜当年没有网络流hahahha 现在用网络流的思想就很容易解决了嘛 给什么连什么,注意是双向边,然后跑 ...
随机推荐
- Bootstrap table 跨页全选
此代码是针对于bootstrap table中分页的跨页全选. 以下是整个bootstrap的定义 <script type="text/javascript" src=&q ...
- ios app真正的相互!!调用
1.需求:A应用打开B.B回跳到A 2.问题: 看到网络上的文档讲的大多数都是app单向跳转的例子,而我们在跳转到第二个app的时候往往需要返回到原来的app,虽然支付宝微信等第三方等应用会有回调 ...
- knockout事件绑定
<!DOCTYPE html> <html> <head> <meta charset="utf-8" /> <title&g ...
- hdu2036(多边形面积)
Description “ 改革春风吹满地, 不会AC没关系; 实在不行回老家, 还有一亩三分地. 谢谢!(乐队奏乐)” 话说部分学生心态极好,每天就知道游戏,这次考试如此简单的题目,也是云里雾里,而 ...
- 穿过代理获取真正的IP
/// <summary> /// 获取真ip /// </summary> /// <returns></returns> public string ...
- Spring Boot统一异常处理方案示例
一.异常处理的原则 1.调用方法的时候返回布尔值来代替返回null,这样可以 NullPointerException.由于空指针是java异常里最恶心的异常. 2. catch块里别不写代码.空ca ...
- c#设计模式·结构型模式
看的过程中,发现好多模式都用过,只是没有总结,或者是不知道叫这个名字吧··· 这里列举结构型模式,适配器.桥接.过滤.组合.装饰器.外观.享元.代理, 适配器模式:将现存的对象放到新的环境里边去,但是 ...
- python学习之老男孩python全栈第九期_day013知识点总结
# l = [1,2,3]# 索引# 循环 for # list # dic # str # set # tuple # f = open() # range() # enumerate'''prin ...
- 通过UA判断,对滚动条样式进行不同的操作
浏览器滚动条的默认样式比较丑,有些情况下,又不能直接overflow:hidden掉. 本文阐述如何通过 document.styleSheets[0].insertRule 简单的实现pc端和移动端 ...
- 【canvas系列】用canvas实现一个colorpicker(类似PS的颜色选择器)
每个浏览器都有自己的特点,比如今天要做的colorpicker就是,一千个浏览器,一千个哈姆雷特,一千个colorpicker.今天canvas系列就用canvas做一个colorpicker. ** ...
