poj3233 Matrix Power Series（矩阵快速幂）

题目要求的是 A+A²+...+A^k，而不是单个矩阵的幂。

　　那么可以构造一个分块的辅助矩阵 S，其中 A 为原矩阵，E 为单位矩阵，O 为0矩阵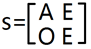   

　　将 S 取幂，会发现一个特性：

　　S^k +1右上角那一块不正是我们要求的 A+A²+...+A^k

　　于是构造出 S 矩阵，然后对它求矩阵快速幂即可，最后别忘了减去一个单位阵。

　　时间降为O(n³log₂k)

PS.减去单位矩阵的过程中要防止该位置小于零。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define maxn 65
 using namespace std;
 struct mat{
     long long a[maxn][maxn];
 };
 mat res,c;
 int n,k,m;
 mat mat_mul(mat &x,mat &y,int Mod){
     mat ans;
     memset(ans.a,,sizeof(ans.a));
     for (int i=;i<*n;i++)
         for (int j=;j<*n;j++)
         for (int kk=;kk<*n;kk++){
             ans.a[i][j]+=x.a[i][kk]*y.a[kk][j];
             ans.a[i][j]%=Mod;
         }
     return ans;
 }
 void mat_pow(mat &res,int k,int Mod){
     mat c=res;
     k--;
     while (k){
         if (k&) res=mat_mul(res,c,m);
         k>>=;
         c=mat_mul(c,c,m);
     }
 }
 int main(){
     cin >> n >> k >> m;
     memset(res.a,,sizeof(res.a));
     for (int i=;i<n;i++){
         for (int j=;j<n;j++){
             cin >> res.a[i][j];
         }
         res.a[i][i+n]=res.a[i+n][i+n]=;
     }
     mat_pow(res,k+,m);       //求出res的k+1次方
     for (int i=;i<n;i++){
         res.a[i][i+n]--;
         while (res.a[i][i+n]<) res.a[i][i+n]+=m;
     }
     for (int i=;i<n;i++){
         for (int j=;j<n-;j++){
             cout << res.a[i][j+n] << " ";
         }
         cout << res.a[i][*n-] << endl;
     }
     return ;
 }