A simple dispiction of dijkstra

前言

• \(SPFA\)算法由于它上限 \(O(NM) = O(VE)\)的时间复杂度,被卡掉的几率很大.在算法竞赛中,我们需要一个更稳定的算法:\(dijkstra\).

什么是\(dijkstra\)?

• \(dijkstra\)是一种单源最短路径算法,时间复杂度上限为\(O(n^2)\)(朴素),在实际应用中较为稳定\(;\)加上堆优化之后更是具有\(O((n+m)\log_{2}n)\)的时间复杂度,在稠密图中有不俗的表现.

\(dijkstra\)的原理/流程?

• \(dijkstra\)本质上的思想是贪心,它只适用于不含负权边的图.
• 我们把点分成两类,一类是已经确定最短路径的点,称为"白点",另一类是未确定最短路径的点,称为"蓝点"
• \(dijkstra\)的流程如下\(:\)
• \(1.\) 初始化\(dis[start] = 0,\)其余节点的\(dis\)值为无穷大.
• \(2.\) 找一个\(dis\)值最小的蓝点\(x,\)把节点\(x\)变成白点.
• \(3.\) 遍历\(x\)的所有出边\((x,y,z),\)若\(dis[y] > dis[x] + z,\)则令\(dis[y] = dis[x] + z\)
• \(4.\) 重复\(2,3\)两步,直到所有点都成为白点\(.\)
• 时间复杂度为\(O(n^2)\)

\(dijkstra\)为什么是正确的

• 当所有边长都是非负数的时候,全局最小值不可能再被其他节点更新.所以在第\(2\)步中找出的蓝点\(x\)必然满足\(:dis[x]\)已经是起点到\(x\)的最短路径\(.\)我们不断选择全局最小值进行标记和拓展,最终可以得到起点到每个节点的最短路径的长度

图解

• (令\(start = 1\))
• 开始时我们把\(dis[start]\)初始化为\(0\),其余点初始化为\(inf\)
  
  
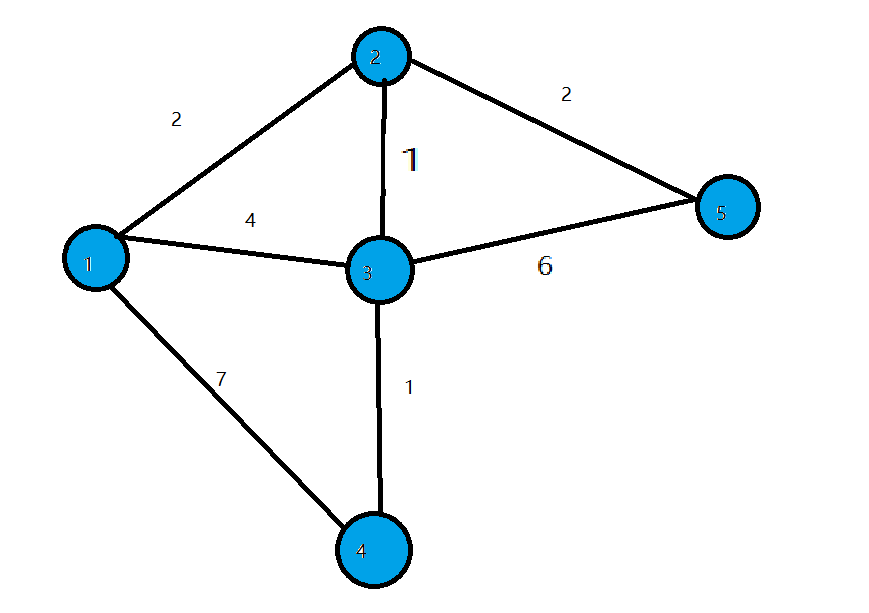
• 第一轮循环找到\(dis\)值最小的点\(1\),将\(1\)变成白点,对所有与\(1\)相连的蓝点的\(dis\)值进行修改,使得\(dis[2]=2,dis[3]=4,dis[4]=7\)
  
  
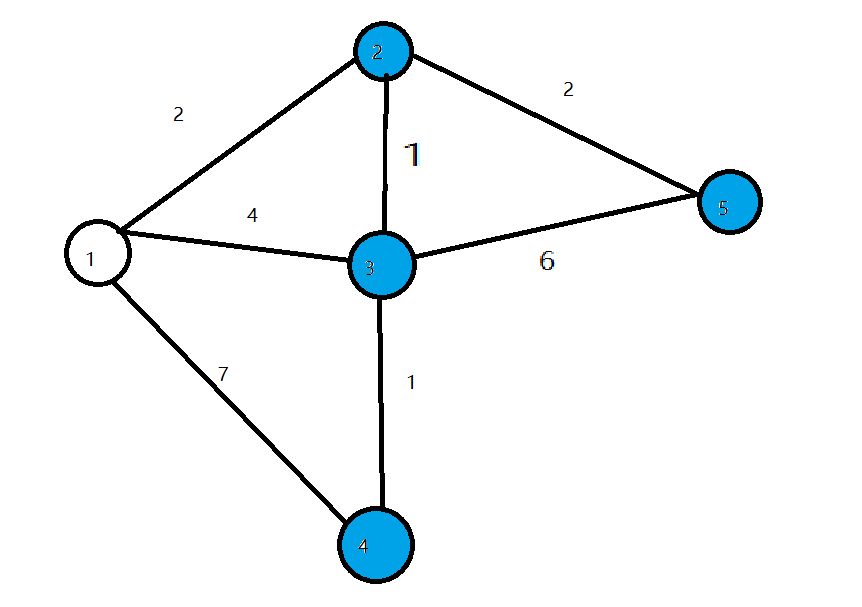
• 第二轮循环找到\(dis\)值最小的点\(2\),将\(2\)变成白点,对所有与\(2\)相连的蓝点的\(dis\)值进行修改,使得\(dis[3]=3,dis[5]=4\)
  
  
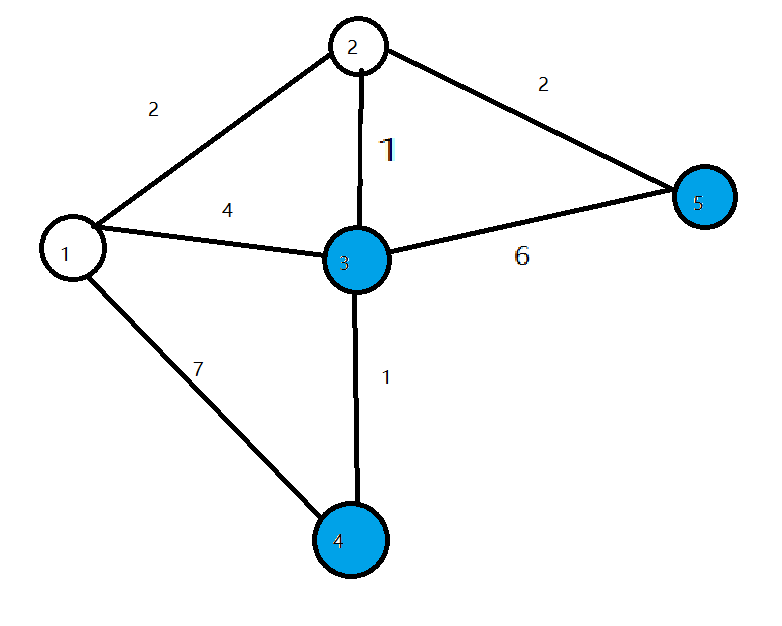
• 第三轮循环找到\(dis\)值最小的点\(3\),将\(3\)变成白点,对所有与\(2\)相连的蓝点的\(dis\)值进行修改,使得\(dis[4]=4\)
  
  
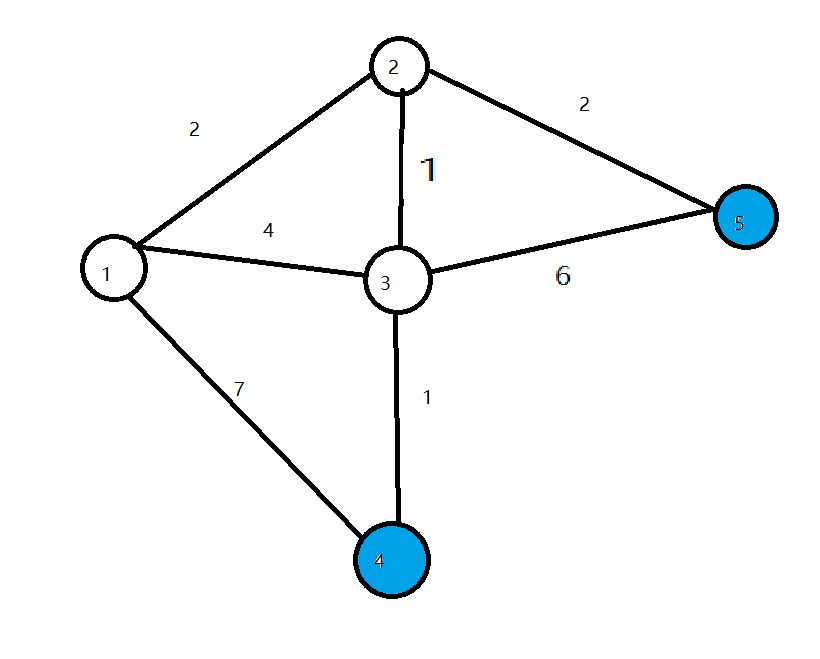
• 接下来两轮循环分别将\(4,5\)设为白点,算法结束,求出所有点的最短路径
• 时间复杂度\(O(n^2)\)

为什么\(dijkstra\)不能处理有负权边的情况?

• 我们来看下面这张图
  
  
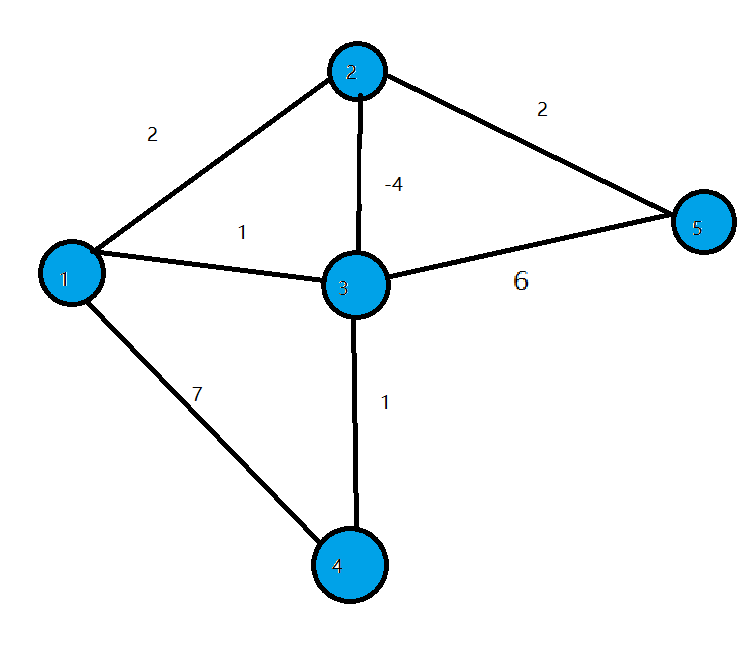
• \(2\)到\(3\)的边权为\(-4\),显然从\(1\)到\(3\)的最短路径为\(-2\) \((1->2->3).\)但在循环开始时程序会找到当前\(dis\)值最小的点\(3\),并标记它为白点.
• 这时的\(dis[3]=1,\)然而\(1\)并不是起点到\(3\)的最短路径.因为\(3\)已经被标为白点,所以\(dis[3]\)不会再被修改了.我们在边权存在负数的情况下得到了错误的答案.

\(dijkstra\)的堆优化?

• 观察\(dijkstra\)的流程,发现步骤\(2\)可以优化

• 怎么优化呢?

• 我会zkw线段树!我会斐波那契堆!

• 我会堆!

• 我们可以用堆对\(dis\)数组进行维护,用\(O(\log_{2}n)\)的时间取出堆顶元素并删除,用\(O(\log_{2}n)\)遍历每条边,总复杂度\(O((n+m)\log_{2}n)\)

• 范例代码:

#include<bits/stdc++.h>

const int MaxN = 100010, MaxM = 500010;

struct edge
{
    int to, dis, next;
};

edge e[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;

inline void add_edge( int u, int v, int d )
{
    cnt++;
    e[cnt].dis = d;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

struct node
{
    int dis;
    int pos;
    bool operator <( const node &x )const
    {
        return x.dis < dis;
    }
};

std::priority_queue<node> q;

inline void dijkstra()
{
    dis[s] = 0;
    q.push( ( node ){0, s} );
    while( !q.empty() )
    {
        node tmp = q.top();
        q.pop();
        int x = tmp.pos, d = tmp.dis;
        if( vis[x] )
            continue;
        vis[x] = 1;
        for( int i = head[x]; i; i = e[i].next )
        {
            int y = e[i].to;
            if( dis[y] > dis[x] + e[i].dis )
            {
                dis[y] = dis[x] + e[i].dis;
                if( !vis[y] )
                {
                    q.push( ( node ){dis[y], y} );
                }
            }
        }
    }
}

int main()
{
    scanf( "%d%d%d", &n, &m, &s );
    for(int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
    for( register int i = 0; i < m; ++i )
    {
        register int u, v, d;
        scanf( "%d%d%d", &u, &v, &d );
        add_edge( u, v, d );
    }
    dijkstra();
    for( int i = 1; i <= n; i++ )
        printf( "%d ", dis[i] );
    return 0;
}

例题

• 入门模板:P3371
• 进阶模板:P4779
• 其余例题请右转洛谷题库,搜索"最短路"

后记

• 本文部分内容摘自李煜东《算法竞赛进阶指南》和《信息学竞赛一本通》
• 友情提示:正权图请使用\(dijkstra\)算法,负权图请使用\(SPFA\)算法