JDOJ 3055: Nearest Common Ancestors

JDOJ 3055: Nearest Common Ancestors

JDOJ传送门

Description

给定N个节点的一棵树，有K次查询，每次查询a和b的最近公共祖先。

样例中的16和7的公共祖先(LCA:Least Common Ancestors)是4。

Input

第一行两个整数N(1 < N <= 105)、K(1 <= K <= 105)

第2~N行，每行两个整数a、b(1 <= a,b <= N)，表示a是b的父亲。

第N+1~N+K+1行，每行两个整数a、b(1 <= a,b <= N)，表示询问a和b的最近公共祖先是谁。

Output

输出K行，第i行表示第i个查询的最近公共祖先是谁。

Sample Input

16 1 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7

Sample Output

4

HINT

30%数据 N<=20，K<=5。小数据，方便调试

50%数据 N<=1000，K<=1000。中数据，暴力可过

100%数据 1 < N <= 105，1 <= K <= 105。大数据，请使用树上倍增、LCA转RMQ&ST、离线Tarjan、树链剖分求LCA

Source

POJ1330改

本题历史背景：

本题初次使用C++语言提交于2019.9.11晚20:01

看到没有人用C语言交，就用原代码混了C语言榜首第一。

但是却被\(iamrjj\)给顶了。为了防止我夺回第一，他用了各种技巧把时间提到了64ms，却死活不告诉我算法和代码实现方式。

当然，顺带着，他还Diss了我几句。

UPD:2019.9.12 晚19:21

正义终归是正义@ysy20021208

在机房大佬的帮助加各种卡常技巧加我++的RP（行正则正）

我终于夺回了被\(iamrjj\)临时掌控的榜首位置

时间是这样的（为了防止\(iamrjj\)盗代码我不贴代码和改进思路，有对此好奇的请私聊我）

256ms--104ms--60ms--48ms

上两发最优解证明：

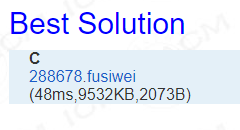
在此建议大家：

不要怕这类事情发生，有些位置天生就属于一个人，只要肯付出努力，谁也抢不走。

题解：

这道题就是LCA的裸题

只不过我这次用了倍增，又心血来潮卡了C语言的最优解。

所以附上代码，如果倍增LCA不太会的同学请参考我的博客补习：

博客链接：

求LCA问题

#include<stdio.h>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
int n,k,tot,root;
int fa[200008];
int head[200008],nxt[200008],to[200008];
int deep[200008],v[200008],f[200008][21];
int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'|| ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
        x=x*10+ch-'0',ch=getchar();
    return x*f;
}
void add(int x,int y)
{
    to[++tot]=y;
    nxt[tot]=head[x];
    head[x]=tot;
}
void dfs(int x)
{
    v[x]=1;
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(v[y]==1)
            continue;
        deep[y]=deep[x]+1;
        f[y][0]=x;
        dfs(y);
    }
}
int lca(int x,int y)
{
    if(deep[x]<deep[y])
    {
        int t=y;
        y=x;
        x=t;
    }
    for(int i=20;i>=0;i--)
        if(deep[f[x][i]]>=deep[y])
            x=f[x][i];
    if(x==y)
        return x;
    for(int i=20;i>=0;i--)
        if(f[x][i]!=f[y][i])
        {
            x=f[x][i];
            y=f[y][i];
        }
    return f[x][0];
}
int main()
{
    n=read();k=read();
    for(int i=1;i<n;i++)
    {
        int x,y;
        x=read();y=read();
        add(x,y);
        add(y,x);
        fa[y]=x;
    }
    for(int i=1;i<=n;i++)
        if(fa[i]==0)
        {
            root=i;
            break;
        }
    deep[root]=1;
    dfs(root);
    for(int i=1;i<=20;i++)
        for(int j=1;j<=n;j++)
            f[j][i]=f[f[j][i-1]][i-1];
    for(int i=1;i<=k;i++)
    {
        int x,y;
        x=read();y=read();
        printf("%d\n",lca(x,y));
    }
    return 0;
}