Codeforces Round #576 (div.1 + div.2)

Div2

A

长度为\(n(n≤10^5)\)的数组，每个元素不同，求有多少个位置\(d\)满足\(d - x \le j < d \And d < j \le d + y a_d<a_j(0\le x,y\le 7)\)

\(x,y\)较小，遍历每个位置，暴力判断即可

B

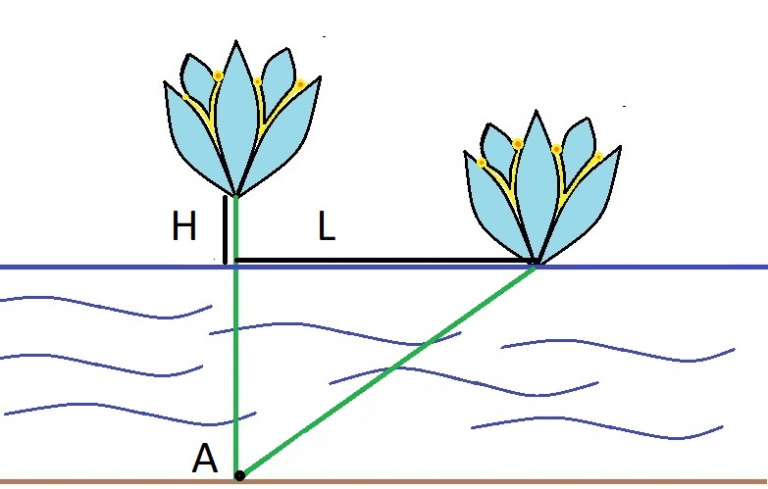
如下图，给出\(L,H\)，求水面深度

设水面深度为\(x\)，勾股定理：\(x^2+L^2=(x+H)^2\)，解得\(x=\frac{L^2-H^2}{2H}\)

Div1

A

长度为\(n(1 \le n \le 4 \cdot 10^{5})\)的数组和\(I(1 \le I \le 10^{8})\)，确定一个范围\([L,R]\)，使得该范围内数组的元素个数\(K\)(\(满足\)\lceil log_{2} K \rceil\cdot n≤8I)$。求不在此范围内的元素最少为多少

得出最大\(K\)，将原数组排序去重离散得到一个排列及每个数字出现的次数
转换为：\(1\~ tot\)的数字，给出每个数字出现的次数，选连续\(K\)个数字，求未选中数字的最小个数

判断选择\([1,K],[2,K+1],[n-K+1,n]\)，没被选中的数字至多为首尾连续两段，预处理前缀和和后缀和暴力判断即可

B

长度为\(n\)的数组，和\(q\)次操作
两种操作\(1.a_x=p\)，\(2.\)数组里小于\(x\)的全部修改为\(x\)

有没有写平衡树的呀
单独考虑\(a_x\)，第一种操作的影响为最后一次修改\(x\)位置的值\(p\)，第二种操作的影响为最后一次操作一后的每次操作

统计每个\(x\)最后一次操作一的位置，并对第二种操作统计最大后缀，最后取\(max\)

C

\(3\cdot n\)个点\(m\)条边，选出\(n\)大小的独立点集或独立边集\(1 \leq n \leq 10^{5},0 \leq m \leq 5 \cdot 10^{5}\)

随便选边，设独立边集为\(len\)

• \(len≥n\)：输出边集

• \(len<n\)：输出没在边集里的大小为\(n\)的点集\((\)点集的最大大小为\(3\cdot n-2(n-1)≥n)\)

D

\(n×n(1 \leq n \leq 50)\)的黑白色格子，将一块长\(h\)宽\(w\)的范围涂白，花费\(max(h,w)\)，求全涂白的最小花费

普及组的暴力？\(f_{x,y,xx,yy}\)为将\((x,y)(xx,yy)\)范围全涂白的最小花费，记忆化搜索即可

E

F