C#求任意两整数之和

2019.9.11

作业要求：

求出任意两整数之和

解决方案：

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;
 
 namespace ClassDemoExercise
 {
     class Program
     {
         static void Main(string[] args)
         {
             int i = Convert.ToInt32(Console.ReadLine());
             int j = Convert.ToInt32(Console.ReadLine());
             int num1 = Add(i,j);
             Console.WriteLine("数字相加之和是：{0}",num1);
             Console.Read();
         }
         static int Add(params int[] nums)
         {
             int sum = ;
             for(int i = ;i < nums.Length; i++)
             {
                 sum = sum + nums[i];
             }
             return sum;
         }
     }
 }

运行结果：

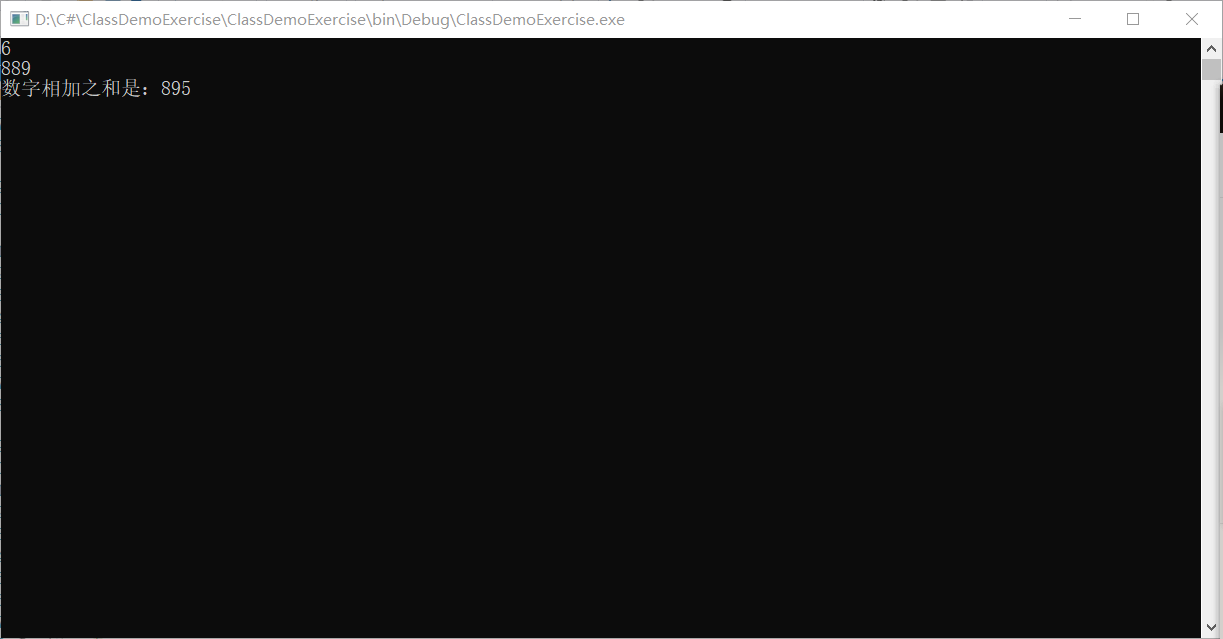
解题思路：

第一步，定义i，j两个变量

第二步，把i，j两个变量赋值给方法Add中

第三步，利用for循环，i判断与nums的长度大小，并利用此判断进行加和运算

第四步，返回值赋给num1，并输出num1

出现问题：

当代码第19行为

static int Add(params int nums[])

出现报错

解决方法：

将其改为

static int Add(params int[] nums)