跳表和ConcurrentSkipListMap解析

二分查找和AVL树查找

二分查找要求元素可以随机访问，所以决定了需要把元素存储在连续内存。这样查找确实很快，但是插入和删除元素的时候，为了保证元素的有序性，就需要大量的移动元素了。
如果需要的是一个能够进行二分查找，又能快速添加和删除元素的数据结构，首先就是二叉查找树，二叉查找树在最坏情况下可能变成一个链表。
于是，就出现了平衡二叉树，根据平衡算法的不同有AVL树，B-Tree，B+Tree，红黑树等，但是AVL树实现起来比较复杂，平衡操作较难理解，这时候就可以用SkipList跳跃表结构。

什么是跳表

传统意义的单链表是一个线性结构，向有序的链表中插入一个节点需要O(n)的时间，查找操作需要O(n)的时间。

跳跃表的简单示例：

如果我们使用上图所示的跳跃表，就可以减少查找所需时间为O(n/2)，因为我们可以先通过每个节点的最上面的指针先进行查找，这样子就能跳过一半的节点。

比如我们想查找19，首先和6比较，大于6之后，在和9进行比较，然后在和12进行比较......最后比较到21的时候，发现21大于19，说明查找的点在17和21之间，从这个过程中，我们可以看出，查找的时候跳过了3、7、12等点，因此查找的复杂度为O(n/2)。

查找的过程如下图：

其实，上面基本上就是跳跃表的思想，每一个结点不单单只包含指向下一个结点的指针，可能包含很多个指向后续结点的指针，这样就可以跳过一些不必要的结点，从而加快查找、删除等操作。对于一个链表内每一个结点包含多少个指向后续元素的指针，后续节点个数是通过一个随机函数生成器得到，这样子就构成了一个跳跃表。

随机生成的跳跃表可能如下图所示：

跳跃表其实也是一种通过“空间来换取时间”的一个算法，通过在每个节点中增加了向前的指针，从而提升查找的效率。

“Skip lists are data structures  that use probabilistic  balancing rather  than  strictly  enforced balancing. As a result, the algorithms  for insertion  and deletion in skip lists  are much simpler and significantly  faster
 than  equivalent  algorithms  for balanced trees.  ”
译文：跳跃表使用概率均衡技术而不是使用强制性均衡技术，因此，对于插入和删除结点比传统上的平衡树算法更为简洁高效。

跳表是一种随机化的数据结构，目前开源软件 Redis 和 LevelDB 都有用到它。

SkipList的操作

查找

查找就是给定一个key，查找这个key是否出现在跳跃表中，如果出现，则返回其值，如果不存在，则返回不存在。我们结合一个图就是讲解查找操作，如下图所示：

如果我们想查找19是否存在？如何查找呢？我们从头结点开始，首先和9进行判断，此时大于9，然后和21进行判断，小于21，此时这个值肯定在9结点和21结点之间，此时，我们和17进行判断，大于17，然后和21进行判断，小于21，此时肯定在17结点和21结点之间，此时和19进行判断，找到了。具体的示意图如图所示：

插入

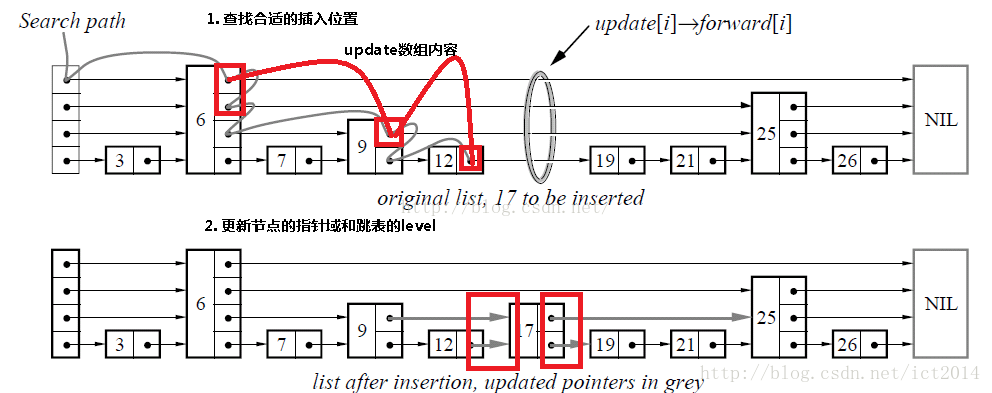
插入包含如下几个操作：1、查找到需要插入的位置   2、申请新的结点    3、调整指针。

我们结合下图进行讲解，查找路径如下图的灰色的线所示  申请新的结点如17结点所示， 调整指向新结点17的指针以及17结点指向后续结点的指针。这里有一个小技巧，就是使用update数组保存大于17结点的位置，update数组的内容如红线所示，这些位置才是有可能更新指针的位置。

删除

删除操作类似于插入操作，包含如下3步：1、查找到需要删除的结点 2、删除结点  3、调整指针

Key-Value数据结构

目前常用的key-value数据结构有三种：Hash表、红黑树、SkipList，它们各自有着不同的优缺点（不考虑删除操作）：
Hash表：插入、查找最快，为O(1)；如使用链表实现则可实现无锁；数据有序化需要显式的排序操作。
红黑树：插入、查找为O(logn)，但常数项较小；无锁实现的复杂性很高，一般需要加锁；数据天然有序。
SkipList：插入、查找为O(logn)，但常数项比红黑树要大；底层结构为链表，可无锁实现；数据天然有序。

如果要实现一个key-value结构，需求的功能有插入、查找、迭代、修改，那么首先Hash表就不是很适合了，因为迭代的时间复杂度比较高；而红黑树的插入很可能会涉及多个结点的旋转、变色操作，因此需要在外层加锁，这无形中降低了它可能的并发度。而SkipList底层是用链表实现的，可以实现为lock free，同时它还有着不错的性能（单线程下只比红黑树略慢），非常适合用来实现我们需求的那种key-value结构。
LevelDB、Reddis的底层存储结构就是用的SkipList。

基于锁的并发

优点：
1、编程模型简单，如果小心控制上锁顺序，一般来说不会有死锁的问题；
2、可以通过调节锁的粒度来调节性能。
缺点：
1、所有基于锁的算法都有死锁的可能；
2、上锁和解锁时进程要从用户态切换到内核态，并可能伴随有线程的调度、上下文切换等，开销比较重；
3、对共享数据的读与写之间会有互斥。

无锁编程（lock free）

常见的lock free编程一般是基于CAS(Compare And Swap)操作：CAS(void *ptr, Any oldValue, Any newValue);
即查看内存地址ptr处的值，如果为oldValue则将其改为newValue，并返回true，否则返回false。X86平台上的CAS操作一般是通过CPU的CMPXCHG指令来完成的。CPU在执行此指令时会首先锁住CPU总线，禁止其它核心对内存的访问，然后再查看或修改*ptr的值。简单的说CAS利用了CPU的硬件锁来实现对共享资源的串行使用。
优点：
1、开销较小：不需要进入内核，不需要切换线程；
2、没有死锁：总线锁最长持续为一次read+write的时间；
3、只有写操作需要使用CAS，读操作与串行代码完全相同，可实现读写不互斥。
缺点：
1、编程非常复杂，两行代码之间可能发生任何事，很多常识性的假设都不成立。
2、CAS模型覆盖的情况非常少，无法用CAS实现原子的复数操作。

而在性能层面上，CAS与mutex/readwrite lock各有千秋，简述如下：
1、单线程下CAS的开销大约为10次加法操作，mutex的上锁+解锁大约为20次加法操作，而readwrite lock的开销则更大一些。
2、CAS的性能为固定值，而mutex则可以通过改变临界区的大小来调节性能；
3、如果临界区中真正的修改操作只占一小部分，那么用CAS可以获得更大的并发度。
4、多核CPU中线程调度成本较高，此时更适合用CAS。
跳表和红黑树的性能相当，最主要的优势就是当调整(插入或删除)时，红黑树需要使用旋转来维护平衡性，这个操作需要动多个节点，在并发时候很难控制。而跳表插入或删除时只需定位后插入，插入时只需添加插入的那个节点及其多个层的复制，以及定位和插入的原子性维护。所以它更加可以利用CAS操作来进行无锁编程。

ConcurrentHashMap

JDK为我们提供了很多Map接口的实现，使得我们可以方便地处理Key-Value的数据结构。

当我们希望快速存取<Key, Value>键值对时我们可以使用HashMap。
当我们希望在多线程并发存取<Key, Value>键值对时，我们会选择ConcurrentHashMap。
TreeMap则会帮助我们保证数据是按照Key的自然顺序或者compareTo方法指定的排序规则进行排序。
OK，那么当我们需要多线程并发存取<Key, Value>数据并且希望保证数据有序时，我们需要怎么做呢？
也许，我们可以选择ConcurrentTreeMap。不好意思，JDK没有提供这么好的数据结构给我们。
当然，我们可以自己添加lock来实现ConcurrentTreeMap，但是随着并发量的提升，lock带来的性能开销也随之增大。
Don't cry......，JDK6里面引入的ConcurrentSkipListMap也许可以满足我们的需求。

什么是ConcurrentSkipListMap

ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList（跳表）结构实现，在理论上能够O(log(n))时间内完成查找、插入、删除操作。

存储结构

ConcurrentSkipListMap存储结构跳跃表（SkipList）：

1、最底层的数据节点按照关键字升序排列。

2、包含多级索引，每个级别的索引节点按照其关联数据节点的关键字升序排列。

3、高级别索引是其低级别索引的子集。

4、如果关键字key在级别level=i的索引中出现，则级别level<=i的所有索引中都包含key。

注：类比一下数据库的索引、B+树。

1.  
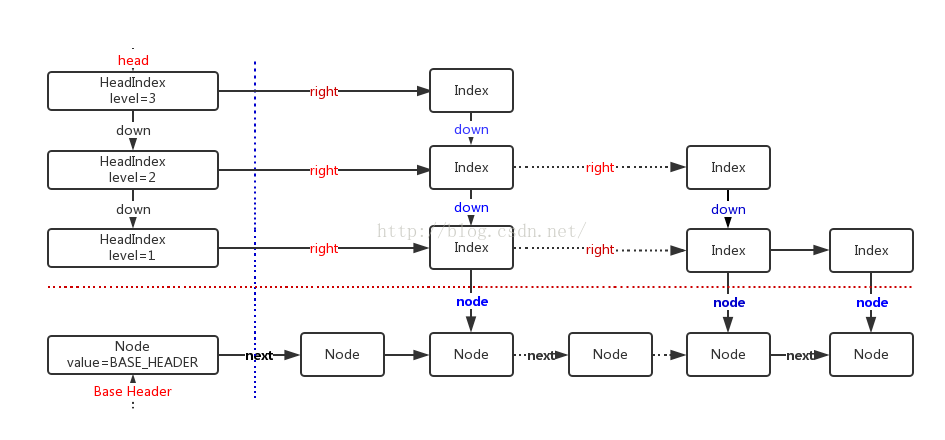
   public class ConcurrentSkipListMap<K,V> extends AbstractMap<K,V> implements ConcurrentNavigableMap<K,V>,
2.  
   Cloneable,java.io.Serializable {
3.  
     /** Special value used to identify base-level header*/
4.  
     private static final Object BASE_HEADER = new Object();//该值用于标记数据节点的头结点
5.  
    
6.  
   /** The topmost head index of the skiplist.*/
7.  
   private transient volatile HeadIndex<K,V> head;//最高级别索引的索引头
8.  
   ......
9.  
   /** Nodes hold keys and values, and are singly linked in sorted order, possibly with some intervening marker nodes.
10.  
    The list is headed by a dummy node accessible as head.node. The value field is declared only as Object because it
11.  
    takes special non-V values for marker and header nodes. */
12.  
    static final class Node<K,V> {//保存键值对的数据节点，并且是有序的单链表。
13.  
    final K key;
14.  
    volatile Object value;
15.  
    volatile Node<K,V> next;//后继数据节点
16.  
    ......
17.  
    }
18.  
     
19.  
    /** Index nodes represent the levels of the skip list.
20.  
    Note that even though both Nodes and Indexes have forward-pointing fields, they have different types and are handled
21.  
    in different ways, that can't nicely be captured by placing field in a shared abstract class.
22.  
    */
23.  
    static class Index<K,V> {//索引节点
24.  
    final Node<K,V> node;//索引节点关联的数据节点
25.  
    final Index<K,V> down;//下一级别索引节点（关联的数据节点相同）
26.  
    volatile Index<K,V> right;//当前索引级别中，后继索引节点
27.  
    ......
28.  
    }
29.  
    /** Nodes heading each level keep track of their level.*/
30.  
    static final class HeadIndex<K,V> extends Index<K,V> {//索引头
31.  
    final int level;//索引级别
32.  
    HeadIndex(Node<K,V> node, Index<K,V> down, Index<K,V> right, int level) {
33.  
    super(node, down, right);
34.  
    this.level = level;
35.  
    }
36.  
    }
37.  
    ......
38.  
    }

查找

1.  
   //Returns the value to which the specified key is mapped, or null if this map contains no mapping for the key.
2.  
   public V get(Object key) {
3.  
   return doGet(key);
4.  
   }

1.  
   private V doGet(Object okey) {
2.  
   Comparable<? super K> key = comparable(okey);
3.  
   // Loop needed here and elsewhere in case value field goes null just as it is about to be returned, in which case we
4.  
   // lost a race with a deletion, so must retry.
5.  
   // 这里采用循环的方式来查找数据节点，是为了防止返回刚好被删除的数据节点，一旦出现这样的情况，需要重试。
6.  
   for (;;) {
7.  
   Node<K,V> n = findNode(key);//根据key查找数据节点
8.  
   if (n == null)
9.  
   return null;
10.  
    Object v = n.value;
11.  
    if (v != null)
12.  
    return (V)v;
13.  
    }
14.  
    }

1.  
   /**Returns node holding key or null if no such, clearing out any deleted nodes seen along the way.
2.  
   Repeatedly traverses at base-level looking for key starting at predecessor returned from findPredecessor,
3.  
   processing base-level deletions as encountered. Some callers rely on this side-effect of clearing deleted nodes.
4.  
    
5.  
   * Restarts occur, at traversal step centered on node n, if:
6.  
   *
7.  
   * (1) After reading n's next field, n is no longer assumed predecessor b's current successor, which means that
8.  
   * we don't have a consistent 3-node snapshot and so cannot unlink any subsequent deleted nodes encountered.
9.  
   *
10.  
    * (2) n's value field is null, indicating n is deleted, in which case we help out an ongoing structural deletion
11.  
    * before retrying. Even though there are cases where such unlinking doesn't require restart, they aren't sorted out
12.  
    * here because doing so would not usually outweigh cost of restarting.
13.  
    *
14.  
    * (3) n is a marker or n's predecessor's value field is null, indicating (among other possibilities) that
15.  
    * findPredecessor returned a deleted node. We can't unlink the node because we don't know its predecessor, so rely
16.  
    * on another call to findPredecessor to notice and return some earlier predecessor, which it will do. This check is
17.  
    * only strictly needed at beginning of loop, (and the b.value check isn't strictly needed at all) but is done
18.  
    * each iteration to help avoid contention with other threads by callers that will fail to be able to change
19.  
    * links, and so will retry anyway.
20.  
    *
21.  
    * The traversal loops in doPut, doRemove, and findNear all include the same three kinds of checks. And specialized
22.  
    * versions appear in findFirst, and findLast and their variants. They can't easily share code because each uses the
23.  
    * reads of fields held in locals occurring in the orders they were performed.
24.  
    *
25.  
    * @param key the key
26.  
    * @return node holding key, or null if no such
27.  
    */
28.  
    private Node<K,V> findNode(Comparable<? super K> key) {
29.  
    for (;;) {
30.  
    Node<K,V> b = findPredecessor(key);//根据key查找前驱数据节点
31.  
    Node<K,V> n = b.next;
32.  
    for (;;) {
33.  
    if (n == null)
34.  
    return null;
35.  
    Node<K,V> f = n.next;
36.  
    //1、b的后继节点两次读取不一致，重试
37.  
    if (n != b.next) // inconsistent read
38.  
    break;
39.  
    Object v = n.value;

1.  
   //2、数据节点的值为null，表示该数据节点标记为已删除，移除该数据节点并重试。
2.  
   if (v == null) { // n is deleted
3.  
   n.helpDelete(b, f);
4.  
   break;
5.  
   }
6.  
   //3、b节点被标记为删除，重试
7.  
   if (v == n || b.value == null) // b is deleted
8.  
   break;
9.  
   int c = key.compareTo(n.key);
10.  
    if (c == 0)//找到返回
11.  
    return n;
12.  
    if (c < 0)//给定key小于当前可以，不存在
13.  
    return null;
14.  
    b = n;//否则继续查找
15.  
    n = f;
16.  
    }
17.  
    }
18.  
    }

1.  
   /**Returns a base-level node with key strictly less than given key, or the base-level header if there is no such node.
2.  
   Also unlinks indexes to deleted nodes found along the way. Callers rely on this side-effect of clearing indices to deleted nodes.
3.  
   * @param key the key
4.  
   * @return a predecessor of key */
5.  
   //返回“小于且最接近给定key”的数据节点，如果不存在这样的数据节点就返回最低级别的索引头。
6.  
   private Node<K,V> findPredecessor(Comparable<? super K> key) {
7.  
   if (key == null)
8.  
   throw new NullPointerException(); // don't postpone errors
9.  
   for (;;) {
10.  
    Index<K,V> q = head;//从顶层索引开始查找
11.  
    Index<K,V> r = q.right;
12.  
    for (;;) {
13.  
    if (r != null) {
14.  
    Node<K,V> n = r.node;
15.  
    K k = n.key;
16.  
    if (n.value == null) {//数据节点的值为null,表示该数据节点标记为已删除，断开连接并重试
17.  
    if (!q.unlink(r))
18.  
    break; // restart
19.  
    r = q.right; // reread r
20.  
    continue;
21.  
    }
22.  
    if (key.compareTo(k) > 0) {//给定key大于当前key，继续往右查找
23.  
    q = r;
24.  
    r = r.right;
25.  
    continue;
26.  
    }
27.  
    }
28.  
    //执行到这里有两种情况：
29.  
    //1、当前级别的索引查找结束
30.  
    //2、给定key小于等于当前key
31.  
    Index<K,V> d = q.down;//在下一级别索引中查找
32.  
    if (d != null) {//如果还存在更低级别的索引，在更低级别的索引中继续查找
33.  
    q = d;
34.  
    r = d.right;
35.  
    } else
36.  
    return q.node;//如果当前已经是最低级别的索引，当前索引节点关联的数据节点即为所求
37.  
    }
38.  
    }
39.  
    }

插入

1.  
   /**
2.  
   * Associates the specified value with the specified key in this map.
3.  
   * If the map previously contained a mapping for the key, the old value is replaced.
4.  
   *
5.  
   * @param key key with which the specified value is to be associated
6.  
   * @param value value to be associated with the specified key
7.  
   * @return the previous value associated with the specified key, or
8.  
   * <tt>null</tt> if there was no mapping for the key
9.  
   * @throws ClassCastException if the specified key cannot be compared
10.  
    * with the keys currently in the map
11.  
    * @throws NullPointerException if the specified key or value is null
12.  
    */
13.  
    public V put(K key, V value) {
14.  
    if (value == null)
15.  
    throw new NullPointerException();
16.  
    return doPut(key, value, false);
17.  
    }

1.  
   /**
2.  
   * Main insertion method. Adds element if not present, or replaces value if present and onlyIfAbsent is false.
3.  
   * @param kkey the key
4.  
   * @param value the value that must be associated with key
5.  
   * @param onlyIfAbsent if should not insert if already present
6.  
   * @return the old value, or null if newly inserted
7.  
   */
8.  
   private V doPut(K kkey, V value, boolean onlyIfAbsent) {
9.  
   Comparable<? super K> key = comparable(kkey);
10.  
    for (;;) {
11.  
    Node<K,V> b = findPredecessor(key);//查找前驱数据节点
12.  
    Node<K,V> n = b.next;
13.  
    for (;;) {
14.  
    if (n != null) {
15.  
    Node<K,V> f = n.next;
16.  
    //1、b的后继两次读取不一致，重试
17.  
    if (n != b.next) // inconsistent read
18.  
    break;
19.  
    Object v = n.value;
20.  
    //2、数据节点的值为null,表示该数据节点标记为已删除，移除该数据节点并重试。
21.  
    if (v == null) { // n is deleted
22.  
    n.helpDelete(b, f);
23.  
    break;
24.  
    }
25.  
    //3、b节点被标记为已删除，重试
26.  
    if (v == n || b.value == null) // b is deleted
27.  
    break;
28.  
    int c = key.compareTo(n.key);
29.  
    if (c > 0) {//给定key大于当前可以，继续寻找合适的插入点
30.  
    b = n;
31.  
    n = f;
32.  
    continue;
33.  
    }
34.  
    if (c == 0) {//找到
35.  
    if (onlyIfAbsent || n.casValue(v, value))
36.  
    return (V)v;
37.  
    else
38.  
    break; // restart if lost race to replace value
39.  
    }
40.  
    // else c < 0; fall through
41.  
    }
42.  
    //没有找到，新建数据节点
43.  
    Node<K,V> z = new Node<K,V>(kkey, value, n);
44.  
    if (!b.casNext(n, z))
45.  
    break; // restart if lost race to append to b
46.  
    int level = randomLevel();//随机的索引级别
47.  
    if (level > 0)
48.  
    insertIndex(z, level);
49.  
    return null;
50.  
    }
51.  
    }
52.  
    }

1.  
   /**
2.  
   * Creates and adds index nodes for the given node.
3.  
   * @param z the node
4.  
   * @param level the level of the index
5.  
   */
6.  
   private void insertIndex(Node<K,V> z, int level) {
7.  
   HeadIndex<K,V> h = head;
8.  
   int max = h.level;
9.  
    
10.  
    if (level <= max) {//索引级别已经存在，在当前索引级别以及底层索引级别上都添加该节点的索引
11.  
    Index<K,V> idx = null;
12.  
    for (int i = 1; i <= level; ++i)//首先得到一个包含1~level个索引级别的down关系的链表，最后的inx为最高level索引 
13.  
    idx = new Index<K,V>(z, idx, null);
14.  
    addIndex(idx, h, level);//Adds given index nodes from given level down to 1.新增索引
15.  
    } else { // Add a new level 新增索引级别
16.  
    /* To reduce interference by other threads checking for empty levels in tryReduceLevel, new levels are added
17.  
    * with initialized right pointers. Which in turn requires keeping levels in an array to access them while
18.  
    * creating new head index nodes from the opposite direction. */
19.  
    level = max + 1;
20.  
    Index<K,V>[] idxs = (Index<K,V>[])new Index[level+1];
21.  
    Index<K,V> idx = null;
22.  
    for (int i = 1; i <= level; ++i)
23.  
    idxs[i] = idx = new Index<K,V>(z, idx, null);
24.  
     
25.  
    HeadIndex<K,V> oldh;
26.  
    int k;
27.  
    for (;;) {
28.  
    oldh = head;
29.  
    int oldLevel = oldh.level;//更新head
30.  
    if (level <= oldLevel) { // lost race to add level
31.  
    k = level;
32.  
    break;
33.  
    }
34.  
    HeadIndex<K,V> newh = oldh;
35.  
    Node<K,V> oldbase = oldh.node;
36.  
    for (int j = oldLevel+1; j <= level; ++j)
37.  
    newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);
38.  
    if (casHead(oldh, newh)) {
39.  
    k = oldLevel;
40.  
    break;
41.  
    }
42.  
    }
43.  
    addIndex(idxs[k], oldh, k);
44.  
    }
45.  
    }

参考：

JDK 1.7源码

http://blog.csdn.net/ict2014/article/details/17394259

http://blog.sina.com.cn/s/blog_72995dcc01017w1t.html

https://yq.aliyun.com/articles/38381

http://www.2cto.com/kf/201212/175026.html

http://ifeve.com/cas-skiplist/