spark 机器学习 决策树 原理(一)

1.什么是决策树　　
决策树（decision tree）是一个树结构（可以是二叉树或者非二叉树）。决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。
　　其中每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放在一个类别。
　　使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，知道到达叶子节点，将叶子节点存放的类别作为决策结果。
决策树学习算法主要由三部分构成

1.1特征选择
　　特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准，从而衍生出不同的决策树算法。
1.2决策树生成
　　根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。树结构来说，递归结构是最容易理解的方式。
1.3决策树的剪枝
决策树容易过拟合，一般来需要剪枝，缩小树结构规则，缓解过拟合，剪枝技术有预剪枝和后剪枝两种。

2.例子
一天，老师问了个问题，只根据头发和声音怎么判断一位同学的性别。
为了解决这个问题，同学们马上简单的统计了7位同学的相关特征，数据如下：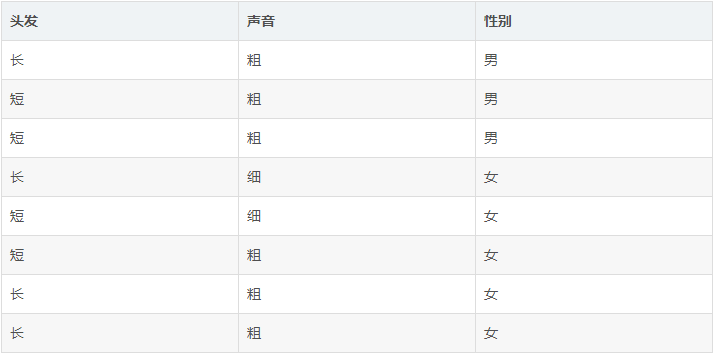

同学A想了想，先根据头发判断，若判断不出，再根据声音判断，于是画了一幅图，如下：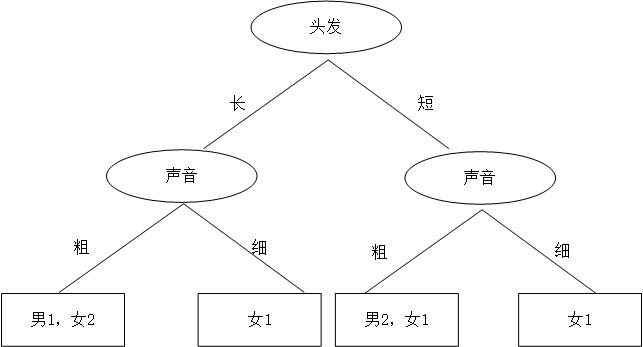

同学B，想先根据声音判断，然后再根据头发来判断，如是大手一挥也画了个决策树：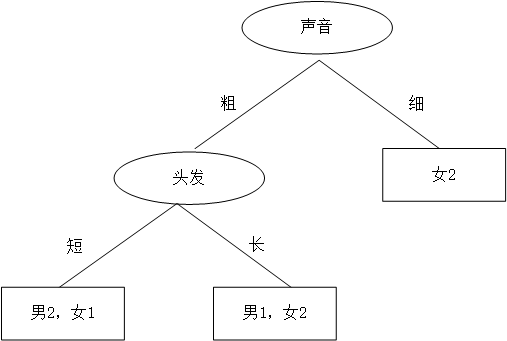

同学A和同学B谁的决策树好些？

3.决策树的特征选择
我们可以使用多种方法划分数据集，但是每种方法都有各自的优缺点。于是我们这么想，如果我们能测量数据的复杂度，对比按不同特征分类后的数据复杂度，若按某一特征分类后复杂度减少的更多，那么这个特征即为最佳分类特征。
Claude Shannon 定义了熵（entropy）和信息增益(information gain)。
3.1信息熵
首先了解一下信息量：信息量是对信息的度量，就跟时间的度量是秒一样，当我们考虑一个离散的随机变量 x 的时候，当我们观察到的这个变量的一个具体值的时候，我们接收到了多少信息呢？
信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大，如中国足球队勇夺世界杯冠军，越大概率的事情发生了产生的信息量越小，如太阳从东边升起来了（肯定发生嘛， 没什么信息量）。

在信息论与概率论中，熵（entropy）用于表示“随机变量不确定性的度量”

X代表样本总数据量，n代表结果分类，p(xi)代表xi的概率(就是结果其中一个分类的概率):
例子：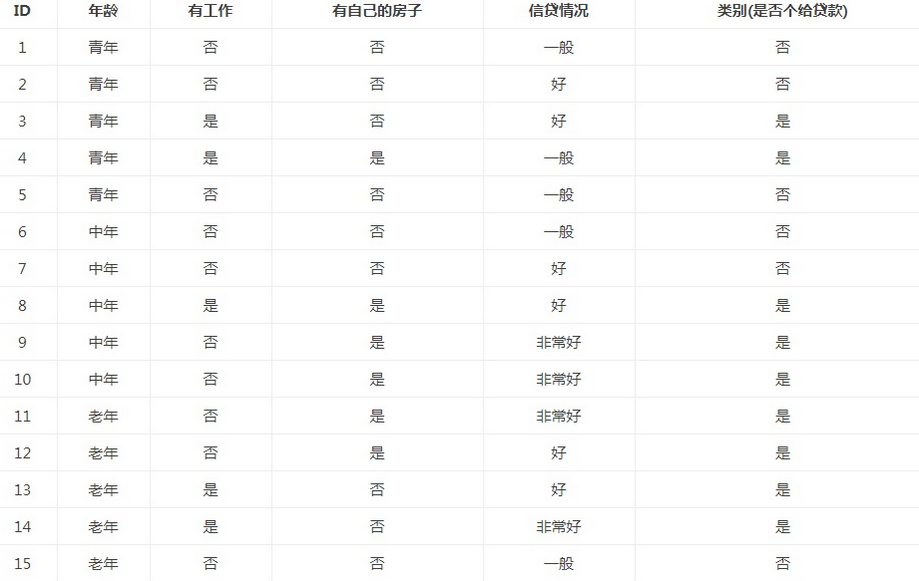

在15个数据中，结果分类为2个，放贷或不放贷，9个数据的结果为放贷，6个数据的结果为不放贷。所以数据集X的信息熵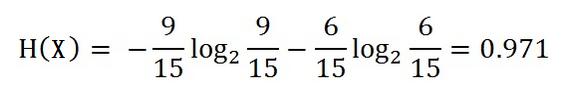

3.2信息增益（information gain）
 我们已经说过，如何选择特征，需要看信息增益。也就是说，信息增益是相对于特征而言的，信息增益越大，特征对最终的分类结果影响也就越大，我们就应该选择对最终分类结果影响最大的那个特征作为我们的分类特征。
在讲解信息增益定义之前，我们还需要明确一个概念，条件熵。

接下来，让我们说说信息增益。前面也提到了，信息增益是相对于特征而言的。所以，特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：

以贷款申请样本数据表为例进行说明。看下年龄这一列的数据，也就是特征A1，一共有三个类别，分别是：青年、中年和老年。我们只看年龄是青年的数据，年龄是青年的数据一共有5个，所以年龄是青年的数据在训练数据集出现的概率是十五分之五，也就是三分之一。同理，年龄是中年和老年的数据在训练数据集出现的概率也都是三分之一。现在我们只看年龄是青年的数据的最终得到贷款的概率为五分之二，因为在五个数据中，只有两个数据显示拿到了最终的贷款，同理，年龄是中年和老年的数据最终得到贷款的概率分别为五分之三、五分之四。所以计算年龄的信息增益，过程如下：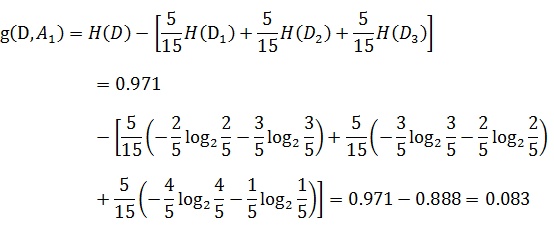

同理，计算其余特征的信息增益g(D,A2)、g(D,A3)和g(D,A4)。分别为：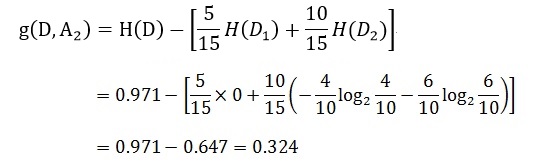

最后，比较特征的信息增益，由于特征A3(有自己的房子)的信息增益值最大，所以选择A3作为最优特征。