逆向破解之160个CrackMe —— 021

CrackMe —— 021

160 CrackMe 是比较适合新手学习逆向破解的CrackMe的一个集合一共160个待逆向破解的程序

CrackMe:它们都是一些公开给别人尝试破解的小程序，制作 crackme 的人可能是程序员，想测试一下自己的软件保护技术，也可能是一位 cracker，想挑战一下其它 cracker 的破解实力，也可能是一些正在学习破解的人，自己编一些小程序给自己破。

CrackMe简称CM。

程序下载地址：点击我

来源 <-点击查看

编号	作者	保护方式
021	Cabeca	Name/Serial1/Serial2(Delphi)

工具

x32dbg

VB Decompiler Pro

开始破解之旅

ON.1

爆破方式

我们首先使用VB Decompiler Pro 打开021号程序，点击Procedures ->Events 我们在下方窗口内看见两个事件函数，一个是输入触发的事件一个是按钮点击的事件

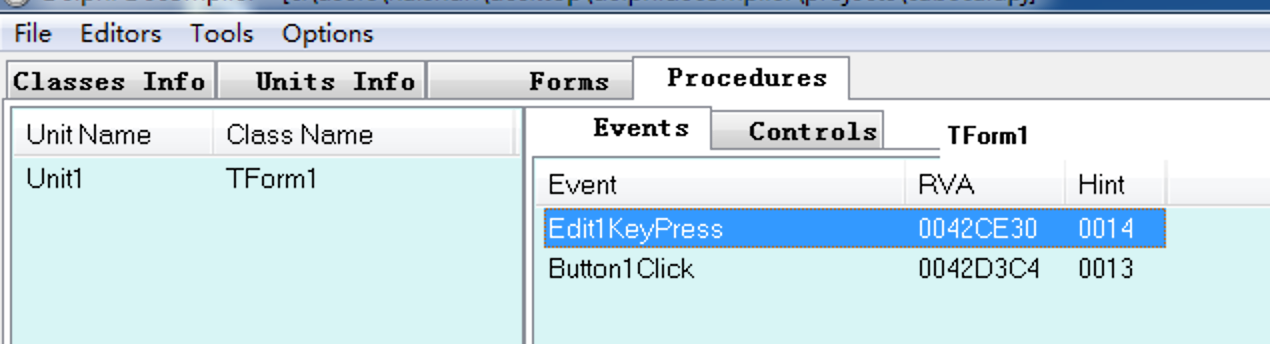
我们记下按钮点击事件的地址0042D3C4

使用x32dbg打开程序在004D3C4处下断，在程序输入框内输入任意数据，点击按钮，程序停在了断点处

单步F8向下运行

此时我们停在了0042D4AA处，看到程序跳过正确提示符处，我们将0042D4AA处JNE修改为NOP继续单步向下

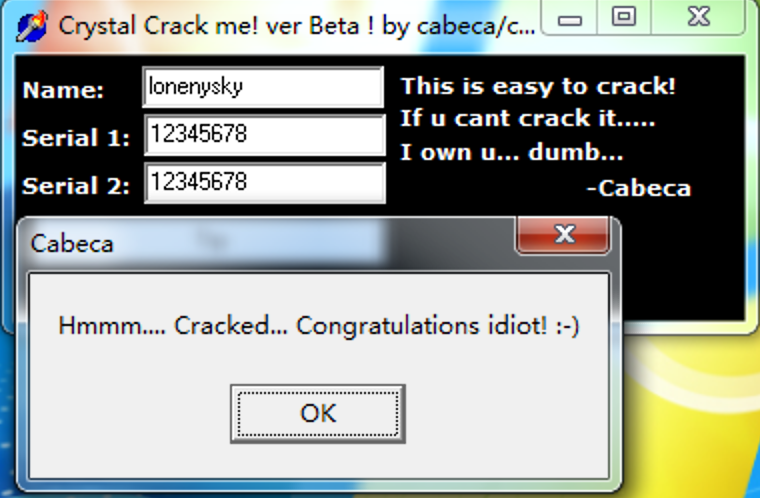
继续单步向下来到了下一个跳转处，看到红色的线跳过了正确提示处，我们将0042D4D4处JNE修改为NOP，F9运行

bingo ~ 破解成功

ON.2

追码方式

我们在窗口内输入以下数据

Name : lonenysky

Serial 1 : 1234567

Serial 2 : 1234567

在之前的按钮事件处下断，下断后点击Try按钮，F8单步向下

当我们经过0042D48A地址处时，计算出一个字符串，该字符串疑似第一个注册码

0042D480 |                      | je cabeca.42D4E5                                        |
0042D482 | 8D55 F0                  | lea edx,dword ptr ss:[ebp-0x10]                         | [ebp-]:""
0042D485 | A1 14F74200              | mov eax,dword ptr ds:[0x42F714]                         |
0042D48A | E8 C190FDFF              | call <cabeca.sub_406550>                                |
0042D48F | 8B45 F0                  | mov eax,dword ptr ss:[ebp-0x10]                         | [ebp-]:""
0042D492 |                        | push eax                                                |
0042D493 | 8D55 FC                  | lea edx,dword ptr ss:[ebp-0x4]                          | [ebp-]:"lonenysky"
0042D496 | 8B83 E4010000            | mov eax,dword ptr ds:[ebx+0x1E4]                        |
0042D49C | E8 3FC9FEFF              | call <cabeca.sub_419DE0>                                |
0042D4A1 | 8B55 FC                  | mov edx,dword ptr ss:[ebp-0x4]                          | [ebp-]:"lonenysky"
0042D4A4 |                        | pop eax                                                 |
0042D4A5 | E8 2664FDFF              | call <cabeca.sub_4038D0>                                |
0042D4AA |                      | jne cabeca.42D4E5                                       |
0042D4AC | 8D55 F0                  | lea edx,dword ptr ss:[ebp-0x10]                         | [ebp-]:""
0042D4AF | A1 18F74200              | mov eax,dword ptr ds:[0x42F718]                         |
0042D4B4 | E8 9790FDFF              | call <cabeca.sub_406550>                                |
0042D4B9 | 8B45 F0                  | mov eax,dword ptr ss:[ebp-0x10]                         | [ebp-]:""
0042D4BC |                        | push eax                                                |
0042D4BD | 8D55 FC                  | lea edx,dword ptr ss:[ebp-0x4]                          | [ebp-]:"lonenysky"
0042D4C0 | 8B83 EC010000            | mov eax,dword ptr ds:[ebx+0x1EC]                        |

0042D48A处Call为计算Serial 1的函数

我们将Serial 1处的输入框的内容改为，再次点击Try按钮F8单步向下

此时经过0042D4A4地址处时没有发生跳转，说明Serial 1注册码正确，注册码为

继续F8向下

此时我们看到在进入0042D4C6地址后计算出一个新的字符串疑似我们的Serial 2注册码

0042D4C6 | E8 15C9FEFF              | call <cabeca.sub_419DE0>                                |
0042D4CB | 8B55 FC                  | mov edx,dword ptr ss:[ebp-0x4]                          | [ebp-]:""
0042D4CE |                        | pop eax                                                 | eax:""
0042D4CF | E8 FC63FDFF              | call <cabeca.sub_4038D0>                                |
0042D4D4 |  0F                    | jne cabeca.42D4E5                                       |
0042D4D6 | B8 E8D54200              | mov eax,cabeca.42D5E8                                   | eax:"", 42D5E8:"Hmmm.... Cracked... Congratulations idiot! :-)"

将Serial 2输入框内修改为8327，确定

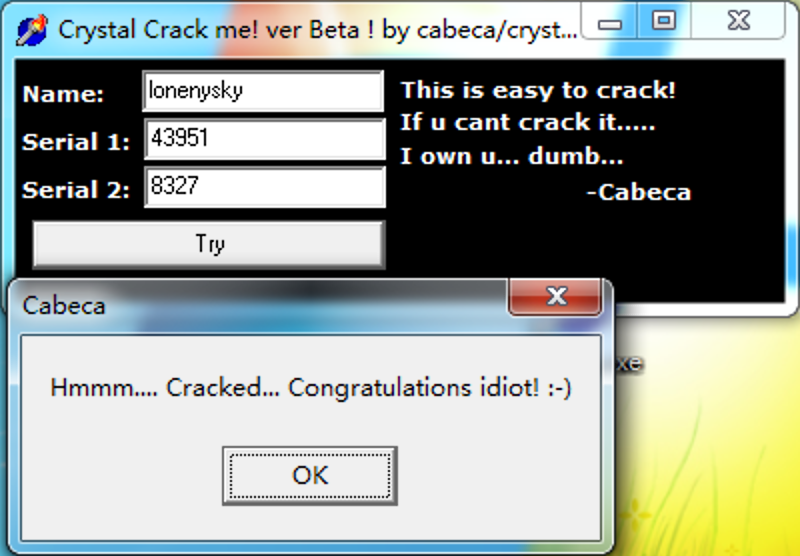
bingo ~ 破解成功