图论 - Bellman-Ford算法

Bellman-Ford

Dijkstra算法虽好，但是不能解决带有负边权的图.

而利用Bellman-Ford可以完美的解决最短路和负边权的问题

朴素Bellman-Ford算法

w[i] 权值

u[i]->v[i] 存储边集

默认大家已经会了邻接表存储，如果有没有学会邻接表存储的小伙伴要先去学习一些邻接表的存储操作哦! ^_

核心代码:

for(int k = 1; k <= n-1; k++)
   for(int i = 1; i <= m; i++)
      if(dis[v[i]] > dis[u[i]] + w[i])
         dis[v[i]] = dis[u[i]] + w[i];

显然其时间复杂度为O(m*n)

分析过程

下面列出一个具体的松弛过程可帮助大家更好的理解代码:

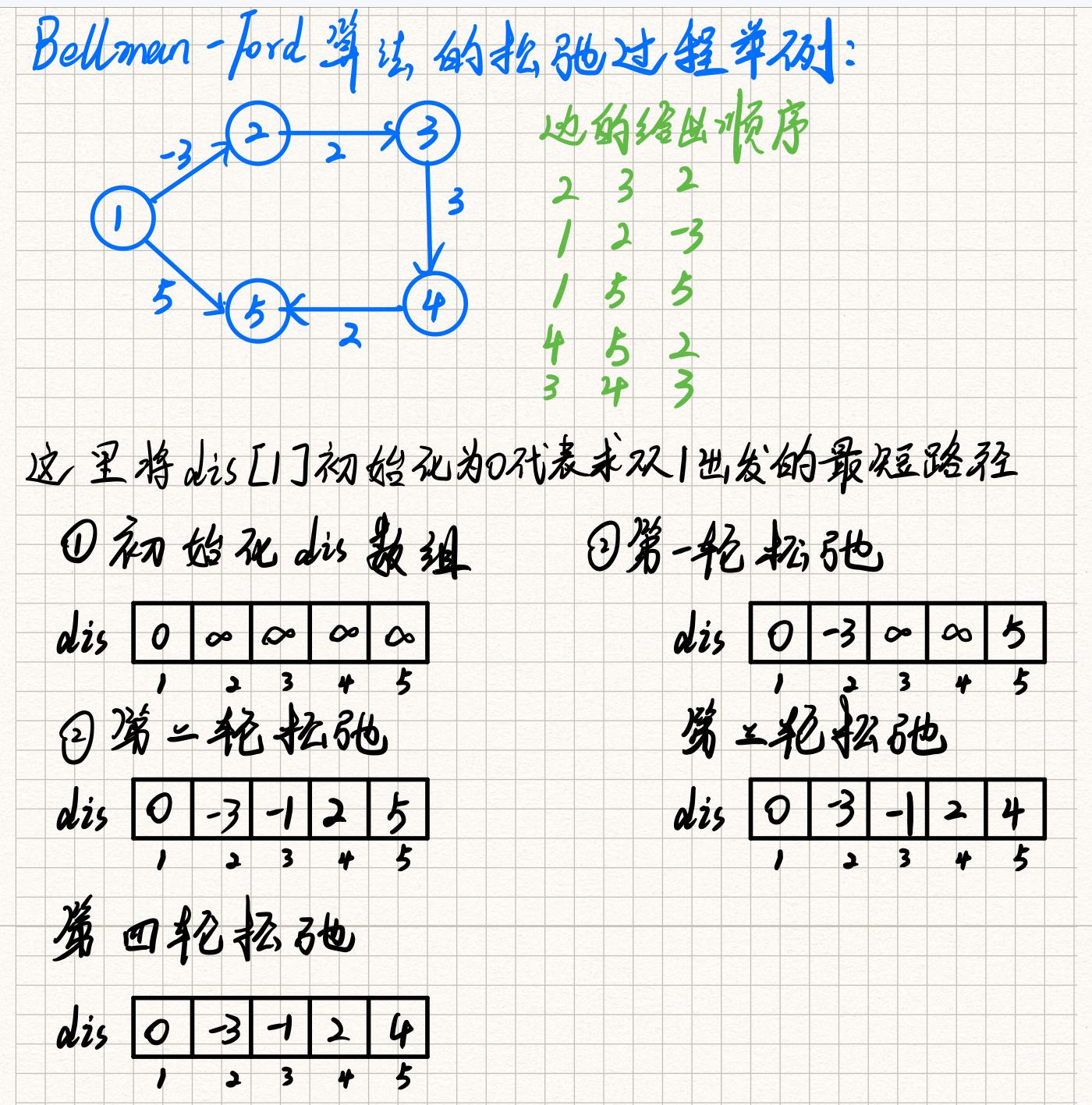
完整代码:

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
	int dis[10], n, m, u[10], v[10], w[10];
	int inf = 9999999;
	cin >> n >> m;
	//读入边
	for (int i = 1; i <= m; i++)
		cin >> u[i] >> v[i] >> w[i];
	//初始化dis数组
	fill(dis, dis + 10, inf);
	dis[1] = 0;//由于要求的是从1->任意一个点的最短距离所以将1的dis设置为0
	//Bellman-Ford核心算法
	for (int i = 0; i < n - 1; i++)
		for (int j = 1; j <= m; j++)
			if (dis[v[j]] > dis[u[j]] + w[j])
				dis[v[j]] = dis[u[j]] + w[j];
	//输出结果
	for (int i = 1; i <= n; i++)
		cout << dis[i] << " ";
	system("pause");
	return 0;
}

如果大家有什么疑问的话可以加qq向我提出哦,欢迎各位大佬指出问题。

如果你觉得对你有所帮助的话就给我点个赞,点燃我下次写文章的动力吧 ^_ !