HDU 5073 Galaxy (2014 Anshan D简单数学)
HDU 5073 Galaxy (2014 Anshan D简单数学)
题目链接http://acm.hdu.edu.cn/showproblem.php?pid=5073
Description
Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present. To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula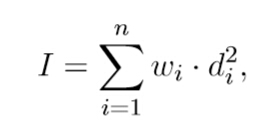
where wi is the weight of star i, di is the distance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.
Now, you are supposed to calculate the minimum moment of inertia after transportation.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.
Output
For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2
Sample Output
0
0.5
题意:
给你n个在x轴点,其中k个可以任意变换坐标点,问此时每个点距离质心的距离平方和最小是多少?
题解:
首先将所有的点排序。然后每次o(n)扫描一遍。首先我们知道质心是每个坐标的和的平均值。那么从头到尾扫描每次删除起始点,添加最后点的下一个点。我们只需将这个公式拆开即可化简。注意n==k的时候输出0
代码:
#include <bits/stdc++.h>
const int N = 100005 ;
double pos[N] ;
int main()
{
int t ;
scanf("%d",&t) ;
while(t--){
int n , k ;
scanf("%d %d",&n,&k) ;
for(int i = 1 ; i <= n ; i ++){
scanf("%lf",pos+i) ;
}
if(n == k){
printf("0\n") ;
continue ;
}
std::sort(pos+1,pos+1+n) ;
double sum = 0 ;
double psum = 0 ;
for(int i = 1 ; i <= n-k ; i ++){
sum += pos[i] ;
psum += pos[i]*pos[i] ;
}
double avg = sum/(n-k) ;
double ans = psum + (n-k)*avg*avg - 2*avg*sum ;
for(int i = 1 ; i <= k ; i ++){
sum -= pos[i] ;
sum += pos[n-k+i] ;
psum -= pos[i]*pos[i] ;
psum += pos[n-k+i]*pos[n-k+i] ;
avg = sum/(n-k) ;
double temp = psum + (n-k)*avg*avg - 2*avg*sum ;
ans = std::min(ans,temp) ;
}
printf("%.10lf\n",ans) ;
}
return 0 ;
}
HDU 5073 Galaxy (2014 Anshan D简单数学)的更多相关文章
- HDU 5073 Galaxy(Anshan 2014)(数学推导,贪婪)
Galaxy Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others) Total S ...
- HDU 5073 Galaxy 2014 Asia AnShan Regional Contest 规律题
推公式 #include <cstdio> #include <cmath> #include <iomanip> #include <iostream> ...
- HDU 5073 Galaxy(2014鞍山赛区现场赛D题)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5073 解题报告:在一条直线上有n颗星星,一开始这n颗星星绕着重心转,现在我们可以把其中的任意k颗星星移 ...
- hdu 5073 Galaxy(2014acm鞍山亚洲分部 C)
主题链接:http://acm.hdu.edu.cn/showproblem.php? pid=5073 Galaxy Time Limit: 2000/1000 MS (Java/Others) ...
- hdu 5073 Galaxy(2014acm鞍山亚洲分部 D)
主题链接:http://acm.hdu.edu.cn/showproblem.php? pid=5073 Galaxy Time Limit: 2000/1000 MS (Java/Others) ...
- 2014 Asia AnShan Regional Contest --- HDU 5073 Galaxy
Galaxy Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=5073 Mean: 在一条数轴上,有n颗卫星,现在你可以改变k颗 ...
- hdu 5073 Galaxy(2014 鞍山现场赛)
Galaxy Time Limit: 2000/1000 MS (J ...
- ACM学习历程—HDU 5073 Galaxy(数学)
Description Good news for us: to release the financial pressure, the government started selling gala ...
- hdu 5073 Galaxy 数学 铜牌题
0.5 题意:有n(n<=5e4)个质点位于一维直线上,现在你可以任意移动其中k个质点,且移动到任意位置,设移动后的中心为e,求最小的I=(x[1]-e)^2+(x[2]-e)^2+(x[3]- ...
随机推荐
- IP选路
IP选路 1.概述 路由算法是用于获取路由表中的路由项目.它是路由选择协议的核心. 2.路由算法的分类 从路由算法能否随网络的通信量或拓扑自适应的进行调整变化来分,可以分为两类. ...
- Windows应用商店API
Windows应用商店API 动手实验 实验 8: Windows应用商店API 2012年9月 简介 编写Windows应用商店应用最令人瞩目的理由之一是您可以方便地将它们发布到Windows应用商 ...
- 使用Android网络编程实现简易聊天室
在Java中我们可以利用socket编程实现聊天室,在Android中也一样,因为Android完全支持JDK本身的TCP.UDP网络通信API.我们可以使用ServerSocket.Socket来建 ...
- JSP引擎的工作原理
JSP运行环境: 执行JSP代码需要在服务器上安装JSP引擎,比较常见的引擎有WebLogic和Tomcat.把这些支持JSP的web服务器配置好后.就可以再客户端通过浏览器来访问JSP页面了.默认端 ...
- 项目开发之分页---异步分页(ajax)
PS:前面忘了给大家讲解后台需要做的 ,同步分页的时候,我们只需要定义一个方法,给前台传递一个page对象,前台接收到直接展示即可:异步分页要多一步,首先还是写一个方法,传递初始对象,后面的ajax返 ...
- C#开发学习——web服务器端控件
Asp.net在客户端开发和web开发所用到的控件还是有很大的差别的,而且Web开发的界面是在浏览器中显示的,所以控件的设计都和前边学习HTML设计有联系,没有客户端开发那么简单,不过我们可以 ...
- Android JDK配置使支持Gradle更新,Maven安装
配置Maven 或执行Gradle更新等相关命令时出现以下错误时要重新配置JDK ERROR: JAVA_HOME is set to an invalid directory.JAVA_HOME = ...
- Python json解析
#encoding: utf-8 ''' Author:Siukwan ''' import sys reload(sys) sys.setdefaultencoding('utf8') import ...
- BHuman文档结构
Chapter 2 : a short introduction how to build the code including the required software and how to ru ...
- String.split()分割字符串
string.split(s[, sep[, maxsplit]]) Return a list of the words of the string s. If the optional secon ...
题目链接http://acm.hdu.edu.cn/showproblem.php?pid=5073
Description
Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.
To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.
Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.
The moment of inertia I of a set of n stars can be calculated with the formula
where wi is the weight of star i, di is the distance form star i to the mass of center.
As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.
Now, you are supposed to calculate the minimum moment of inertia after transportation.
Input
The first line contains an integer T (T ≤ 10), denoting the number of the test cases.
For each test case, the first line contains two integers, n(1 ≤ n ≤ 50000) and k(0 ≤ k ≤ n), as mentioned above. The next line contains n integers representing the positions of the stars. The absolute values of positions will be no more than 50000.
Output
For each test case, output one real number in one line representing the minimum moment of inertia. Your answer will be considered correct if and only if its absolute or relative error is less than 1e-9.
Sample Input
2
3 2
-1 0 1
4 2
-2 -1 1 2
Sample Output
0
0.5
题意:
给你n个在x轴点,其中k个可以任意变换坐标点,问此时每个点距离质心的距离平方和最小是多少?
题解:
首先将所有的点排序。然后每次o(n)扫描一遍。首先我们知道质心是每个坐标的和的平均值。那么从头到尾扫描每次删除起始点,添加最后点的下一个点。我们只需将这个公式拆开即可化简。注意n==k的时候输出0
代码:
#include <bits/stdc++.h>
const int N = 100005 ;
double pos[N] ;
int main()
{
int t ;
scanf("%d",&t) ;
while(t--){
int n , k ;
scanf("%d %d",&n,&k) ;
for(int i = 1 ; i <= n ; i ++){
scanf("%lf",pos+i) ;
}
if(n == k){
printf("0\n") ;
continue ;
}
std::sort(pos+1,pos+1+n) ;
double sum = 0 ;
double psum = 0 ;
for(int i = 1 ; i <= n-k ; i ++){
sum += pos[i] ;
psum += pos[i]*pos[i] ;
}
double avg = sum/(n-k) ;
double ans = psum + (n-k)*avg*avg - 2*avg*sum ;
for(int i = 1 ; i <= k ; i ++){
sum -= pos[i] ;
sum += pos[n-k+i] ;
psum -= pos[i]*pos[i] ;
psum += pos[n-k+i]*pos[n-k+i] ;
avg = sum/(n-k) ;
double temp = psum + (n-k)*avg*avg - 2*avg*sum ;
ans = std::min(ans,temp) ;
}
printf("%.10lf\n",ans) ;
}
return 0 ;
}
Galaxy Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others) Total S ...
推公式 #include <cstdio> #include <cmath> #include <iomanip> #include <iostream> ...
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5073 解题报告:在一条直线上有n颗星星,一开始这n颗星星绕着重心转,现在我们可以把其中的任意k颗星星移 ...
主题链接:http://acm.hdu.edu.cn/showproblem.php? pid=5073 Galaxy Time Limit: 2000/1000 MS (Java/Others) ...
主题链接:http://acm.hdu.edu.cn/showproblem.php? pid=5073 Galaxy Time Limit: 2000/1000 MS (Java/Others) ...
Galaxy Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=5073 Mean: 在一条数轴上,有n颗卫星,现在你可以改变k颗 ...
Galaxy Time Limit: 2000/1000 MS (J ...
Description Good news for us: to release the financial pressure, the government started selling gala ...
0.5 题意:有n(n<=5e4)个质点位于一维直线上,现在你可以任意移动其中k个质点,且移动到任意位置,设移动后的中心为e,求最小的I=(x[1]-e)^2+(x[2]-e)^2+(x[3]- ...
IP选路 1.概述 路由算法是用于获取路由表中的路由项目.它是路由选择协议的核心. 2.路由算法的分类 从路由算法能否随网络的通信量或拓扑自适应的进行调整变化来分,可以分为两类. ...
Windows应用商店API 动手实验 实验 8: Windows应用商店API 2012年9月 简介 编写Windows应用商店应用最令人瞩目的理由之一是您可以方便地将它们发布到Windows应用商 ...
在Java中我们可以利用socket编程实现聊天室,在Android中也一样,因为Android完全支持JDK本身的TCP.UDP网络通信API.我们可以使用ServerSocket.Socket来建 ...
JSP运行环境: 执行JSP代码需要在服务器上安装JSP引擎,比较常见的引擎有WebLogic和Tomcat.把这些支持JSP的web服务器配置好后.就可以再客户端通过浏览器来访问JSP页面了.默认端 ...
PS:前面忘了给大家讲解后台需要做的 ,同步分页的时候,我们只需要定义一个方法,给前台传递一个page对象,前台接收到直接展示即可:异步分页要多一步,首先还是写一个方法,传递初始对象,后面的ajax返 ...
Asp.net在客户端开发和web开发所用到的控件还是有很大的差别的,而且Web开发的界面是在浏览器中显示的,所以控件的设计都和前边学习HTML设计有联系,没有客户端开发那么简单,不过我们可以 ...
配置Maven 或执行Gradle更新等相关命令时出现以下错误时要重新配置JDK ERROR: JAVA_HOME is set to an invalid directory.JAVA_HOME = ...
#encoding: utf-8 ''' Author:Siukwan ''' import sys reload(sys) sys.setdefaultencoding('utf8') import ...
Chapter 2 : a short introduction how to build the code including the required software and how to ru ...
string.split(s[, sep[, maxsplit]]) Return a list of the words of the string s. If the optional secon ...
