数据结构中的棧在C#中的实现

数据结构中的棧在C#中的实现

一、大致学习

棧是一种面向表的数据结构，棧中的数据只能在标的某一短进行添加和删除操作，是一种典型的（LIFO）数据结构。

现实生活中的理解：自助餐厅的盘子堆，人们总是从顶部取走盘子，当洗碗工把洗好的盘子放回盘子堆的时候也是放在盘子堆的顶部。

Stack类实现棧：Stack<T> number=new Stack<T>();

Stack类是ICollection接口的一个实现(foreach)，它代表了一个LIFO群集或一个棧，在.NET中作为循环缓冲来实现的，这使得能动态地分配进栈数据项的空间；

Stack构造器方法，默认的构造器实例化的是一个具有10个数值初始容量的空栈，每当棧达到满容量时就会把容量值翻倍；另一种构造器允许创建一个来自另一个群集对象的棧对象

如：

string [] names= new string[]{"jack","rose","jeff"};
 
Stack nameStack=new Stack(names);

二、具体分析

C#Stack泛型类的常用方法介绍：

1、Push(object item)方法：将对象插入栈顶，同时将棧的初始变量+1

 public void Push(object item)
 {
       list.Add(item);
        p_index++;
  }

2、Pop()方法：将对象移除栈顶，同时将棧的初始变量-1，返回出棧的对象

 public object Pop()
 {
       object obj=list[p_index];
       list.RemoveAt(p_index);
       p_index--;
       return obj;
}

3、Peek()方法：取数，只是查看栈顶元素的”值“

       public object Peek()
        {
            return list[p_index];
        }

4、Clear()方法：清空棧内数据，将数据项计数器设置为0

        public void Clear()
        {
            list.Clear();
            p_index = -1;
        }

5、Contains()方法：用来确定指定的元素是否在棧内 bool

        public bool Contains(object item)
        {
            return list.Contains(item);
        }

6、CopyTo()方法：将棧内的内容复制到一个数组中，要求数组必须是object类型的，因为这是所有棧对象的数据类型。包含两个参数：一个数组和起始索引值

Stack myStack=new Stack();
for(int i=20;i>0;i--)
{
    myStack.Push(i);
}
object [] myArray=new object[myStack.Count];
myStack.CopyTo(myArray,0);

7、ToArray()方法：复制到一个新的数组中，不含索引值，故需创建新的数组

Stack myStack=new Stack();
for(int i=0;i>0;i++)
{
    myStack.Push(i);
}
object [] myArray=new object[myStack.Count];
myArray=myStack.ToArray();

8、Count属性：获取棧中的元素个数

public int Count
{
     get
     {
           return list.Count;
      }
}

三、案例分析

1、使用棧来判断回文

把相同的词汇或句子，在下文中调换位置或颠倒过来，产生首尾回环的情趣，叫做回文，也叫回环。

class CStack
    {
        private int p_index;
        private ArrayList list;
        public CStack()
        {
            list = new ArrayList();
            p_index = -1;
        }
        //获取棧的空间
        public int Count
        {
            get
            {
                return list.Count;
            }
        }
        //进栈
        public void Push(object item)
        {
            list.Add(item);
            p_index++;
        }
        //出棧
        public object Pop()
        {
            object obj=list[p_index];
            list.RemoveAt(p_index);
            p_index--;
            return obj;
        }
        //清空棧内元素
        public void Clear()
        {
            list.Clear();
            p_index = -1;
        }
        //取数
        public object Peek()
        {
            return list[p_index];
        }
        public bool Contains(object item)
        {
            return list.Contains(item);
        }
    }

static void Main(string[] args)
        {
            CStack alist = new CStack();
            string ch;
            string word = "woainiiniaow";
            bool isPalindrome = true;
            //将word反转存入棧中
            for (int i = 0; i < word.Length;i++ )
            {
                alist.Push(word.Substring(i,1));
            }
            //进行判断
            int pos = 0;
            while(alist.Count>0)
            {
                ch = alist.Pop().ToString();
                if (ch != word.Substring(pos, 1))
                {
                    isPalindrome = false;
                    break;
                }
                else
                {
                    pos++;
                }
            }
            if (isPalindrome)
            {
                Console.WriteLine("{0}是回文", word);
            }
            else
            {
                Console.WriteLine("{0}不是回文", word);
            }
            Console.ReadKey();
        } //另外我觉得可采用另一种常规方法就是复制一个“数组”，原“数组”从0->Length遍历，新“数组”从Length->0遍历，进行比对。

2、使用棧来实现四则运算

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Text.RegularExpressions;
using System.Collections;
 
namespace _09使用棧来实现四则运算
{
    class Program
    {
        static void Main(string[] args)
        {
            Stack nums = new Stack();
            Stack ops = new Stack();
            string expression = "5*2";
            Calculate(nums,ops,expression);
            Console.WriteLine(nums.Pop());
            Console.ReadKey();
        }
        /// <summary>
        /// 判断是否是数字
        /// </summary>
        /// <param name="input">要判断参数</param>
        /// <returns></returns>
        static bool IsNumeric(string input)
        {
            bool flag = true;
            string pattern=(@"^\d+$");
            Regex validate = new Regex(pattern);
            if(!validate.IsMatch(input))
            {
                flag = false;
            }
            return flag;
        }
        /// <summary>
        /// 进栈操作
        /// </summary>
        /// <param name="N">保存数字的棧</param>
        /// <param name="O">保存运算符的棧</param>
        /// <param name="exp">运算表达式</param>
        static void Calculate(Stack N,Stack O,string exp)
        {
            string ch, token = "";
            for (int i = 0; i < exp.Length;i++ )
            {
                ch = exp.Substring(i,1);
                if (IsNumeric(ch))
                {
                    token = ch;
                    N.Push(token);
                    token = "";
                }
                //if(ch==""||i==(exp.Length-1))
                //{
                //    N.Push(token);
                //    token = "";
                //}
                else if(ch=="+"||ch=="-"||ch=="*"||ch=="/")
                {
                    O.Push(ch);
                }
                if(N.Count==2)
                {
                    Compute(N,O);
                }
            }
 
        }
        /// <summary>
        /// 进行运算
        /// </summary>
        /// <param name="N">参与运算的数字的棧</param>
        /// <param name="O">参与运算的运算符的棧</param>
        static void Compute(Stack N,Stack O)
        {
            int oper1;
            int oper2;
            string oper;
            oper1 = Convert.ToInt32(N.Pop());
            oper2 = Convert.ToInt32(N.Pop());
            oper = Convert.ToString(O.Pop());
            switch(oper)
            {
                case"+":
                    N.Push(oper1+oper2);
                    break;
                case "-":
                    N.Push(oper1-oper2);
                    break;
                case "*":
                    N.Push(oper1*oper2);
                    break;
                case "/":
                    if (oper2 == 0)
                    {
                        throw new Exception("除数不能为0");
                    }
                    N.Push(oper1/oper2);
                    break;
            }
        }
    }
}

3、十进制向多种进制进行转换

static void Main(string[] args)
        {
            int num, baseNum;
            Console.Write("Enter a decimal number");
            num = Convert.ToInt32(Console.ReadLine());
            Console.Write("Enter a base");
            baseNum = Convert.ToInt32(Console.ReadLine());
            Console.WriteLine(num+"converts to");
            MulBase(num,baseNum);
            Console.WriteLine("Base"+baseNum);
            Console.ReadKey();
        }
        static void MulBase(int n,int b)
        {
            Stack digits = new Stack();
            do
            {
                digits.Push(n%b);
                n /= b;
            }while(n!=0);
            while(digits.Count>0)
            {
                Console.Write(digits.Pop());
            }
        }

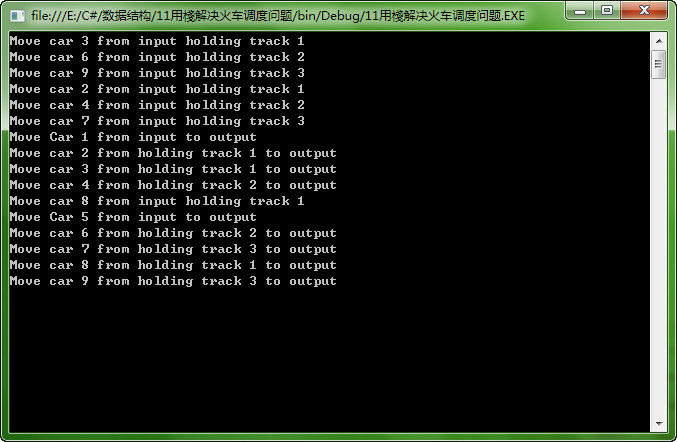
4、火车进站调度重组问题在C#中的实现

问题描述：假设一列货运列车共有n节编号分别为1~n的车厢，在进站前这n节车厢并不是按其编号有序排列；现要求重新排列各车厢，使该列车在

进入车站时，所有的车厢从前到后按编号1~n的次序排列。

interface IStack<T>
    {
        void Push(T item);//进栈操作
        T Pop();//出棧操作
        T Peek();//取数操作
        int GetLength();//求棧的长度
        bool IsEmpty();//判断棧是否为空
        void Clear();//清空棧操作
    }

 class SeqStack<T>:IStack<T>
    {
        //顺序栈的容量
        private int maxsize;
        //用于存储数序中的数据元素
        private T[] data;
        //指示顺序栈的栈顶
        private int top;
        //构建索引器
        public T this[int index]
        {
            get
            {
                return data[index];
            }
            set
            {
                data[index] = value;
            }
        }
        //棧容量属性
        public int Maxsize
        {
            get
            {
                return maxsize;
            }
            set
            {
                maxsize = value;
            }
        }
        //栈顶属性
        public int Top
        {
            get
            {
                return top;
            }
        }
        //初始化棧
        public SeqStack(int size)
        {
            data=new T[size];
            maxsize = size;
            top = -1;
        }
        //判断棧是否满
        public bool IsFull()
        {
            if (top == maxsize - 1)
            {
                return true;
            }
            else
            {
                return false;
            }
        }
        //判断棧是否为空
        public bool IsEmpty()
        {
            if (top == -1)
            {
                return true;
            }
            else
            {
                return false;
            }
        }
        //进栈操作
        public void Push(T item)
        {
            if (IsFull())
            {
                Console.WriteLine("Stack is full");
                return;
            }
            else
            {
                data[++top]=item;
            }
        }
        //出棧操作
        public T Pop()
        {
            T temp=default(T);
            if (IsEmpty())
            {
                Console.WriteLine("Stack is empty");
                return temp;
            }
            else
            {
                temp = data[top];
                --top;
                return temp;
            }
        }
        //获取栈顶元素
        public T Peek()
        {
            if(IsEmpty())
            {
                Console.WriteLine("Stack is empty");
                return default(T);
            }
            else
            {
                return data[top];
            }
        }
        //获取棧的长度
        public int GetLength()
        {
            return top + 1;
        }
        //清空棧
        public void Clear()
        {
            top = -1;
        }
    }

class TrainAyyayrangeByStack
    {
        //车厢重排算法，K个缓冲铁轨，车厢初始排序存放在p中
        public bool Railroad(int[] p, int n, int k)
        {
            //重排成功返回true，否则返回false
            //创建与缓冲铁轨对应的堆栈
            SeqStack<int>[] H = new SeqStack<int>[k+1];
            for (int i = 1; i <= k;i++ )
            {
                H[i] = new SeqStack<int>(p.Length);
            }
            //初始化第一个出棧车厢号1
            int NowOut = 1;
            //初始设置缓冲铁轨中编号最小的车厢
            int minH = n+1;
            //初始minH号车厢对应的缓冲铁轨号
            int minS = 0;
            //车厢重排
            for (int i = 0; i < n;i++ )
            {
                //如果即将入站的车厢号和下一个即将出站的车厢号一致，就直接输出
                if (p[i] == NowOut)
                {
                    Console.WriteLine("Move Car {0} from input to output", p[i]);
                    //输出后将下一个即将出站的车厢号重置
                    NowOut++;
                    //从缓冲铁轨中输出
                    while (minH == NowOut)
                    {
                        Output(ref minH, ref minS, ref H, k, n);
                        NowOut++;
                    }
                }
                //如果即将入站的车厢号和下一个即将出战的车厢号不一致，就将其保存在缓冲铁轨中
                else
                {
                    //将p[i]送入某个缓冲铁轨
                    if(!Hold(p[i],ref minH,ref minS,ref H,k,n))
                    {
                        return false;
                    }
                }
            } return true;
        }
        //把车厢从缓冲铁轨送至出轨处，同时修改minS和minH
        void Output(ref int minH,ref int minS,ref SeqStack<int>[]H,int k,int n)
        {
            //车厢索引
            int c;
            //从堆栈minS中删除编号最小的车厢minH
            c = H[minS].Pop();
            Console.WriteLine("Move car {0} from holding track {1} to output",c,minS);
            //通过检查所有的栈顶，搜索新的minH和minS
            minH = n + 2;
            for (int i = 1; i <= k;i++ )
            {
                if(!H[i].IsEmpty()&&(H[i].Peek())<minH)
                {
                    minH = H[i].Peek();
                    minS = i;
                }
            }
        }
        //在一个缓冲铁轨中放入车厢c
        bool Hold(int c,ref int minH,ref int minS,ref SeqStack<int>[]H,int k,int n)
        {
            //如果没有可用的缓冲铁轨，则返回false
            //否则返回true
            //为车厢c寻找最优的缓冲铁轨
            //初始化最优铁轨和最优栈顶车厢号
            int BestTrack = 0;
            int BestTop = n + 1;
            //车厢索引
            int x;
            //扫描缓冲铁轨，寻找最优的缓冲铁轨棧，即栈顶元素相对最小
            for (int i = 1; i <= k;i++ )
            {
                //如果缓冲铁轨不为空
                if (!H[i].IsEmpty())
                {
                    x = H[i].Peek();
                    if (c < x && x < BestTop)
                    {
                        //铁轨i顶部的车厢编号最小
                        BestTop = x;
                        BestTrack = i;
                    }
                }
                //铁轨i为空
                else
                {
                    if(BestTrack==0)
                    {
                        BestTrack = i;
                    }
                    break;
                }
            }
            //没有可用铁轨
            if(BestTrack==0)
            {
                return false;
            }
            //把车厢c送入缓冲铁轨
            H[BestTrack].Push(c);
            Console.WriteLine("Move car {0} from input to holding track {1}",c,BestTrack);
            //如果条件成立就修改缓冲铁轨中下一个将要出站的车厢号
            if (c < minH)
            {
                minH = c;
                minS = BestTrack;
            }
            return true;
        }

static void Main(string[] args)
        {
            int[] p = new int[] { 3,6,9,2,4,7,1,8,5};
            int k = 3;
            TrainAyyayrangeByStack ta = new TrainAyyayrangeByStack();
            bool result;
            result = ta.Railroad(p,p.Length,k);
 
            do
            {
                if(result==false)
                {
                    Console.WriteLine("need more holding track,please enter additional");
                    k = k + Convert.ToInt32(Console.ReadLine());
                    result = ta.Railroad(p,p.Length,k);
                }
            }while(result==false);
            Console.ReadKey();
        }