canvas绘制贝塞尔曲线
1、绘制二次方贝塞尔曲线
quadraticCurveTo(cp1x,cp1y,x,y); 其中参数cp1x和cp1y是控制点的坐标,x和y是终点坐标
数学公式表示如下:
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
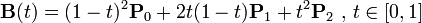

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title></title>
<style type="text/css">
*{padding: 0;margin:0;}
body{background: #1b1b1b;}
#div1{margin:50px auto; width:300px; height: 300px;}
canvas{background: #fff;}
</style>
<script type="text/javascript">
window.onload = function(){
var c = document.getElementById('myCanvas');
var content = c.getContext('2d'); //绘制二次方贝塞尔曲线
content.strokeStyle ="#FF5D43";
content.beginPath();
content.moveTo(0,200);
content.quadraticCurveTo(75,50,300,200);
content.stroke();
content.globalCompositeOperation = 'source-over'; //目标图像上显示源图像 //绘制上面曲线的控制点和控制线,控制点坐标为两直线的交点(75,50)
content.strokeStyle = '#f0f';
content.beginPath();
content.moveTo(75,50);
content.lineTo(0,200);
content.moveTo(75,50);
content.lineTo(300,200);
content.stroke(); };
</script>
</head>
<body>
<div id="div1">
<canvas id="myCanvas" width="300" height="200"></canvas>
</div>
</body>
</html>

2、三次方贝塞尔曲线
bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y) 其中参数cp1x,cp1y表示第一个控制点的坐标, cp2x,cp2y表示第二个控制点的坐标, x,y是终点的坐标;
数学公式表示如下:
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
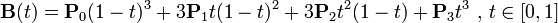

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title></title>
<style type="text/css">
*{padding: 0;margin:0;}
body{background: #1b1b1b;}
#div1{margin:50px auto; width:300px; height: 300px;}
canvas{background: #fff;}
</style>
<script type="text/javascript">
window.onload = function(){
var c = document.getElementById('myCanvas');
var content = c.getContext('2d'); //三次方贝塞尔曲线
content.strokeStyle = '#FA7E2A';
content.beginPath();
content.moveTo(25,175);
content.bezierCurveTo(60,80,150,30,170,150);
content.stroke();
content.globalCompositeOperation = 'source-over'; //绘制起点、控制点、终点
content.strokeStyle = 'red';
content.beginPath();
content.moveTo(25,175);
content.lineTo(60,80);
content.lineTo(150,30);
content.lineTo(170,150);
content.stroke(); };
</script>
</head>
<body>
<div id="div1">
<canvas id="myCanvas" width="300" height="200"></canvas>
</div>
</body>
</html>

canvas绘制贝塞尔曲线的更多相关文章
- 用html5的canvas画布绘制贝塞尔曲线
查看效果:http://keleyi.com/keleyi/phtml/html5/7.htm 完整代码: <!DOCTYPE html PUBLIC "-//W3C//DTD XHT ...
- JavaScript+canvas 利用贝塞尔曲线绘制曲线
效果图: <body> <canvas id="test" width="800" height="300">< ...
- Canvas中绘制贝塞尔曲线
① 什么是贝塞尔曲线? 在数学的数值分析领域中,贝济埃曲线(英语:Bézier curve,亦作“贝塞尔”)是计算机图形学中相当重要的参数曲线.更高维度的广泛化贝济埃曲线就称作贝济埃曲面,其中贝济埃三 ...
- HTML5 canvas绘制线条曲线
HTML5 canvas入门 线条例子 1.简单线条 2.三角形 3.填充三角形背景颜色 4.线条颜色以及线条大小 5.二次贝塞尔曲线 6.三次贝塞尔曲线 <!doctype html> ...
- Unity GUI内绘制贝塞尔曲线
用Handles可以直接在GUI下绘制贝塞尔 using UnityEditor; using UnityEngine; using System.Collections; public class ...
- Android 贝塞尔曲线解析
相信很多同学都知道"贝塞尔曲线"这个词,我们在很多地方都能经常看到.利用"贝塞尔曲线"可以做出很多好看的UI效果,本篇博客就让我们一起学习"贝塞尔曲线 ...
- Canvas学习:封装Canvas绘制基本图形API
Canvas学习:封装Canvas绘制基本图形API Canvas Canvas学习 从前面的文章中我们了解到,通过Canvas中的CanvasRenderingContext2D对象中的属性和方 ...
- canvas贝塞尔曲线
贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线. 曲线定义:起始点.终止点.控制点.通过调整控制点,贝塞尔曲线的形状会发生变化. 1962年,法国数学家Pierr ...
- [js高手之路] html5 canvas系列教程 - arcTo(弧度与二次,三次贝塞尔曲线以及在线工具)
之前,我写了一个arc函数的用法:[js高手之路] html5 canvas系列教程 - arc绘制曲线图形(曲线,弧线,圆形). arcTo: cxt.arcTo( cx, cy, x2, y2, ...
随机推荐
- 非常棒的Visual Studo调试插件:OzCode 2.0 下载地址
最新版下载地址 http://download.csdn.net/detail/simadi/8925511 如果你是一名C#开发者,那么,你则需要OzCode.它将可视化调试的概念上升到了一个新的高 ...
- Linux lspci查看硬件设备
Linux 主机的硬件配备 lspci 找到的是眼下主机上面的硬件配备 [root@www ~]# lspci [-vvn] 选项与參数: -v :显示很多其它的 PCI 接口装置的具体信息 ...
- crm操作观点
using System; using Microsoft.Xrm.Sdk; using Microsoft.Crm.Sdk.Messages; /// <summary> ...
- 认识input输入框的placeholder属性
我们来认识下input输入框的placeholder属性. placeholder 属性提供可描述输入字段预期值的提示信息.(placeholder 属性适用于以下的 <input> 类型 ...
- ORACLE 实验一
实验一:数据定义 实验学时:4学时 实验类型:综合型 实验要求:必修 一.实验目的 1.熟悉Oracle的client配置: 2.掌握SQL Plus的使用: 3.掌握SQL模式定义语句,定义相关的表 ...
- C++该函数隐藏
只有基类成员函数的定义已声明virtualkeyword,当在派生类中的时间,以支付功能实现,virtualkeyword可以从时间被添加以增加.它不影响多状态. easy混淆视听,掩盖: ,规则例如 ...
- 于windows建筑物Cocos2d-x win32开发环境
这份文件是从cocos2d-x复制的官网.. . 在windows7上搭建COCOS2D-X开发环境并不难. 可是因为框架更新过快,非常多用户都有困难.我希望你们觉得这个教程实用. 建议:为了避 ...
- error C2871: 'std' : does not exist or is not a namespace
#include <iostream.h> using namespace std; 然后编译时出现 error C2871: 'std' : does not exist or is n ...
- 几个cd快速提示
cd是project师每天都会用到的命令. 今天就来分享几条和cd有关的小技巧 cd 假设你用cd ~来进入当前用户的home文件夹的话,那么能够试试直接敲cd. 相同效果,少敲两下键盘. cd - ...
- hdu 1290 竭诚为杭州电礼物50周年
专门为杭州电50周年礼事 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Tot ...
