【BZOJ3894】【Luogu3358】文理分科 - 最小割多选一模型

链接Click Here

这个题就是个板子的最小割多选一模型啦\(QwQ\)，这里介绍一种通用的解法。

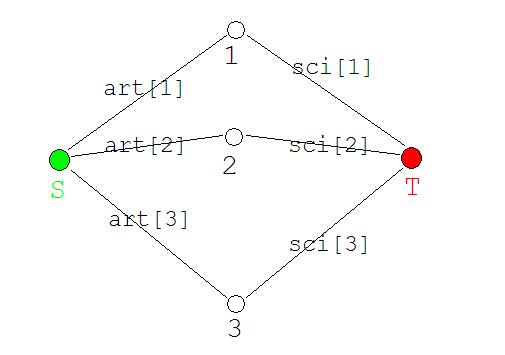
抛开组合收益不谈，这个题就是一个简单的最小割模型。我们只需要建出来这样一张图，在上面跑最小割，割掉的就是不用的，留下来的就是最大收益啦_(≧▽≦)/，是不是很显然呢？

如果要考虑组合收益的话，我们把这个组合收益实体化成一个点来进行处理。还是上面那个图，我们假设\(2\), \(3\)是以和\(1\)四连通的两个点。这样的话我们需要保证一件事情：

• 在\(art_1, art_2, art_3\)中，只要有一个被割掉（不选），那么\(art\)的组合收益就同时被割掉。

• 在\(sci_1, sci_2, sci_3\)中，只要有一个被割掉（不选），那么\(sci\)的组合收益就同时被割掉。

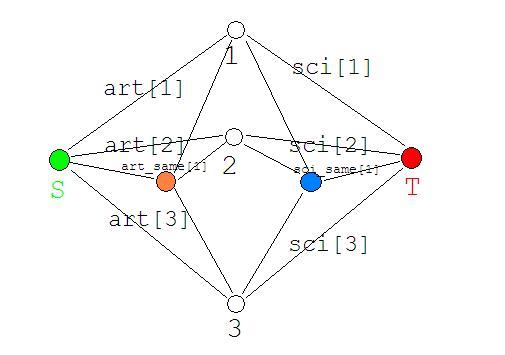
根据这些要求，我们建出来了下面这样的一张图。

很显然，这张图是可以满足上面的性质的。我们这样连边来看一下。

• \(s -> art\_same(i, j)\) \(flow = art\_ex[i][j]\)

• \(art\_same(i, j) -> linked\_nodes\) \(flow = INFF\)

思考一下，假如我们割掉了\(art\)中的任意一个，那么\(sci\)那边一定有对应的边没有割掉，这样我们的\(art\_same[1]\)就会顺着没有被割掉的边流走啦\(QwQ\)(也就是还是被割掉了\(QwQ\))

同理，理科那边和更多点的情况，这种图都是适用的。

关键需要注意的一件事情：在建图的时候，因为可能会出现\(art\_same[i]\)太大而另外一边的流量太小，无法完全割断的情况，我们要给它加上一个\(INF\)，在最后求和的时候再减掉。而且这个\(INF\)一定要低于\(INFF\)的数量级，中间的边一定要保证是不能割掉的！这一点相当重要。

这种图是一种非常重要的最小割模型图，一定要会啊\(QwQ\)

#include <bits/stdc++.h>
#define N 30100
#define M 480010
#define int long long
using namespace std;

const int INF = 0x3f3f3f3f;
const int INFF = 0x3f3f3f3f3f3f3f3fll;

int n, m, art[105][105], sci[105][105];
int art_ex[105][105], sci_ex[105][105];

int node (int x, int y) {return (x - 1) * m + y;}
int same_art (int x, int y) {return n * m * 1 + node (x, y);}
int same_sci (int x, int y) {return n * m * 2 + node (x, y);}

int mv[5][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

bool in_map (int x, int y) {
	return 1 <= x && x <= n && 1 <= y && y <= m;
}

int cnt = -1, head[N];

struct edge {
	int nxt, to, f;
}e[M];

void add_edge (int from, int to, int flw) {
	e[++cnt].nxt = head[from];
	e[cnt].to = to;
	e[cnt].f = flw;
	head[from] = cnt;
}

queue <int> q;
#define fpop(x) x.front();x.pop()

int cur[N], deep[N];

bool bfs (int s, int t) {
	memcpy (cur, head, sizeof (head));
	memset (deep, 0x3f, sizeof (deep));
	deep[s] = 1; q.push (s);
	while (!q.empty ()) {
		int u = fpop (q);
		for (int i = head[u]; ~i; i = e[i].nxt) {
			int v = e[i].to;
			if (e[i].f && deep[v] == INFF) {
				deep[v] = deep[u] + 1;
				q.push (v);
			}
		}
	}
	return deep[t] != INFF;
}

int dfs (int u, int t, int lim) {
	if (u == t || !lim) {
		return lim;
	}
	int tmp = 0, flow = 0;
	for (int &i = cur[u]; ~i; i = e[i].nxt) {
		int v = e[i].to;
		if (deep[v] == deep[u] + 1) {
			tmp = dfs (v, t, min (lim, e[i].f));
			lim -= tmp;
			flow += tmp;
			e[i ^ 0].f -= tmp;
			e[i ^ 1].f += tmp;
			if (!lim) break;
		}
	}
	return flow;
}

int Dinic (int s, int t) {
	int min_cut = 0;
	while (bfs (s, t)) {
		min_cut += dfs (s, t, INFF);
	}
	return min_cut;
}

signed main () {
	memset (head, -1, sizeof (head));
	cin >> n >> m;
	int s = n * m * 3 + 1, t = n * m * 3 + 2;
	for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> art[i][j];
	for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> sci[i][j];
	for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> art_ex[i][j];
	for (int i = 1; i <= n; ++i) for (int j = 1; j <= m; ++j) cin >> sci_ex[i][j];

	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			add_edge (s, node (i, j), art[i][j]); add_edge (node (i, j), s, 0);
			add_edge (node (i, j), t, sci[i][j]); add_edge (t, node (i, j), 0);
		}
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			add_edge (s, same_art (i, j), art_ex[i][j]); add_edge (same_art (i, j), s, 0);
			add_edge (same_sci (i, j), t, sci_ex[i][j]); add_edge (t, same_sci (i, j), 0);
			for (int k = 0; k < 5; ++k) {
				int tx = i + mv[k][0], ty = j + mv[k][1];
				if (in_map (tx, ty)) {
					add_edge (same_art (i, j), node (tx, ty), INFF); add_edge (node (tx, ty), same_art (i, j), 0);
					add_edge (node (tx, ty), same_sci (i, j), INFF); add_edge (same_sci (i, j), node (tx, ty), 0);
				}
			}
		}
	}
	int ans = 0;// n * m * INF;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			ans += art[i][j] + sci[i][j] + art_ex[i][j] + sci_ex[i][j];
		}
	}
	cout << ans - Dinic (s, t) << endl;
}