logistics回归简单应用（二）

警告：本文为小白入门学习笔记

网上下载的数据集链接:https://pan.baidu.com/s/1NwSXJOCzgihPFZfw3NfnfA 密码: jmwz

不知道这个数据集干什么用的，根据直观分析应该属于分类问题，有两个变量X1和X2，Y取值非零即一，用MATLAB分析发现第二列对Y的影响较为明显

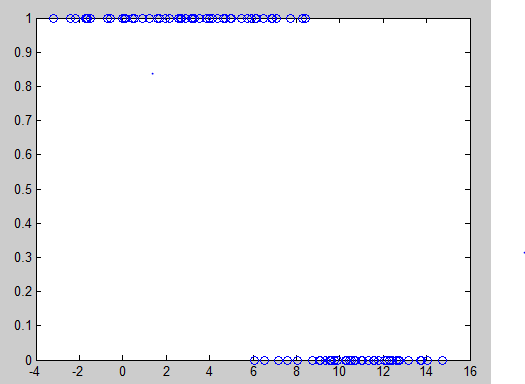
大致以8为分界线，8右边Y值为0,8左边Y为1.

首先假设舍去属性X1，设数据集为（X2，Y）。然后分别用线性回归（Liner regression）和逻辑回归（logistics regression）对数据集进行分类分析比较。最后再把属性X1加上看看结果怎么样。

（1）假设函数（hypothesis function）：

　　参数（parameter）设为w = [w1；w2];

　　hw（x） = w1 + w2x;

（2）代价函数（cost function）：

　　J（w） = 1/2m∑（hw(x(i)) - y(i)）^2 ;  （m是数据集的个数，乘上2是为了后来求导时候方便）

　　J（w） = 1/200∑（w1 + w2x(i) - y(i)）^2;

（3）梯度下降算法（gradient descent algorithm）求解出参数w1和w2：

　　w1 ：= ðJ（w1，w2）/ðw1 = 1/m∑（hw(x(i)) - y(i)）;

　　w2 ：= ðJ（w1，w2）/ðw2 = 1/m∑（hw(x(i)) - y(i)）x(i);

　　（ð表示求偏导）

　　repeat until convergence {

　　　　w1 ：= w1 - α1/m∑（hw(x(i)) - y(i)）;

　　　　w2 ：= w2 - α1/m∑（hw(x(i)) - y(i)）x(i);

　　};

　　(α是步长，使用MATLAB/octave是自动选取)

　　注意：在每次更新w1，w2时候应该注意更新的顺序，应该是先一起计算再一同更新，也就是每一次更新时，w1和w2的值都在变化。

　　接下来就使用MATLAB（octave也可以）来测试整个分析过程是否正确，然后再用python代码实现。

（4）MATLAB模拟（octave同理可用）

新建一个costFunction.m文件 写入函数：

function[jval,gradient] = costFunction(w)
filename = 'testSet.txt';
A = importdata(filename);
x = A(:,2);
y = A(:,3);

m = 0;
for i = 1:100
　　m = m + (w(1) + w(2) * x(i) - y(i)).^2;
end
jval = 1/200 * m;

n = 0;
for i = 1:100
　　n = n + (w(1) + w(2) * x(i) - y(i));
end
gradient(1) = 1/100 * n;

n = 0;
for i = 1:100
　　n = n + (w(1) + w(2) * x(i) - y(i))*x(i);
end
gradient(2) = 1/100 * n;

　　命令行窗口输入：

>> options = optimset('GradObj','on','MaxIter',100);
>> initialW = zeros(2,1);
>> [optW,functionVal,exitFlag] = fminunc(@costFunction,initialW,options)

　　返回结果：

optW =

1.1202
-0.0897

functionVal =

0.0385

exitFlag =

1

　　结果表明：

　　w1 = 1.1202   ;   w2 = -0.0897  ;  函数返回的结果是0.0385（这个值越接近零，表示拟合的越好）  ；extiFlag = 1表示收敛

（5）画出图像

既然已经得到了w1和w2的值那就可以画出假设函数（hypothesis function）看看这么样吧！！

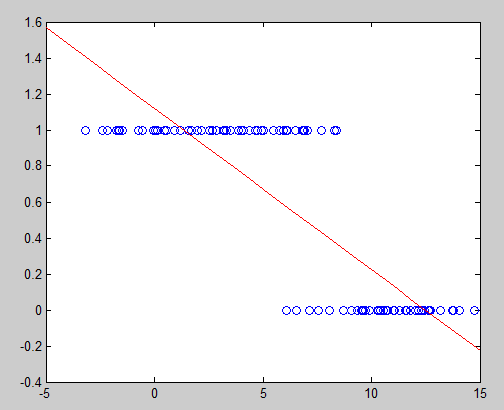
结果是这样的，这是线性回归结果，但是对于分类为题，这样做并不是什么好主意（只是用它来作比较练练手），所以接下来选用logistics回归试一试。

因为对于这个数据集，函数值Y = 0 or 1，所以希望对于输入值x，假设函数 0<=Y<=1，这样最好不过了！

不同之处需要改变假设函数（hypothesis function）：

hw(x) = g(w'x)      (这里'为转置的意思)

g(z) = 1/(1+e‾^z)

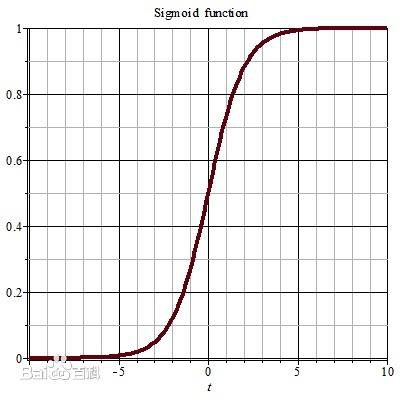
那么这个时候hw（x）表示的什么意识呢？函数的输出值是对输入值x可能性的评价

例如：判断一个肿瘤（tumor）是良性还是恶性，  假如现在只取肿瘤大小x这个属性进行分析。

如果当x为一定值时 hw(x) = 0.7，可以说这个肿瘤有70%的概率是恶性肿瘤。

所以：hw(x) = P(y=1|x;w)        (表示在x，w的条件下，y=1的概率是多少)

（1）首先让表达式以矩阵的形式表示

　　w = [w1;w2]  ;  x = [1;x];

　　z = w1 + w2x = w'x;

　　hw(z) =   1/(1+e‾^z);

然后如何计算w1和w2呢？

（2）代价函数（cost function）

　　J（w） = 1/m∑1/2（hw(x(i)) - y(i)）^2 ;

　　设：cost（hw(x),y） = 1/2（hw(x) - y）^2;

　　 cost（hw(x),y）= -log（hw(x)） if y=1;

　　 cost（hw(x),y）= -log（1 - hw(x)） if y=0;

　　合并成一个连续函数：

　　 cost（hw(x),y）= -y*log(hw(x)) - (1-y)*log(1-hw(x));

　　代入代价函数中得：

　　J(w) = -1/m[∑-y(i)*log(hw(x(i))) - (1-y(i)*log(1-hw(x(i)))];

（3）梯度下降算法（gradient descent algorithm）

　　repeat{

　　wj :=wj - α(δJ(w)/δwj), (j = 1,2......n)

}

(α学习步长)

求偏导（懒得打字了）：

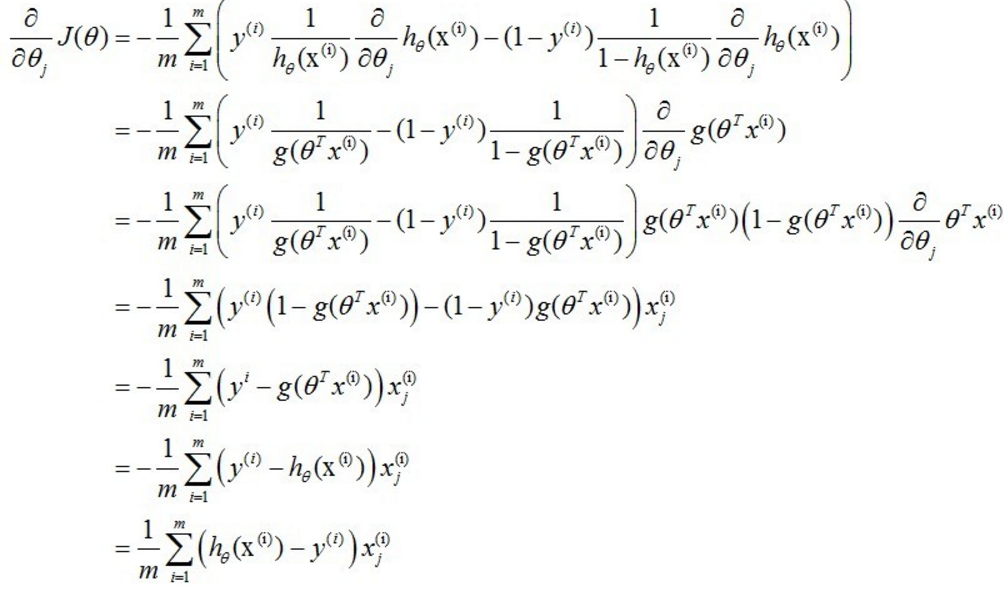
更新过程就可以写成

repeat{

　　wj ：= wj - α1/m∑（hw(x(i)) - y(i)）xj(i) ；     (j = 1,2......n)

}

其中x0 = 1； 是不是十分眼熟，这个式子和上面的式子一样，只是假设函数hw（x）不同罢了。

（4）MATLAB实现

　　

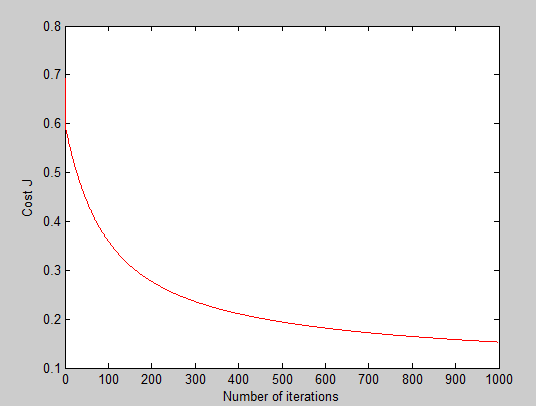
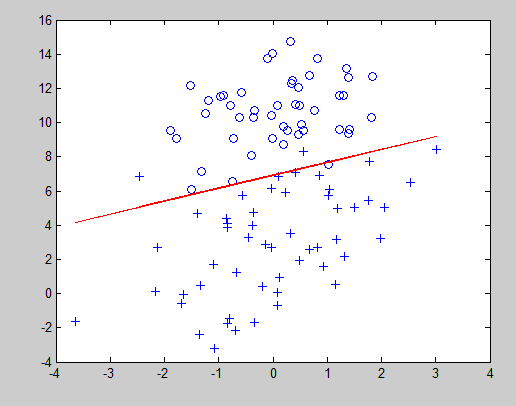
决策曲线：