BZOJ5093图的价值(斯特林数)

题目描述

“简单无向图”是指无重边、无自环的无向图（不一定连通）。

一个带标号的图的价值定义为每个点度数的k次方的和。

给定n和k，请计算所有n个点的带标号的简单无向图的价值之和。

因为答案很大，请对998244353取模输出。

题解

因为懒得敲公式了，所以就直接粘题解了。

我们发现在这张图中每个点都是等价的，所以我们就只需要考虑一个点的贡献，最后乘上n就可以了。

、

当一个点的度数为i时，我们可以从其他n-1个点中任意挑出i个点和它连边，而其余n-1个点之间可以任意连边。

然后我们发现后面那一坨和i无关，可以放到前面去，所以我们实际上是在求

然后i^k这种东西有一个恒等式

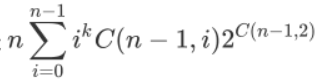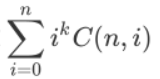
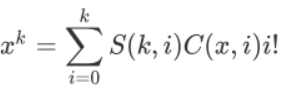
S(k,i)为第二类斯特林数，意义为k个小球放入i个不同的盒子里的方案数。

等式的左边意义为把k个不同小球放到x个不同的盒子中的方案数。

右边是在枚举有哪些盒子里有球，还是比较好理解的。

那么我们把这个指数的东西代换完后式子变成了

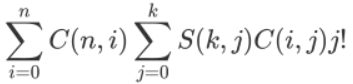
把枚举j的sigma提前

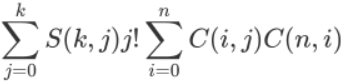
后面的那个东西看起开很难受，如果我们可以把n和j放在一起，式子就可以往前放了。

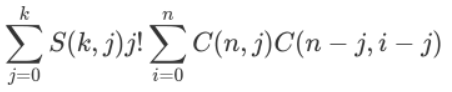
从n个小球中选i个，再从i个中选j个等价于从n个小球中选j个，再从剩下的(n-j)个中选(i-j)个。

于是我们就可以吧C(n,j)提前了，后面的组合数可以直接用恒等式换掉。

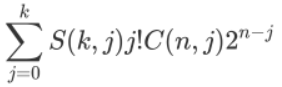
然后我们只要求出所有S(k,j)就可以了，这个用NTT解决。

代码

#include<iostream>
#include<cstdio>
#define N 2000009
using namespace std;
typedef long long ll;
const int G=;
const int Gi=;
const int mod=;
ll l,L,a[N],b[N],jie[N],ni[N],nii[N],n,k,ans,c[N];
int rev[N];
ll power(ll x,ll y){
    if(y<)return ;
    ll ans=;x%=mod;
    while(y){if(y&)ans=ans*x%mod;x=x*x%mod;y>>=;}
    ans=(ans+mod)%mod;
    return ans;
}
inline ll ny(ll x){return power(x,mod-);}
inline ll C(ll n,ll m){return jie[n]*ni[m]%mod*ni[n-m]%mod;}
inline void NTT(ll *a,int tag){
    for(int i=;i<l;++i)if(i>rev[i])swap(a[i],a[rev[i]]);
    for(int i=;i<l;i<<=){
        ll wn=power(tag==?G:Gi,(mod-)/(i<<));
        for(int j=;j<l;j+=(i<<)){
          ll w=;
          for(int k=;k<i;++k,w=w*wn%mod){
               ll x=a[j+k],y=a[i+j+k]*w%mod;
               a[j+k]=(x+y)%mod;a[i+j+k]=(x-y+mod)%mod;
          }
        }
   }
}
int main(){
//    cout<<power(3,mod-2);
    scanf("%lld%lld",&n,&k);
    ll yu=n%mod*power(,(n-)*(n-)/)%mod;n--;
    jie[]=;
    for(int i=;i<=k;++i)jie[i]=jie[i-]*i%mod;ni[k]=power(jie[k],mod-);
    for(int i=k-;i>=;--i)ni[i]=ni[i+]*(i+)%mod;
    for(int i=;i<=k;++i)a[i]=(power(-,i)*ni[i]+mod)%mod;
    for(int i=;i<=k;++i)b[i]=power(i,k)*ni[i]%mod;
    l=;L=;
    while(l<=(k<<))l<<=,L++;
    for(int i=;i<l;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
    NTT(a,);NTT(b,);
    for(int i=;i<l;++i)a[i]=a[i]*b[i]%mod;
    NTT(a,-);ll nn=ny(l);
    c[]=;
    for(int i=;i<=min(k,n);++i)c[i]=c[i-]*ny(i)%mod*(n-i+)%mod;
    for(int i=;i<=k;++i){
      a[i]=a[i]*nn%mod;
      (ans+=a[i]*jie[i]%mod*c[i]%mod*power(,n-i)%mod)%=mod;
    }
    ans=ans*yu%mod;
    cout<<ans;
    return ;
}