BZOJ3172 后缀数组

题意：求出一篇文章中每个单词的出现次数

对样例的解释：

原文是这样的：

a
aa
aaa

注意每个单词后都会换行

所以a出现次数为6，aa为3 (aa中一次，aaa中两次)，aaa为1

标准解法好像是AC自动机or后缀自动机，还有人用KMP暴力过的= =

用后缀数组做的。原来没刷过这种类型，顺便复习一下~

Reference：http://blog.sina.com.cn/s/blog_6e63f59e0101bpw5.html

以样例为例：

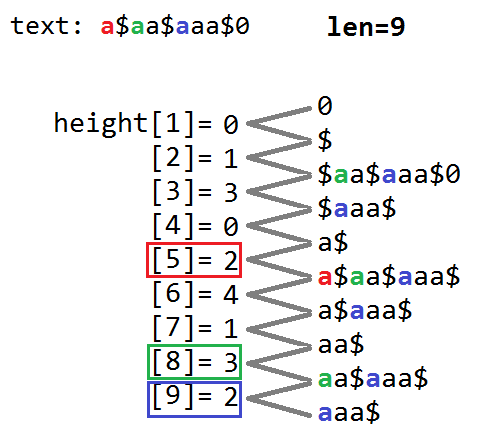
对于每个单词第一个字母对应的height，向上、向下数出height值大于等于单词长度的height的个数。

注意细节的处理= =

 //在BT5下attack的时候把数值调大点(超过2000）就行了，具体可以参见网上破解无线网密码的文章，就是抓包之后的那步，注入数据包的命令
 #include "iostream"
 #include "cstring"
 using namespace std;
 #define maxn 1010000

 int wa[maxn],wb[maxn],wv[maxn],wws[maxn];
 int rank[maxn],height[maxn];
 int r[maxn],sa[maxn],ans[maxn],st[maxn],ln[maxn];
 int n,len,tl;
 char ts[maxn];

 int cmp(int *r,int a,int b,int l)
 {
     return r[a]==r[b]&&r[a+l]==r[b+l];
 }

 void da(int *r,int *sa,int n,int m)
 {
     int i,j,p,*x=wa,*y=wb,*t;
     for(i=; i<m; i++) wws[i]=;
     for(i=; i<n; i++) wws[x[i]=r[i]]++;
     for(i=; i<m; i++) wws[i]+=wws[i-];
     for(i=n-; i>=; i--) sa[--wws[x[i]]]=i;
     for(j=,p=; p<n; j*=,m=p)
     {

         for(p=,i=n-j; i<n; i++) y[p++]=i;
         for(i=; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
         for(i=; i<n; i++) wv[i]=x[y[i]];
         for(i=; i<m; i++) wws[i]=;
         for(i=; i<n; i++) wws[wv[i]]++;
         for(i=; i<m; i++) wws[i]+=wws[i-];
         for(i=n-; i>=; i--) sa[--wws[wv[i]]]=y[i];
         for(t=x,x=y,y=t,p=,x[sa[]]=,i=; i<n; i++)
             x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;
     }
     return;
 }

 void calheight(int *r,int *sa,int n)
 {
     int i,j,k=;
     for(i=; i<=n; i++) rank[sa[i]]=i;
     for(i=; i<n; height[rank[i++]]=k)
         for(k?k--:,j=sa[rank[i]-]; r[i+k]==r[j+k]; k++);
     return;
 }

 int main()
 {
     ios::sync_with_stdio(false);
     cin>>n;
     len=;
     for (int i=;i<=n;i++)
     {
         st[i]=len;
         cin>>ts;
         tl=strlen(ts);
         ln[i]=tl;
         for (int j=len;j<len+tl;j++)
         {
             char ch=ts[j-len];
             int tn=ch;
             r[j]=tn;
         }
         len+=tl;
         r[len]=;
         len++;
     }
     r[len]=;

     da(r,sa,len+,);
     calheight(r,sa,len);

     //for (int i=0;i<=len+1;i++)
     //    cout<<height[i]<<" ";
     //cout<<endl;
     for (int i=;i<=n;i++)
     {
         int tmp=rank[st[i]];
         int tl=tmp,tr=tmp+,tlen=ln[i];
         while ((height[tl]>=tlen)&&(tl>=))      tl--;
         while ((height[tr]>=tlen)&&(tr<=len))   tr++;
         cout<<tr-tl<<endl;
     }

     return ;
 }