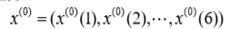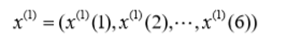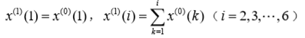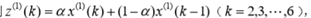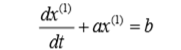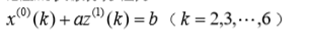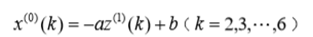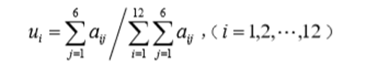【数学建模】day14-建立GM(1,1)预测评估模型应用

学习建立GM(1,1)灰色预测评估模型，解决实际问题：

SARS疫情对某些经济指标的影响问题

一、问题的提出

　　2003 年的 SARS 疫情对中国部分行业的经济发展产生了一定影响，特别是对部分 疫情较严重的省市的相关行业所造成的影响是显著的，经济影响主要分为直接经济影响 和间接影响。直接经济影响涉及商品零售业、旅游业、综合服务等行业。很多方面难以 进行定量的评估，现仅就 SARS 疫情较重的某市商品零售业、旅游业和综合服务业的影 响进行定量的评估分析。

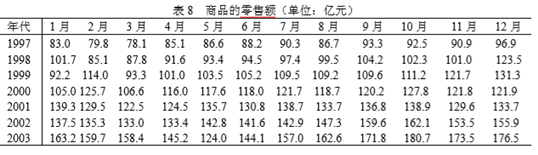
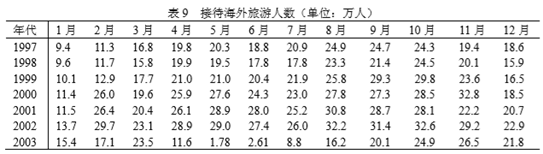
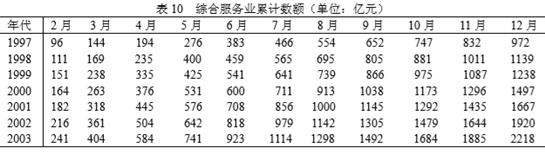
　　究竟 SARS 疫情对商品零售业、旅游业和综合服务业的影响有多大，已知某市从 1997 年 1 月到 2003 年 12 月的商品零售额、接待旅游人数和综合服务收入的统计数据如下面三表所示。

　　

　　

　　

　　试根据这些历史数据建立预测评估模型，评估 2003 年 SARS 疫情给该市的商品零 售业、旅游业和综合服务业所造成的影响。

二、模型的分析与假设

模型分析：

　　根据所掌握的历史统计数据可以看出，在正常情况下，全年的平均值较好地反映了相关指标的变化规律。这样，对于每一个经济指标，考虑从两部分着手建立预测评估模型：

1. 利用灰色理论建立GM(1,1)模型，根据1997-2002年的平均值序列，预测2003年的平均值。
2. 通过历史数据计算每一个月的指标值与全年总值之间的关系，并将此关系拓展到2003年，进而预测出2003年每一个月的指标值。进而与真实数据值作比较，从而得出结论。

模型假设：

1. 假设所有的统计数据真实可靠。
2. 假设该市SARS疫情流行期间和结束之后，数据的变化只与SARS疫情的影响有关，不考虑其他随机因素的影响。

三、建立灰色预测模型GM(1,1)

　　由已知数据，对于1997-2002年的某项指标记为A= (a_ij)_6*12,计算每年的平均值作为初始数列。记为：

　　　　　　

　　并要求级比。对x(0)做一次累加得1-AGO序列：

　　　　　　

　　式中：

　　　　　　

　　取x(1)的加权均值序列：

　　　　　　

　　式中，α是确定参数。

　　从而，GM(1,1)的白化微分方程模型为：

　　　　　　

　　其中a是发展灰度，b 是内生控制灰度。

　　相应的灰微分方程为：

　　　　　　

　　或记为：

　　　　

　　

　　这样，我们就得到了微分方程的解。

　　根据解式，我们可以求出2003年的平均值x拔，从而得到2003年的全年总值Z。

　　另一方面，根据历史数据，得到第i个月指标值占全年总值的比重为：

　　　　　　

　　此比重拓展到2003年，可以得到2003 年每一个月的指标值V =zu 。

四、模型的求解

　　对三项指标建立的微分方程模型分别求解如下：

　　（1）商品零售额

　　第一指标的数据保存han1.txt，数据如下：

83.0   79.8   78.1   85.1   86.6   88.2   90.3   86.7    93.3    92.5    90.9    96.9
101.7  85.1   87.8   91.6   93.4   94.5   97.4   99.5   104.2   102.3   101.0    123.5
92.2  114.0   93.3  101.0  103.5  105.2  109.5  109.2   109.6   111.2   121.7    131.3
105.0 125.7  106.6   116.0  117.6  118.0  121.7  118.7   120.2   127.8   121.8   121.9
139.3 129.5  122.5   124.5  135.7  130.8  138.7  133.7   136.8   138.9   129.6   133.7
137.5 135.3  133.0   133.4  142.8  141.6  142.9  147.3   159.6   162.1   153.5   155.9
163.2 159.7  158.4   145.2  124.0  144.1  157.0  162.6   171.8   180.7   173.5   176.5 

　计算的matlab程序如下：

 1 clc,clear
 2  load han1.txt
 3  han1(end,:) = []; %删除最后一行，即2003年的值
 4 m  = size(han1,2); %矩阵列数
 5 x0 = mean(han1,2); %矩阵每一行均值
 6 x1 = cumsum(x0); %1-AGO序列
 7 alpha = 0.4;
 8  n = length(x0);
 9  z1 = alpha*x1(2:n) +(1-alpha) * x1(1:n-1); %邻值生成值
10 Y = x0(2:n);
11  B = [-z1,ones(n-1,1)];
12  ab = B\Y %最小二乘拟合参数
13 %下面求年平均值的预测值，取n=6预测下一年度
14 x_hat = (x0(1) - ab(2)/ab(1)) *(exp(-ab(1)*n)-exp(-ab(1)*(n-1)))
15  z = m*x_hat %全年预测值
16 u =sum(han1)/sum(sum(han1)) %根据历史数据计算每个月的比例值
17 v = z*u %计算每个月的预测值

结果：

ab =

-0.0993
    85.5985

x_hat =

162.8793

z =

1.9546e+03

u =

1 至 6 列

0.0794    0.0807    0.0749    0.0786    0.0819    0.0818

7 至 12 列

0.0845    0.0838    0.0872    0.0886    0.0866    0.0920

v =

1 至 6 列

155.2152  157.7365  146.4023  153.5421  160.1400  159.8337

7 至 12 列

165.0649  163.7924  170.5317  173.1473  169.3064  179.8394

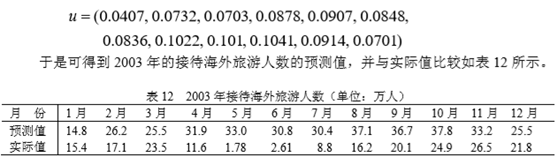
　　(2)接待海外旅游人数

　　

　　

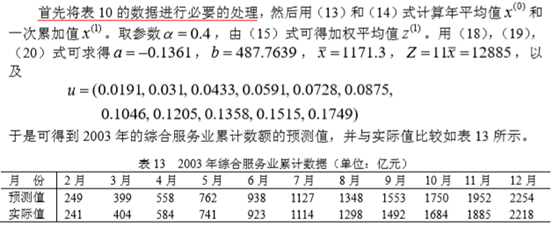
　　（3）综合服务业累计数据

　　

五、模型的结果与分析

　　根据该市的统计报告显示，2003 年 4、 5、 6 三个月的实际商品零售额分别为 145.2、 124、144.1 亿元。在这之前，根据统计部门的估计 4、5、6 三个月份 SARS 疫情对该市 的商品零售业的影响为严重，这三个月估计大约损失 62 亿元左右。从我们的模型预 测结果来计算，4、5、6 三个月的损失为 60.1 亿元，这个数基本与专家的估计值相符， 8 月基本恢复正常，这也说明了模型的正确性和可靠性。

　　对于旅游业来说是受影响严重的行业之一，严重的 4、5、6、7 四个月就损失 100 多万人，按新统计数据，平均每人消费 1002 美元计算，大约损失 10 亿美元。全 年大约损失 162 万人，约合 16.2 亿美元，到年底基本恢复正常。

　　对于综合服务业中的部分行业影响较大，如航空交通运输、宾馆餐饮等，但有些 行业影响不大，如电信、通讯等，总平均来看，影响还不算太大，5、6、7、8 四个月 大约损失 70 亿元。

　　该模型虽是就某经济指标的发展规律进行评估预测而建立的，但类似地也适用于 其它方面的一些数据规律的评估预测问题，即该模型具有很广泛的应用性。

　　不足之处：此处并没有做GM(1,1)的模型检验。