文本主题模型之非负矩阵分解(NMF)

　　　　在文本主题模型之潜在语义索引(LSI)中，我们讲到LSI主题模型使用了奇异值分解，面临着高维度计算量太大的问题。这里我们就介绍另一种基于矩阵分解的主题模型：非负矩阵分解(NMF)，它同样使用了矩阵分解，但是计算量和处理速度则比LSI快，它是怎么做到的呢？

1. 非负矩阵分解(NMF)概述

　　　　非负矩阵分解(non-negative matrix factorization，以下简称NMF)是一种非常常用的矩阵分解方法，它可以适用于很多领域，比如图像特征识别，语音识别等，这里我们会主要关注于它在文本主题模型里的运用。

　　　　回顾奇异值分解，它会将一个矩阵分解为三个矩阵：$$A = U\Sigma V^T$$

　　　　如果降维到$k$维，则表达式为：$$A_{m \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n}$$

　　　　但是NMF虽然也是矩阵分解，它却使用了不同的思路，它的目标是期望将矩阵分解为两个矩阵:$$A_{m \times n} \approx  W_{m \times k}H_{k \times n}$$

　　　　分解成两个矩阵是不是一定就比SVD省时呢？这里的理论不深究，但是NMF的确比SVD快。不过如果大家读过我写的矩阵分解在协同过滤推荐算法中的应用，就会发现里面的FunkSVD所用的算法思路和NMF基本是一致的，只不过FunkSVD聚焦于推荐算法而已。

　　　　那么如何可以找到这样的矩阵呢？这就涉及到NMF的优化思路了。

2. NMF的优化思路

　　　　NMF期望找到这样的两个矩阵$W,H$，使$WH$的矩阵乘积得到的矩阵对应的每个位置的值和原矩阵$A$对应位置的值相比误差尽可能的小。用数学的语言表示就是：$$\underbrace{arg\;min}_{W,H}\frac{1}{2}\sum\limits_{i,j}(A_{ij}-(WH)_{ij})^2$$

　　　　如果完全用矩阵表示，则为：$$\underbrace{arg\;min}_{W,H}\frac{1}{2}||A-WH||_{Fro}^2$$

　　　　其中，$ ||*||_{Fro}$为Frobenius范数。

　　　　当然对于这个式子，我们也可以加上L1和L2的正则化项如下：

　　　　$$\underbrace{arg\;min}_{W,H}\frac{1}{2}||A-WH||_{Fro}^2 +\alpha\rho|| W||_1+\alpha\rho|| H||_1+\frac{\alpha(1-\rho)}{2}|| W||_{Fro}^2 + \frac{\alpha(1-\rho)}{2}|| H||_{Fro}^2$$

　　　　其中，$\alpha$为L1&L2正则化参数，而$\rho$为L1正则化占总正则化项的比例。$||*||_1$为L1范数。

　　　　我们要求解的有$m*k + k*n$个参数。参数不少，常用的迭代方法有梯度下降法和拟牛顿法。不过如果我们决定加上了L1正则化的话就不能用梯度下降和拟牛顿法了。此时可以用坐标轴下降法或者最小角回归法来求解。scikit-learn中NMF的库目前是使用坐标轴下降法来求解的，，即在迭代时，一次固定$m*k + k*n-1$个参数，仅仅最优化一个参数。这里对优化求$W,H$的过程就不再写了，如果大家对坐标轴下降法不熟悉，参看之前写的这一篇Lasso回归算法： 坐标轴下降法与最小角回归法小结。

3. NMF 用于文本主题模型

　　　　回到我们本文的主题，NMF矩阵分解如何运用到我们的主题模型呢？

　　　　此时NMF可以这样解释：我们输入的有m个文本，n个词，而$A_{ij}$对应第i个文本的第j个词的特征值，这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数，一般要比文本数少。NMF分解后，$W_{ik}$对应第i个文本的和第k个主题的概率相关度，而$H_{kj}$对应第j个词和第k个主题的概率相关度。　　

　　　　当然也可以反过来去解释：我们输入的有m个词，n个文本，而$A_{ij}$对应第i个词的第j个文本的特征值，这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数，一般要比文本数少。NMF分解后，$W_{ik}$对应第i个词的和第k个主题的概率相关度，而$H_{kj}$对应第j个文本和第k个主题的概率相关度。

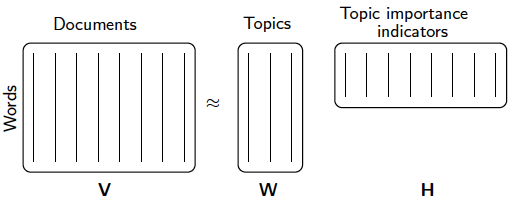
　　　　注意到这里我们使用的是"概率相关度"，这是因为我们使用的是"非负"的矩阵分解，这样我们的$W,H$矩阵值的大小可以用概率值的角度去看。从而可以得到文本和主题的概率分布关系。第二种解释用一个图来表示如下：

　　　　和LSI相比，我们不光得到了文本和主题的关系，还得到了直观的概率解释，同时分解速度也不错。当然NMF由于是两个矩阵，相比LSI的三矩阵，NMF不能解决词和词义的相关度问题。这是一个小小的代价。

4. scikit-learn NMF的使用

　　　　在 scikit-learn中，NMF在sklearn.decomposition.NMF包中，它支持L1和L2的正则化，而$W,H$的求解使用坐标轴下降法来实现。

　　　　NMF需要注意的参数有：

　　　　1） n_components：即我们的主题数k, 选择k值需要一些对于要分析文本主题大概的先验知识。可以多选择几组k的值进行NMF，然后对结果人为的进行一些验证。

　　　　2） init : 用于帮我们选择$W,H$迭代初值的算法， 默认是None,即自动选择值，不使用选择初值的算法。如果我们对收敛速度不满意，才需要关注这个值，从scikit-learn提供的算法中选择一个合适的初值选取算法。

　　　　3）alpha: 即我们第三节中的正则化参数$\alpha$,需要调参。开始建议选择一个比较小的值，如果发现效果不好在调参增大。

　　　　4) l1_ratio：　即我们第三节中的正则化参数$\rho$,L1正则化的比例，仅在$\alpha>0$时有效，需要调参。开始建议不使用，即用默认值0, 如果对L2的正则化不满意再加上L1正则化。

　　　　从上面可见，使用NMF的关键参数在于主题数的选择n_components和正则化的两个超参数$\alpha,\rho$。

　　　　此外，$W$矩阵一般在调用fit_transform方法的返回值里获得，而$H$矩阵则保存在NMF类的components_成员中。

　　　　下面我们给一个例子，我们有4个词，5个文本组成的矩阵，需要找出这些文本和隐含的两个主题之间的关系。代码如下：

　　　　完整代码参见我的github:https://github.com/ljpzzz/machinelearning/blob/master/natural-language-processing/nmf.ipynb

import numpy as np
X = np.array([[1,1,5,2,3], [0,6,2,1,1], [3, 4,0,3,1], [4, 1,5,6,3]])
from sklearn.decomposition import NMF
model = NMF(n_components=2, alpha=0.01)

　　　　现在我们看看分解得到的$W,H$：

W = model.fit_transform(X)
H = model.components_
print W
print H

　　　　结果如下：

[[ 1.67371185  0.02013017]
 [ 0.40564826  2.17004352]
 [ 0.77627836  1.5179425 ]
 [ 2.66991709  0.00940262]]
[[ 1.32014421  0.40901559  2.10322743  1.99087019  1.29852389]
 [ 0.25859086  2.59911791  0.00488947  0.37089193  0.14622829]]

　　　　从结果可以看出， 第1,3,4,5个文本和第一个隐含主题更相关，而第二个文本与第二个隐含主题更加相关。如果需要下一个结论，我们可以说，第1,3,4,5个文本属于第一个隐含主题，而第二个问题属于第2个隐含主题。

5. NMF的其他应用

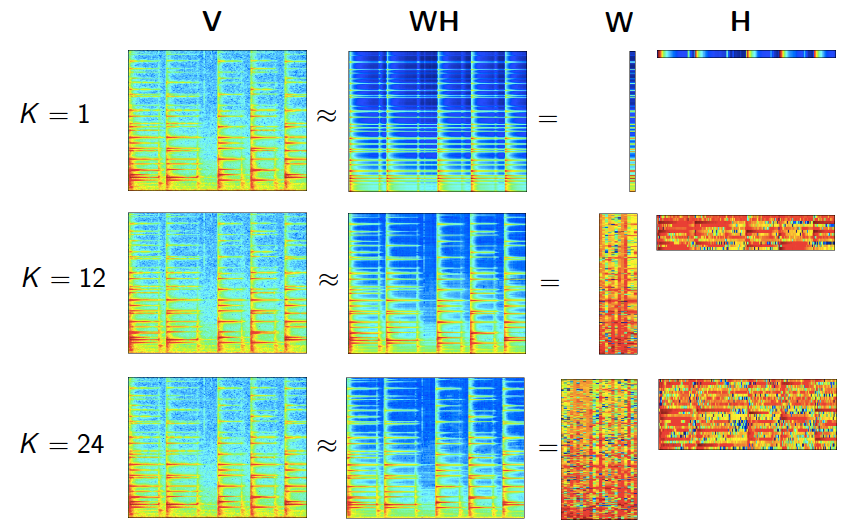
　　　　虽然我们是在主题模型里介绍的NMF，但实际上NMF的适用领域很广，除了我们上面说的图像处理，语音处理，还包括信号处理与医药工程等，是一个普适的方法。在这些领域使用NMF的关键在于将NMF套入一个合适的模型，使得$W,H$矩阵都可以有明确的意义。这里给一个图展示NMF在做语音处理时的情形：

6. NMF主题模型小结

　　　　NMF作为一个漂亮的矩阵分解方法，它可以很好的用于主题模型，并且使主题的结果有基于概率分布的解释性。但是NMF以及它的变种pLSA虽然可以从概率的角度解释了主题模型，却都只能对训练样本中的文本进行主题识别，而对不在样本中的文本是无法识别其主题的。根本原因在于NMF与pLSA这类主题模型方法没有考虑主题概率分布的先验知识，比如文本中出现体育主题的概率肯定比哲学主题的概率要高，这点来源于我们的先验知识，但是无法告诉NMF主题模型。而LDA主题模型则考虑到了这一问题，目前来说，绝大多数的文本主题模型都是使用LDA以及其变体。下一篇我们就来讨论LDA主题模型。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）