【机器学习】BP & softmax求导

目录

一、BP原理及求导

二、softmax及求导

一、BP

1、为什么沿梯度方向是上升最快方向

    根据泰勒公式对f(x)在x0处展开，得到f(x) ~ f(x0) + f'(x0)(x-x0), 故得到f(x) - f(x0) ~ f'(x0)(x-x0), 所以从x0出发，变化最快，即使f(x)-f(x0)最大，也就f'(x0)(x-x0)，由于f'(x0)与(x-x0)均为向量（现在x0取的是一个数，如果放在多维坐标那么x0就是一个多维向量），由余弦定理f'(x0) 与(x-x0)方向相同时，点积最大，故梯度方向是上升最快方向。

2、什么是BP

梯度反向传播（back propagation)过程就是： 由前馈神经网络得到损失函数，然后根据损失函数后向地更新每一层的权重，目的就是让损失函数变小

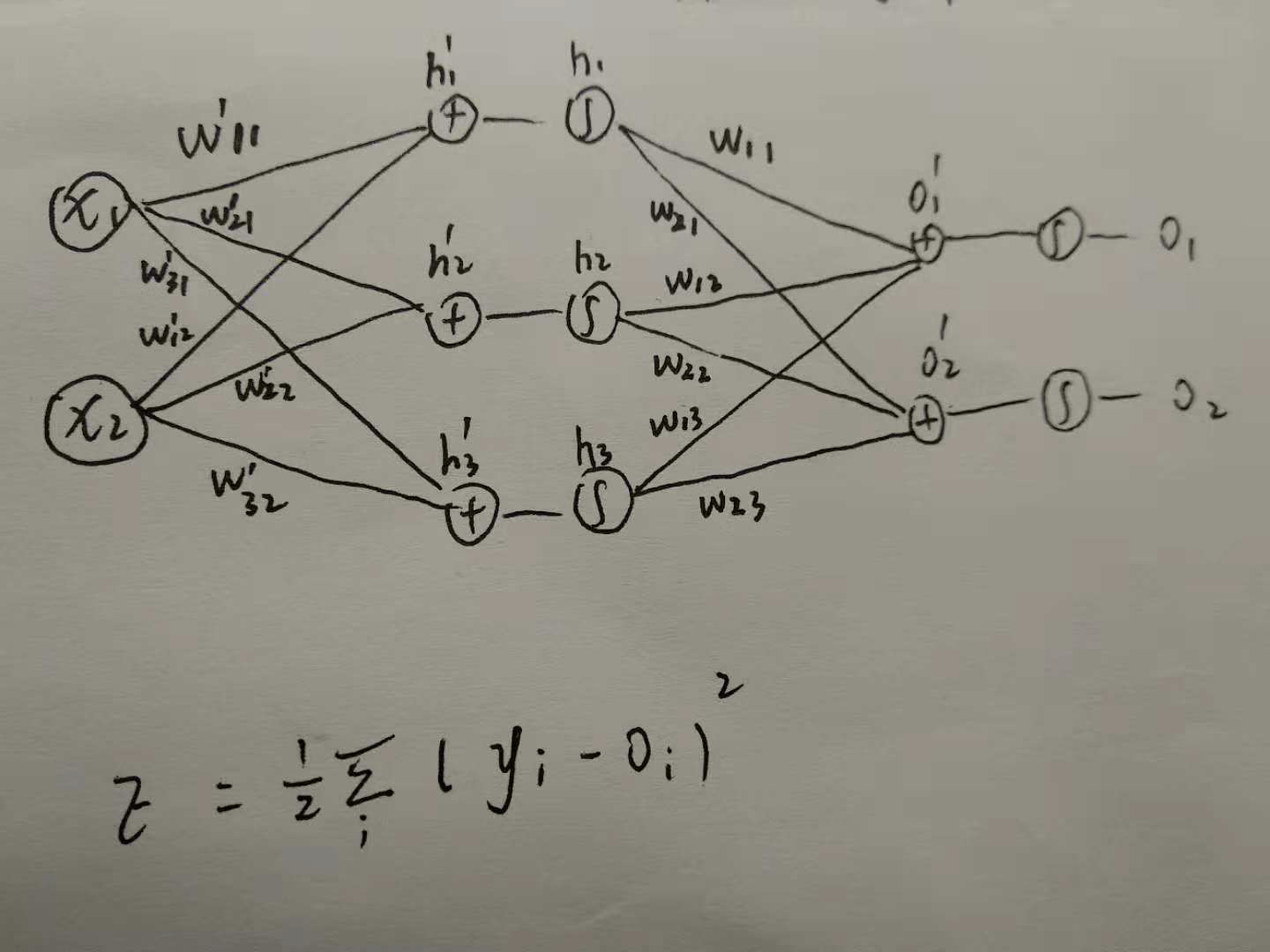
3、BP的优势

• 与从前往后进行求导相比，BP能够避开了路径被重复访问，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
• 能够自适应、自主学习。这是BP算法的根本以及其优势所在，BP算法根据预设的参数更新规则，不断地调整神经网络中的参数，以达到最符合期望的输出。

4、BP的不足

• BP是基于梯度下降算法实现的，所以容易陷入局部最小而不是全局最小
• 由于BP神经网络中的参数众多，每次都需要更新数量较多的阈值和权值，故会导致收敛速度过慢

二、softmax函数及求导

1、softmax函数

在Logistic regression二分类问题中，我们可以使用sigmoid函数将输入映射到区间中，从而得到属于某个类别的概率。将这个问题进行泛化，推广到多分类问题中，我们可以使用softmax函数，对输出的值归一化为概率值。

这里假设在进入softmax函数之前，已经有模型输出值，其中是要预测的类别数，模型可以是全连接网络的输出，其输出个数为，即输出为。

所以对每个样本，它属于类别的概率为：

通过上式可以保证 ，即属于各个类别的概率和为1。

2、求导

对softmax函数进行求导，即求 

第项的输出对第项输入的偏导。
代入softmax函数表达式，可以得到：

所以，当时：

当时：

LOSS 求导

对一个样本来说，真实类标签分布与模型预测的类标签分布可以用交叉熵来表示：

最终，对所有的样本，我们有以下loss function：

其中是样本属于类别的概率，是模型对样本预测为属于类别的概率。

对单个样本来说，loss function对输入的导数为：

上面对求导结果已经算出：

当时：

当时：

所以，将求导结果代入上式

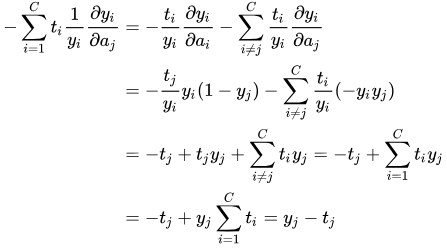
参考博客：

1、https://zhuanlan.zhihu.com/p/27223959