算法（第四版）C# 习题题解——1.4
写在前面
整个项目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
这一节内容可能会用到的库文件有 Measurement 和 TestCase，同样在 Github 上可以找到。
善用 Ctrl + F 查找题目。
习题&题解
1.4.1
解答
即为证明组合计算公式：
C(N, 3)
= N! / [(N - 3)! × 3!]
= [(N - 2) * (N - 1) * N] / 3!
= N(N - 1)(N - 2) / 6
显然 N 必须大于等于 3。
N = 3 时公式正确，只有一种组合。
N = 4 时公式正确，只有四种组合。
扩展到 N+1 个数，将 N = N + 1 代入，可得：
(N + 1)N(N - 1) / 6
N + 1 个数能组成的三位数组合可以这样理解
前 N 个数中取三个数的所有组合 +多出的一个数和前 N 个数中的任意取两个数的所有组合
即为 N(N-1)(N - 2) / 6 + C(N, 2)
变形后即为(N + 1)N(N - 1) / 6
得证。
1.4.2
解答
将 a[i] + a[j] + a[k] 改为 (long)a[i] + a[j] + a[k] 即可。
此时整个式子将按照精度最高（也就是 long）的标准计算。
long.MaxValue = 9223372036854775807 > int.MaxValue * 3 = 6442450941
代码
namespace Measurement
{
/// <summary>
/// 用暴力方法寻找数组中和为零的三元组。
/// </summary>
public static class ThreeSum
{
/// <summary>
/// 输出所有和为零的三元组。
/// </summary>
/// <param name="a">输入数组。</param>
public static void PrintAll(int[] a)
{
int n = a.Length;
for (int i = ; i < n; ++i)
{
for (int j = i + ; j < n; ++j)
{
for (int k = j + ; k < n; ++k)
{
if ((long)a[i] + a[j] + a[k] == )
{
Console.WriteLine($"{a[i]} + {a[j]} + {a[k]}");
}
}
}
}
} /// <summary>
/// 计算和为零的三元组的数量。
/// </summary>
/// <param name="a">输入数组。</param>
/// <returns></returns>
public static int Count(int[] a)
{
int n = a.Length;
int count = ;
for (int i = ; i < n; ++i)
{
for (int j = i + ; j < n; ++j)
{
for (int k = j + ; k < n; ++k)
{
if ((long)a[i] + a[j] + a[k] == )
{
count++;
}
}
}
}
return count;
}
}
}
1.4.3
解答
见代码，这里贴出绘图函数，窗体只是在得到测试结果之后简单调用以下这两个函数。
代码
public static void PaintLinear(double[] testResult)
{
//新建一个绘图窗口
Form2 linear = new Form2();
linear.Show();
//新建画布
Graphics canvas = linear.CreateGraphics();
//获取窗口区域
Rectangle rect = linear.ClientRectangle;
//计算单位长度（十等分）
int unitY = rect.Height / ;
int unitX = rect.Width / ;
//获取中心区域（上下左右增加 10% 的内补）
Rectangle center = new Rectangle(rect.X + unitX, rect.Y + unitY, unitX * , unitY * );
//绘制坐标系
canvas.DrawLine(Pens.Black, center.X, center.Y, center.X, center.Y + center.Height);
canvas.DrawLine(Pens.Black, center.X, center.Y + center.Height, center.X + center.Width, center.Y + center.Height);
//对 X 轴 10 等分，对 Y 轴 10 等分
int xaxisUnit = center.Width / ;
int yaxisUnit = center.Height / ;
//标记 X 轴坐标值
for (int i = ; i <= ; i += i)
{
canvas.DrawString(i + "N", linear.Font, Brushes.Black, center.X + i * xaxisUnit, center.Y + center.Height);
}
//反转坐标系
canvas.TranslateTransform(, linear.ClientRectangle.Height);
canvas.ScaleTransform(, -);
//计算单位长度
double Unit = center.Height / testResult[];
//标记
PointF[] result = new PointF[];
for (int i = , j = ; i < && j <= ; ++i, j += j)
{
result[i] = new PointF(center.X + j * xaxisUnit, (float)(center.Y + Unit * testResult[i]));
}
//链接
canvas.DrawLines(Pens.Black, result); canvas.Dispose();
} public static void PaintLogarithm(double[] testResult)
{
//新建一个绘图窗口
Form2 log = new Form2();
log.Show();
//新建画布
Graphics canvas = log.CreateGraphics();
//获取窗口区域
Rectangle rect = log.ClientRectangle;
//计算单位长度（十等分）
int unitY = rect.Height / ;
int unitX = rect.Width / ;
//获取中心区域（上下左右增加 10% 的内补）
Rectangle center = new Rectangle(rect.X + unitX, rect.Y + unitY, unitX * , unitY * );
//绘制坐标系
canvas.DrawLine(Pens.Black, center.X, center.Y, center.X, center.Y + center.Height);
canvas.DrawLine(Pens.Black, center.X, center.Y + center.Height, center.X + center.Width, center.Y + center.Height);
//对 X 轴 10 等分，对 Y 轴 10 等分
int xaxisUnit = center.Width / ;
int yaxisUnit = center.Height / ;
//标记 X 轴坐标值
for (int i = ; i <= ; i += i)
{
canvas.DrawString(i + "N", log.Font, Brushes.Black, center.X + i * xaxisUnit, center.Y + center.Height);
}
//反转坐标系
canvas.TranslateTransform(, log.ClientRectangle.Height);
canvas.ScaleTransform(, -);
//计算单位长度
double Unit = center.Height / testResult[];
//标记
PointF[] result = new PointF[];
for (int i = , j = ; i < && j <= ; ++i, j += j)
{
result[i] = new PointF(center.X + j * xaxisUnit, (float)(center.Y + Unit * testResult[i]));
}
//链接
canvas.DrawLines(Pens.Black, result);
canvas.Dispose();
}
1.4.4
解答
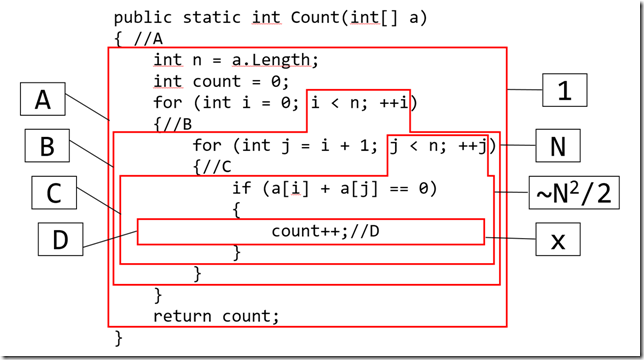
代码分块↑
时间分析↓
1.4.5
解答
类似于取极限的做法。
a. N
b. 1
c. 1
d. 2N3
e. 1
f. 2
g. N100
1.4.6
解答
a. N + N/2 + N/4 + … = ~2N，线性。
b. 1 + 2 + 4 + … = ~2N，线性。
c. logN * N，线性对数。
1.4.7
解答
最外层循环进行了 N 次比较。
次外层循环进行了 N^2 次比较。
最里层循环进行了 N^3 次比较。
内部 if 语句进行了 N^3 次比较。
if 内部进行了 N(N-1) 次加法。
加起来，~2N^3。
1.4.8
解答
平方级别：直接二层循环遍历一遍。
线性对数：只遍历一遍数组，在遍历过程中用二分查找确认在剩余数组中是否有相等的整数。
代码
/// <summary>
/// 暴力查找数组中相等的整数对。
/// </summary>
/// <param name="a">需要查找的数组。</param>
/// <returns></returns>
static int CountEqual(int[] a)
{
int n = a.Length;
int count = ;
for (int i = ; i < n; i++)
{
for (int j = i + ; j < n; j++)
{
if (a[i] == a[j])
count++;
}
} return count;
}
暴力算法↑
二分查找算法↓
/// <summary>
/// 利用 Array.Sort 进行优化的查找相等整数对算法。
/// </summary>
/// <param name="a">需要查找的数组。</param>
/// <returns></returns>
static int CountEqualLog(int[] a)
{
int n = a.Length;
int count = ;
Array.Sort(a);
int dup = ; // dup = 重复元素数量-1
for (int i = ; i < n; i++)
{
while (a[i - ] == a[i])
{
dup++;
i++;
}
count += dup * (dup + ) / ;
dup = ;
}
return count;
}
1.4.9
解答
1.4.10
解答
修改二分查找的结束条件，找到后仍然向左侧寻找，如果还能找到更小的，则返回较小的下标；否则返回当前下标。
代码
namespace _1._4._10
{
/// <summary>
/// 二分查找。
/// </summary>
public class BinarySearch
{
/// <summary>
/// 用递归方法进行二分查找。
/// </summary>
/// <param name="key">关键字。</param>
/// <param name="a">查找范围。</param>
/// <param name="lo">查找的起始下标。</param>
/// <param name="hi">查找的结束下标。</param>
/// <returns>返回下标，如果没有找到则返回 -1。</returns>
public static int Rank(int key, int[] a, int lo, int hi)
{
if (hi < lo)
return -;
int mid = (hi - lo) / + lo;
if (a[mid] == key)
{
int mini = Rank(key, a, lo, mid - );
if (mini != -)
return mini;
return mid;
}
else if (a[mid] < key)
{
return Rank(key, a, mid + , hi);
}
else
{
return Rank(key, a, lo, mid - );
}
}
}
}
1.4.11
解答
这里给出官网上的 Java 实现：StaticSETofInts.java。
howMany() 可以用二分查找实现，在找到一个值后继续向两侧查找，最后返回找到的次数。
代码
using System; namespace Measurement
{
/// <summary>
/// 有序数组，能够快速查找并自动维护其中的顺序。
/// </summary>
public class StaticSETofInts
{
private int[] a; /// <summary>
/// 用一个数组初始化有序数组。
/// </summary>
/// <param name="keys">源数组。</param>
public StaticSETofInts(int[] keys)
{
this.a = new int[keys.Length];
for (int i = ; i < keys.Length; ++i)
{
this.a[i] = keys[i];
}
Array.Sort(this.a);
} /// <summary>
/// 检查数组中是否存在指定元素。
/// </summary>
/// <param name="key">要查找的值。</param>
/// <returns>存在则返回 true，否则返回 false。</returns>
public bool Contains(int key)
{
return Rank(key, , this.a.Length - ) != -;
} /// <summary>
/// 返回某个元素在数组中存在的数量。
/// </summary>
/// <param name="key">关键值。</param>
/// <returns>返回某个元素在数组中存在的数量。</returns>
public int HowMany(int key)
{
int hi = this.a.Length - ;
int lo = ; return HowMany(key, lo, hi);
} /// <summary>
/// 返回某个元素在数组中存在的数量。
/// </summary>
/// <param name="key">关键值。</param>
/// <param name="lo">查找起始下标。</param>
/// <param name="hi">查找结束下标。</param>
/// <returns>返回某个元素在数组中存在的数量。</returns>
private int HowMany(int key, int lo, int hi)
{
int mid = Rank(key, lo, hi);
if (mid == -)
return ;
else
{
return + HowMany(key, lo, mid - ) + HowMany(key, mid + , hi);
}
} /// <summary>
/// 二分查找。
/// </summary>
/// <param name="key">关键值。</param>
/// <param name="lo">查找的起始下标。</param>
/// <param name="hi">查找的结束下标。</param>
/// <returns>返回关键值的下标，如果不存在则返回 -1。</returns>
public int Rank(int key, int lo, int hi)
{
while (lo <= hi)
{
int mid = (hi - lo) / + lo;
if (key < this.a[mid])
hi = mid - ;
else if (key > this.a[mid])
lo = mid + ;
else
return mid;
}
return -;
}
}
}
1.4.12
解答
由于两个数组都是有序的，可以同时进行比较。
设 i, j 分别为两个数组的下标。
如果 a[i] == a[j]，i 和 j 都向后移动一位。
如果 a[i] != a[j]，比较小的那个向后移动一位。
循环直到某个数组遍历完毕。
这样最后的时间复杂度 ~2N
代码
using System; namespace _1._4._12
{
/*
* 1.4.12
*
* 编写一个程序，有序打印给定的两个有序数组（含有 N 个 int 值） 中的所有公共元素，
* 程序在最坏情况下所需的运行时间应该和 N 成正比。
*
*/
class Program
{
static void Main(string[] args)
{
int[] a = new int[] { , , , };
int[] b = new int[] { , , , , , }; //2N 次数组访问，数组 a 和数组 b 各遍历一遍
for (int i = , j = ; i < a.Length && j < b.Length; )
{
if (a[i] < b[j])
{
i++;
}
else if (a[i] > b[j])
{
j++;
}
else
{
Console.WriteLine($"Common Element:{a[i]}, First index: (a[{i}], b[{j}])");
i++;
j++;
}
} }
}
}
1.4.13
解答
对象的固定开销用 Object 表示。
a. Accumulator
使用 1.2.4.3 节给出的实现。
= int * 1 + double + Object * 1
= 4 * 1 + 8 + 16 * 1 = 32
b. Transaction
= string * 1 + Date * 1 + double * 1 + Object * 1
= (40 + 16 + 4 + 4 + 2N) * 1 + (8 + 32) * 1 + 8 * 1 + 16 * 1
= 128 + 2N
c. FixedCapacityStackOfStrings
= string[] * 1 + string * N + int * 1 + Object * 1
= 24 * 1 + N * (64 + 2C) + 4 * 1 + 16 * 1
= N * (64 + 2C) + 44
= N * (64 + 2C) + 48（填充）
d.Point2D
= double * 2 + Object * 1
= 8 * 2 + 16 * 1
= 32
e.Interval1D
= double * 2 + Object * 1
= 8 * 2 + 16 * 1
= 32
f.Interval2D
= Interval1D * 2 + Object * 1
= (8 + 24) * 2 + 16 * 1
= 80
g.Double
= double * 1 + Object * 1
= 8 * 1 + 16 * 1
= 24
1.4.14
解答
这里给出暴力方法，将最内侧循环换成二分查找即为优化版本。
代码
using System; namespace Measurement
{
/// <summary>
/// 用暴力方法查找数组中和为零的四元组。
/// </summary>
public static class FourSum
{
/// <summary>
/// 输出数组中所有和为 0 的四元组。
/// </summary>
/// <param name="a">包含所有元素的数组。</param>
public static void PrintAll(long[] a)
{
int N = a.Length;
for (int i = ; i < N; ++i)
{
for (int j = i + ; j < N; ++j)
{
for (int k = j + ; k < N; ++k)
{
for (int l = k + ; l < N; ++l)
{
if (a[i] + a[j] + a[k] + a[l] == )
{
Console.WriteLine($"{a[i]} + {a[j]} + {a[k]} + {a[l]} = 0");
}
}
}
}
}
} /// <summary>
/// 计算和为零的四元组的数量。
/// </summary>
/// <param name="a">包含所有元素的数组。</param>
/// <returns></returns>
public static int Count(long[] a)
{
int N = a.Length;
int cnt = ; for (int i = ; i < N; ++i)
{
for (int j = i + ; j < N; ++j)
{
for (int k = j + ; k < N; ++k)
{
for (int l = k + ; l < N; ++l)
{
if (a[i] + a[j] + a[k] + a[l] == )
{
cnt++;
}
}
}
}
} return cnt;
}
}
}
1.4.15
解答
由于数组已经排序（从小到大），负数在左侧，正数在右侧。
TwoSumFaster
设最左侧下标为 lo，最右侧下标为 hi。
如果 a[lo] + a[hi] > 0, 说明正数太大，hi--。
如果 a[lo] + a[hi] < 0，说明负数太小，lo++。
否则就找到了一对和为零的整数对，lo++, hi--。
ThreeSumFaster
对于数组中的每一个数 a，ThreeSum 问题就等于求剩余数组中所有和为 -a 的 TwoSum 问题。
只要在 TwoSumFaster 外层再套一个循环即可。
代码
/// <summary>
/// TwoSum 的快速实现。（线性级别）
/// </summary>
/// <param name="a">需要查找的数组范围。</param>
/// <returns>数组中和为零的整数对数量。</returns>
static int TwoSumFaster(int[] a)
{
int lo = ;
int hi = a.Length - ;
int count = ;
while (lo < hi)
{
if (a[lo] + a[hi] == )
{
count++;
lo++;
hi--;
}
else if (a[lo] + a[hi] < )
{
lo++;
}
else
{
hi--;
}
}
return count;
} /// <summary>
/// ThreeSum 的快速实现。（平方级别）
/// </summary>
/// <param name="a">需要查找的数组范围。</param>
/// <returns>数组中和为零的三元组数量。</returns>
static int ThreeSumFaster(int[] a)
{
int count = ;
for (int i = ; i < a.Length; ++i)
{
int lo = i + ;
int hi = a.Length - ;
while (lo <= hi)
{
if (a[lo] + a[hi] + a[i] == )
{
count++;
lo++;
hi--;
}
else if (a[lo] + a[hi] + a[i] < )
{
lo++;
}
else
{
hi--;
}
}
}
return count;
}
1.4.16
解答
先将数组从小到大排序，再遍历一遍即可得到差距最小的两个数。
排序算法需要消耗 NlogN，具体见 MSDN：Array.Sort 方法 (Array)。
代码
using System; namespace _1._4._16
{
/*
* 1.4.16
*
* 最接近一对（一维）。
* 编写一个程序，给定一个含有 N 个 double 值的数组 a[]，
* 在其中找到一对最接近的值：两者之差（绝对值）最小的两个数。
* 程序在最坏情况下所需的运行时间应该是线性对数级别的。
*
*/
class Program
{
//总运行时间： NlogN + N = NlogN
static void Main(string[] args)
{
double[] a = new double[] { 0.1, 0.3, 0.6, 0.8, };
Array.Sort(a);//Nlog(N) 具体见 https://msdn.microsoft.com/zh-cn/library/6tf1f0bc(v=vs.110).aspx 备注部分
double minDiff = double.MaxValue;
double minA = ;
double minB = ;
for (int i = ; i < a.Length - ; ++i)//N
{
if (a[i + ] - a[i] < minDiff)
{
minA = a[i];
minB = a[i + ];
minDiff = a[i + ] - a[i];
}
}
Console.WriteLine($"Min Pair: {minA} {minB}, Min Value: {minDiff}");
}
}
}
1.4.17
解答
遍历找到最小值和最大值即可。
代码
using System; namespace _1._4._17
{
/*
* 1.4.17
*
* 最遥远的一对（一维）。
* 编写一个程序，给定一个含有 N 个 double 值的数组 a[]，
* 在其中找到一对最遥远的值：两者之差（绝对值）最大的两个数。
* 程序在最坏情况下所需的运行时间应该是线性级别的。
*
*/
class Program
{
static void Main(string[] args)
{
double[] a = new double[] { 0.1, 0.3, 0.6, 0.8, };
double min = int.MaxValue;
double max = int.MinValue; for (int i = ; i < a.Length; ++i)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
} Console.WriteLine($"MaxDiff Pair: {min} {max}, Max Difference: {Math.Abs(max - min)}");
}
}
}
1.4.18
解答
和二分查找的方式类似，先确认中间的值是否是局部最小，如果不是，则向较小的一侧二分查找。
在三个数中比较得到最小值需要两次比较，因此最坏情况下为 ~2lgN 次比较。
代码
using System; namespace _1._4._18
{
class Program
{
static void Main(string[] args)
{
var a = new int[] { , , , , };
Console.WriteLine(LocalMinimum(a));
} /// <summary>
/// 寻找数组的局部最小元素。
/// </summary>
/// <param name="a">寻找范围。</param>
/// <returns>局部最小元素的值。</returns>
static int LocalMinimum(int[] a)
{
int lo = ;
int hi = a.Length - ;
while (lo <= hi)
{
int mid = (hi - lo) / + lo;
int min = mid; // 取左中右最小值的下标
if (mid != hi && a[min] >= a[mid + ])
min = mid + ;
if (mid != lo && a[min] >= a[mid - ])
min = mid - ; if (min == mid)
return mid;
if (min > mid)
lo = min;
else
hi = min;
}
return -;
}
}
}
1.4.19
解答
算法过程类似于 “滑雪”，从数值较高的一侧向周围数值较小的一侧移动，直到到达“山谷”（局部最小）。
首先在中间行搜索最小值，再将最小值与其上下两个元素比较，如果不满足题意，则“滑向”较小的一侧，矩阵被分为了两半（上下两侧）。
在较小的一侧，找到中间列的最小值，再将最小值与其左右两个元素比较，如果不满足题意，类似的移动到较小的一侧（左右两侧）。
现在查找范围缩小到了原来矩阵的四分之一，递归的进行上述操作，最后可以得到答案。
每次查找最小值都是对行/列进行遍历，遍历耗时和 N 成正比。
代码
using System; namespace _1._4._19
{
/*
* 1.4.19
*
* 矩阵的局部最小元素。
* 给定一个含有 N^2 个不同整数的 N×N 数组 a[]。
* 设计一个运行时间和 N 成正比的算法来找出一个局部最小元素：
* 满足 a[i][j] < a[i+1][j]、a[i][j] < a[i][j+1]、a[i][j] < a[i-1][j] 以及 a[i][j] < a[i][j-1] 的索引 i 和 j。
* 程序运行时间在最坏情况下应该和 N 成正比。
*
*/
class Program
{
// 先查找 N/2 行中的最小元素，并令其与上下元素比较，
// 如果不满足题意，则向相邻的最小元素靠近再次查找
static void Main(string[] args)
{
int[,] matrix = new int[, ]
{
{ , , , , },
{ , , , , },
{ , , , , },
{ , , , , },
{ , , , , }
};
Console.WriteLine(MinimumRow(matrix, , , , ));
} /// <summary>
/// 在矩阵中间行查找局部最小。
/// </summary>
/// <param name="matrix">矩阵。</param>
/// <param name="rowStart">实际查找范围的行起始。</param>
/// <param name="rowLength">实际查找范围的行结尾。</param>
/// <param name="colStart">实际查找范围的列起始。</param>
/// <param name="colLength">实际查找范围的列结尾。</param>
/// <returns>矩阵中的局部最小元素。</returns>
static int MinimumRow(int[,] matrix, int rowStart, int rowLength, int colStart, int colLength)
{
int min = int.MaxValue;
if (rowLength < )
return int.MaxValue;
int mid = rowStart + rowLength / ;
int minCol = ;
// 获取矩阵中间行的最小值
for (int i = ; i < colLength; ++i)
{
if (min > matrix[mid, colStart + i])
{
min = matrix[mid, colStart + i];
minCol = i;
}
}
// 检查是否满足条件
if (matrix[mid, minCol] < matrix[mid - , minCol] && matrix[mid, minCol] < matrix[mid + , minCol])
{
return matrix[mid, minCol];
}
// 如果不满足则向较小一侧移动
if (matrix[mid - , minCol] > matrix[mid + , minCol])
{
return MinimumCol(matrix, rowStart, rowLength, mid + , colLength / + );
}
else
{
return MinimumCol(matrix, rowStart, rowLength, colStart, colLength / + );
}
} /// <summary>
/// 在矩阵中间列查找局部最小。
/// </summary>
/// <param name="matrix">矩阵。</param>
/// <param name="rowStart">实际查找范围的行起始。</param>
/// <param name="rowLength">实际查找范围的行结尾。</param>
/// <param name="colStart">实际查找范围的列起始。</param>
/// <param name="colLength">实际查找范围的列结尾。</param>
/// <returns>矩阵中的局部最小元素。</returns>
static int MinimumCol(int[,] matrix, int rowStart, int rowLength, int colStart, int colLength)
{
int min = int.MaxValue;
int n = matrix.GetLength();
int mid = n / ;
int minRow = ; // 获取矩阵中间列最小值
for (int i = ; i < n; ++i)
{
if (min > matrix[i, mid])
{
min = matrix[i, mid];
minRow = i;
}
}
// 检查是否满足条件
if (matrix[minRow, mid] < matrix[minRow, mid - ] && matrix[minRow, mid] < matrix[minRow, mid + ])
{
return matrix[minRow, mid];
}
// 如果不满足则向较小一侧移动
if (matrix[minRow, mid - ] > matrix[minRow, mid + ])
{
return MinimumRow(matrix, mid + , rowLength / + , colStart, colLength);
}
else
{
return MinimumRow(matrix, rowStart, rowLength / + , colStart, colLength);
}
}
}
}
1.4.20
解答
首先给出 BitMax 类的官方 Java 实现：BitonicMax.java。
我们使用这个类生成双调数组，并使用其中的 Max() 方法找到双调数组的最大值。
找到最大值之后分别对左右两侧进行二分查找，注意对于升序和降序的数组二分查找的实现有所不同。
代码
BitonicMax 类
using System; namespace _1._4._20
{
/// <summary>
/// 双调查找类。
/// </summary>
public class BitonicMax
{
/// <summary>
/// 生成双调数组。
/// </summary>
/// <param name="N">数组的大小。</param>
/// <returns></returns>
public static int[] Bitonic(int N)
{
Random random = new Random();
int mid = random.Next(N);
int[] a = new int[N];
for (int i = ; i < mid; ++i)
{
a[i] = a[i - ] + + random.Next();
} if (mid > )
{
a[mid] = a[mid - ] + random.Next() - ;
} for (int i = mid + ; i < N; ++i)
{
a[i] = a[i - ] - - random.Next();
} return a;
} /// <summary>
/// 寻找数组中的最大值。
/// </summary>
/// <param name="a">查找范围。</param>
/// <param name="lo">查找起始下标。</param>
/// <param name="hi">查找结束下标。</param>
/// <returns>返回数组中最大值的下标。</returns>
public static int Max(int[] a, int lo, int hi)
{
if (lo == hi)
{
return hi;
}
int mid = lo + (hi - lo) / ;
if (a[mid] < a[mid + ])
{
return Max(a, mid + , hi);
}
if (a[mid] > a[mid + ])
{
return Max(a, lo, mid);
}
return mid;
}
}
}
主程序
using System; namespace _1._4._20
{
/*
* 1.4.20
*
* 双调查找。
* 如果一个数组中的所有元素是先递增后递减的，则称这个数组为双调的。
* 编写一个程序，给定一个含有 N 个不同 int 值的双调数组，判断它是否含有给定的整数。
* 程序在最坏情况下所需的比较次数为 ~3lgN
*
*/
class Program
{
static void Main(string[] args)
{
int[] a = BitonicMax.Bitonic();
int max = BitonicMax.Max(a, , a.Length - );
int key = a[];
int leftside = BinarySearchAscending(a, key, , max);
int rightside = BinarySearchDescending(a, key, max, a.Length - ); if (leftside != -)
{
Console.WriteLine(leftside);
}
else if (rightside != -)
{
Console.WriteLine(rightside);
}
else
{
Console.WriteLine("No Result");
}
} /// <summary>
/// 对升序数组的二分查找。
/// </summary>
/// <param name="a">升序数组。</param>
/// <param name="key">关键值。</param>
/// <param name="lo">查找的左边界。</param>
/// <param name="hi">查找的右边界。</param>
/// <returns>返回找到关键值的下标，如果没有找到则返回 -1。</returns>
static int BinarySearchAscending(int[] a, int key, int lo, int hi)
{
while (lo <= hi)
{
int mid = lo + (hi - lo) / ; if (a[mid] < key)
{
lo = mid + ;
}
else if (a[mid] > key)
{
hi = mid - ;
}
else
{
return mid;
}
} return -;
} /// <summary>
/// 对降序数组的二分查找。
/// </summary>
/// <param name="a">升序数组。</param>
/// <param name="key">关键值。</param>
/// <param name="lo">查找的左边界。</param>
/// <param name="hi">查找的右边界。</param>
/// <returns>返回找到关键值的下标，如果没有找到则返回 -1。</returns>
static int BinarySearchDescending(int[] a, int key, int lo, int hi)
{
while (lo < hi)
{
int mid = lo + (hi - lo) / ; if (a[mid] > key)
{
lo = mid + ;
}
else if (a[mid] < key)
{
hi = mid - ;
}
else
{
return mid;
}
} return -;
}
}
}
1.4.21
解答
直接将 Contains() 实现为二分查找即可。
代码
/// <summary>
/// 检查数组中是否存在指定元素。
/// </summary>
/// <param name="key">要查找的值。</param>
/// <returns>存在则返回 true，否则返回 false。</returns>
public bool Contains(int key)
{
return Rank(key, , this.a.Length - ) != -;
} /// <summary>
/// 二分查找。
/// </summary>
/// <param name="key">关键值。</param>
/// <param name="lo">查找的起始下标。</param>
/// <param name="hi">查找的结束下标。</param>
/// <returns>返回关键值的下标，如果不存在则返回 -1。</returns>
public int Rank(int key, int lo, int hi)
{
while (lo <= hi)
{
int mid = (hi - lo) / + lo;
if (key < this.a[mid])
hi = mid - ;
else if (key > this.a[mid])
lo = mid + ;
else
return mid;
}
return -;
}
1.4.22
解答
普通二分查找是通过除法不断减半缩小搜索范围。
这里我们用斐波那契数列来缩小范围。
举个例子，例如数组大小是 100，比它大的最小斐波那契数是 144。
斐波那契数列如下：0 1 1 2 3 5 8 13 21 34 55 89 144
我们记 F(n) = 144,F(n-1) = 89, F(n-2) = 55。
我们先查看第 0 + F(n-2) 个数，如果比关键值小则直接将范围缩小到 [55, 100]；否则则在[0, 55]之间查找。
之后我们令 n = n-1。
递归上述过程即可完成查找。
代码
/// <summary>
/// 使用斐波那契数列进行的查找。
/// </summary>
/// <param name="a">查找范围。</param>
/// <param name="key">关键字。</param>
/// <returns>返回查找到的关键值下标，没有结果则返回 -1。</returns>
static int rank(int[] a, int key)
{
// 使用斐波那契数列作为缩减范围的依据
int Fk = ;
int Fk_1 = ;
int Fk_2 = ; // 获得 Fk，Fk需要大于等于数组的大小，复杂度 lgN
while (Fk < a.Length)
{
Fk = Fk + Fk_1;
Fk_1 = Fk_1 + Fk_2;
Fk_2 = Fk - Fk_1;
} int lo = ; // 按照斐波那契数列缩减查找范围，复杂度 lgN
while (Fk_2 >= )
{
int i = lo + Fk_2 > a.Length - ? a.Length - : lo + Fk_2;
if (a[i] < key)
{
lo = lo + Fk_2;
}
else if (a[i] == key)
{
return i;
}
Fk = Fk_1;
Fk_1 = Fk_2;
Fk_2 = Fk - Fk_1;
} return -;
}
1.4.23
解答
根据书中的提示，将二分查找中判断相等的条件改为两个数的差小于等于 1/N2。
代码
// 将二分查找中的相等判定条件修改为差值小于 x，其中 x = 1/N^2。
/// <summary>
/// 二分查找。
/// </summary>
/// <param name="a">查找范围。</param>
/// <param name="key">关键字。</param>
/// <returns>结果的下标，没有结果时返回 -1。</returns>
static int BinarySearch(double[] a, double key)
{
int lo = ;
int hi = a.Length - ;
double threshold = 1.0 / (a.Length * a.Length); while (lo <= hi)
{
int mid = lo + (hi - lo) / ;
if (Math.Abs(a[mid] - key) <= threshold)
{
return mid;
}
else if (a[mid] < key)
{
lo = mid + ;
}
else
{
hi = mid - ;
}
}
return -;
}
1.4.24
解答
第一问：二分查找即可。
第二问：
按照第 1, 2, 4, 8,..., 2^k 层顺序查找，一直到 2^k > F，
随后在 [2^(k - 1), 2^k] 范围中二分查找。
代码
这里建立了一个结构体用于返回测试结果：
struct testResult
{
public int F;// 找到的 F 值。
public int BrokenEggs;// 打碎的鸡蛋数。
}
用于测试的方法：
/// <summary>
/// 扔鸡蛋，没碎返回 true，碎了返回 false。
/// </summary>
/// <param name="floor">扔鸡蛋的高度。</param>
/// <returns></returns>
static bool ThrowEgg(int floor)
{
return floor <= F;
} /// <summary>
/// 第一种方案。
/// </summary>
/// <param name="a">大楼。</param>
/// <returns></returns>
static testResult PlanA(int[] a)
{
int lo = ;
int hi = a.Length - ;
int mid = ;
int eggs = ;
testResult result = new testResult(); while (lo <= hi)
{
mid = lo + (hi - lo) / ;
if (ThrowEgg(mid))
{
lo = mid + ;
}
else
{
eggs++;
hi = mid - ;
}
} result.BrokenEggs = eggs;
result.F = hi;
return result;
} /// <summary>
/// 第二种方案。
/// </summary>
/// <param name="a">大楼。</param>
/// <returns></returns>
static testResult PlanB(int[] a)
{
int lo = ;
int hi = ;
int mid = ;
int eggs = ;
testResult result = new testResult(); while (ThrowEgg(hi))
{
lo = hi;
hi *= ;
}
eggs++; if (hi > a.Length - )
{
hi = a.Length - ;
} while (lo <= hi)
{
mid = lo + (hi - lo) / ;
if (ThrowEgg(mid))
{
lo = mid + ;
}
else
{
eggs++;
hi = mid - ;
}
} result.BrokenEggs = eggs;
result.F = hi;
return result;
}
1.4.25
解答
第一问：
第一个蛋按照 √(N), 2√(N), 3√(N), 4√(N),..., √(N) * √(N) 顺序查找直至碎掉。这里扔了 k 次，k <= √(N)。
k-1√(N) ~ k√(N) 顺序查找直至碎掉，F 值就找到了。这里最多扔 √(N) 次。
第二问：
按照第 1, 3, 6, 10,..., 1/2k^2 层顺序查找，一直到 1/2k^2 > F，
随后在 [1/2k^2 - k, 1/2k^2] 范围中顺序查找。
代码
这里我们同样定义了一个结构体：
struct testResult
{
public int F;// 测试得出的 F 值
public int BrokenEggs;// 碎掉的鸡蛋数。
public int ThrowTimes;// 扔鸡蛋的次数。
}
之后是测试用的方法：
/// <summary>
/// 扔鸡蛋，没碎返回 true，碎了返回 false。
/// </summary>
/// <param name="floor">扔鸡蛋的高度。</param>
/// <returns></returns>
static bool ThrowEgg(int floor)
{
return floor <= F;
} /// <summary>
/// 第一种方案。
/// </summary>
/// <param name="a">大楼。</param>
/// <returns></returns>
static testResult PlanA(int[] a)
{
int lo = ;
int hi = ;
int eggs = ;
int throwTimes = ;
testResult result = new testResult(); while (ThrowEgg(hi))
{
throwTimes++;
lo = hi;
hi += (int)Math.Sqrt(a.Length);
}
eggs++; if (hi > a.Length - )
{
hi = a.Length - ;
} while (lo <= hi)
{
if (!ThrowEgg(lo))
{
eggs++;
break;
}
throwTimes++;
lo++;
} result.BrokenEggs = eggs;
result.F = lo - ;
result.ThrowTimes = throwTimes;
return result;
} /// <summary>
/// 第二种方案。
/// </summary>
/// <param name="a">大楼。</param>
/// <returns></returns>
static testResult PlanB(int[] a)
{
int lo = ;
int hi = ;
int eggs = ;
int throwTimes = ;
testResult result = new testResult(); for (int i = ; ThrowEgg(hi); ++i)
{
throwTimes++;
lo = hi;
hi += i;
}
eggs++; if (hi > a.Length - )
{
hi = a.Length - ;
} while (lo <= hi)
{
if (!ThrowEgg(lo))
{
eggs++;
break;
}
lo++;
throwTimes++;
} result.BrokenEggs = eggs;
result.F = lo - ;
result.ThrowTimes = throwTimes;
return result;
}
1.4.26
解答
1.4.27
解答
实现比较简单，想象两个栈背靠背接在一起，左侧栈负责出队，右侧栈负责入队。
当左侧栈为空时就把右侧栈中的元素倒到左侧栈，这个过程是 O(n) 的。
但在这个过程之前必然有 n 个元素入栈，均摊后即为 O(1)。
代码
namespace _1._4._27
{
/// <summary>
/// 用两个栈模拟的队列。
/// </summary>
/// <typeparam name="Item">队列中的元素。</typeparam>
class StackQueue<Item>
{
Stack<Item> H;//用于保存出队元素
Stack<Item> T;//用于保存入队元素 /// <summary>
/// 构造一个队列。
/// </summary>
public StackQueue()
{
this.H = new Stack<Item>();
this.T = new Stack<Item>();
} /// <summary>
/// 将栈 T 中的元素依次弹出并压入栈 H 中。
/// </summary>
private void Reverse()
{
while (!this.T.IsEmpty())
{
this.H.Push(this.T.Pop());
}
} /// <summary>
/// 将一个元素出队。
/// </summary>
/// <returns></returns>
public Item Dequeue()
{
//如果没有足够的出队元素，则将 T 中的元素移动过来
if (this.H.IsEmpty())
{
Reverse();
} return this.H.Pop();
} /// <summary>
/// 将一个元素入队。
/// </summary>
/// <param name="item">要入队的元素。</param>
public void Enqueue(Item item)
{
this.T.Push(item);
}
}
}
1.4.28
解答
每次入队的时候将队列倒转，这样入队的元素就是第一个了。
代码
namespace _1._4._28
{
/// <summary>
/// 用一条队列模拟的栈。
/// </summary>
/// <typeparam name="Item">栈中保存的元素。</typeparam>
class QueueStack<Item>
{
Queue<Item> queue; /// <summary>
/// 初始化一个栈。
/// </summary>
public QueueStack()
{
this.queue = new Queue<Item>();
} /// <summary>
/// 向栈中添加一个元素。
/// </summary>
/// <param name="item"></param>
public void Push(Item item)
{
this.queue.Enqueue(item);
int size = this.queue.Size();
// 倒转队列
for (int i = ; i < size - ; ++i)
{
this.queue.Enqueue(this.queue.Dequeue());
}
} /// <summary>
/// 从栈中弹出一个元素。
/// </summary>
/// <returns></returns>
public Item Pop()
{
return this.queue.Dequeue();
} /// <summary>
/// 确定栈是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.queue.IsEmpty();
}
}
}
1.4.29
解答
和用两个栈实现队列的方法类似。
push 的时候把右侧栈内容倒到左侧栈，之后再入栈。
pop 的时候也做相同操作，右侧栈内容进左侧栈，之后再出栈。
enqueue 的时候则将左侧栈内容倒到右侧栈，之后再入队。
代码
namespace _1._4._29
{
/// <summary>
/// 用两个栈模拟的 Steque。
/// </summary>
/// <typeparam name="Item">Steque 中的元素类型。</typeparam>
class StackSteque<Item>
{
Stack<Item> H;
Stack<Item> T; /// <summary>
/// 初始化一个 Steque
/// </summary>
public StackSteque()
{
this.H = new Stack<Item>();
this.T = new Stack<Item>();
} /// <summary>
/// 向栈中添加一个元素。
/// </summary>
/// <param name="item"></param>
public void Push(Item item)
{
ReverseT();
this.H.Push(item);
} /// <summary>
/// 将 T 中的元素弹出并压入到 H 中。
/// </summary>
private void ReverseT()
{
while (!this.T.IsEmpty())
{
this.H.Push(this.T.Pop());
}
} /// <summary>
/// 将 H 中的元素弹出并压入到 T 中。
/// </summary>
private void ReverseH()
{
while (!this.H.IsEmpty())
{
this.T.Push(this.H.Pop());
}
} /// <summary>
/// 从 Steque 中弹出一个元素。
/// </summary>
/// <returns></returns>
public Item Pop()
{
ReverseT();
return this.H.Pop();
} /// <summary>
/// 在 Steque 尾部添加一个元素。
/// </summary>
/// <param name="item"></param>
public void Enqueue(Item item)
{
ReverseH();
this.T.Push(item);
} /// <summary>
/// 检查 Steque 是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.H.IsEmpty() && this.T.IsEmpty();
}
}
}
1.4.30
解答
steque 作为队列的头部，stack 作为队列的尾部。
pushLeft：直接 push 到 steque 中即可。
pushRight：如果 stack 为空，则直接 enqueue 到 steque 中，否则就 push 到 stack 中。
popLeft：如果 steque 为空，则将 stack 中的元素倒到 steque 中去（steque.push(stack.pop())），然后再从 steque 中 pop。
popRight：如果 stack 为空，则将 steque 中的元素倒到 stack 中去，然后再从 stack 中 pop。
代码
namespace _1._4._30
{
/// <summary>
/// 用一个栈和一个 Steque 模拟的双向队列。
/// </summary>
/// <typeparam name="Item">双向队列中保存的元素类型。</typeparam>
class Deque<Item>
{
Stack<Item> stack;//代表队列尾部
Steque<Item> steque;//代表队列头部 /// <summary>
/// 创建一条空的双向队列。
/// </summary>
public Deque()
{
this.stack = new Stack<Item>();
this.steque = new Steque<Item>();
} /// <summary>
/// 在左侧插入一个新元素。
/// </summary>
/// <param name="item">要插入的元素。</param>
public void PushLeft(Item item)
{
this.steque.Push(item);
} /// <summary>
/// 将栈中的内容移动到 Steque 中。
/// </summary>
private void StackToSteque()
{
while (!this.stack.IsEmpty())
{
this.steque.Push(this.stack.Pop());
}
} /// <summary>
/// 将 Steque 中的内容移动到栈中。
/// </summary>
private void StequeToStack()
{
while (!this.steque.IsEmpty())
{
this.stack.Push(this.steque.Pop());
}
} /// <summary>
/// 从双向队列左侧弹出一个元素。
/// </summary>
/// <returns></returns>
public Item PopLeft()
{
if (this.steque.IsEmpty())
{
StackToSteque();
}
return this.steque.Pop();
} /// <summary>
/// 向双向队列右侧添加一个元素。
/// </summary>
/// <param name="item">要插入的元素。</param>
public void PushRight(Item item)
{
if (this.stack.IsEmpty())
{
this.steque.Enqueue(item);
}
else
{
this.stack.Push(item);
}
} /// <summary>
/// 从双向队列右侧弹出一个元素。
/// </summary>
/// <returns></returns>
public Item PopRight()
{
if (this.stack.IsEmpty())
{
StequeToStack();
}
return this.stack.Pop();
} /// <summary>
/// 判断队列是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.stack.IsEmpty() && this.steque.IsEmpty();
} /// <summary>
/// 返回队列中元素的数量。
/// </summary>
/// <returns></returns>
public int Size()
{
return this.stack.Size() + this.steque.Size();
}
}
}
1.4.31
解答
三个栈分别命名为左中右。
左侧栈和右侧栈负责模拟队列，和用两个栈模拟队列的方法类似。
由于是双向队列，左栈和右栈会频繁的倒来倒去，因此每次都只倒一半的元素可以有效减少开销。
有一侧栈为空时，另一侧栈中上半部分先移动到中间栈中，下半部分倒到另一侧栈里，再从中间栈拿回上半部分元素。
这样可以确保接下来的 pop 操作一定是常数级别的。
代码
namespace _1._4._31
{
/// <summary>
/// 用三个栈模拟的双向队列。
/// </summary>
/// <typeparam name="Item">双向队列中的元素。</typeparam>
class Deque<Item>
{
Stack<Item> left;
Stack<Item> middle;
Stack<Item> right; /// <summary>
/// 构造一条新的双向队列。
/// </summary>
public Deque()
{
this.left = new Stack<Item>();
this.middle = new Stack<Item>();
this.right = new Stack<Item>();
} /// <summary>
/// 向双向队列左侧插入一个元素。
/// </summary>
/// <param name="item">要插入的元素。</param>
public void PushLeft(Item item)
{
this.left.Push(item);
} /// <summary>
/// 向双向队列右侧插入一个元素。
/// </summary>
/// <param name="item">要插入的元素。</param>
public void PushRight(Item item)
{
this.right.Push(item);
} /// <summary>
/// 当一侧栈为空时，将另一侧的下半部分元素移动过来。
/// </summary>
/// <param name="source">不为空的栈。</param>
/// <param name="destination">空栈。</param>
private void Move(Stack<Item> source, Stack<Item> destination)
{
int n = source.Size();
// 将上半部分元素移动到临时栈 middle
for (int i = ; i < n / ; ++i)
{
this.middle.Push(source.Pop());
}
// 将下半部分移动到另一侧栈中
while (!source.IsEmpty())
{
destination.Push(source.Pop());
}
// 从 middle 取回上半部分元素
while (!this.middle.IsEmpty())
{
source.Push(this.middle.Pop());
}
} /// <summary>
/// 检查双端队列是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.right.IsEmpty() && this.middle.IsEmpty() && this.left.IsEmpty();
} /// <summary>
/// 从右侧弹出一个元素。
/// </summary>
/// <returns></returns>
public Item PopRight()
{
if (this.right.IsEmpty())
{
Move(this.left, this.right);
} return this.right.Pop();
} /// <summary>
/// 从左侧弹出一个元素。
/// </summary>
/// <returns></returns>
public Item PopLeft()
{
if (this.left.IsEmpty())
{
Move(this.right, this.left);
} return this.left.Pop();
} /// <summary>
/// 返回双端队列的大小。
/// </summary>
/// <returns></returns>
public int Size()
{
return this.left.Size() + this.middle.Size() + this.right.Size();
}
}
}
1.4.32
解答
首先，不需要扩容数组的的操作都只需访问数组一次，M 次操作就是 M 次访问。
随后我们有性质， M 次栈操作后额外复制访问数组的次数小于 2M。
这里简单证明，设 M 次操作之后栈的大小为 n，那么额外访问数组的次数为：
S = n/2 + n/4 + n/8 +...+ 2 < n
为了能使栈大小达到 n，M 必须大于等于 n/2
因此 2M >= n > S，得证。
因此我们可以得到 M 次操作后访问数组次数的总和 S' = S + M < 3M
1.4.33
解答
Integer = 4(int) + 8(对象开销) = 12
Date = 3 * 4(int * 3) + 8(对象开销) = 20
Counter = 4(String 的引用) + 4(int) + 8(对象开销) = 16
int[] = 8(对象开销) + 4(数组长度) + 4N = 12 + 4N
double[] = 8(对象开销) + 4(数组长度) + 8N = 12 + 8N
double[][] = 8(对象开销) + 4(数组长度) + 4M(引用) + M(12 + 8N)(M 个一维数组) = 12 + 16M + 8MN
String = 8(对象开销) + 3*4(int * 3) + 4(字符数组的引用) = 24
Node = 8(对象开销) + 4*2(引用*2) = 16
Stack = 8(对象开销) + 4(引用) + 4(int) = 16
1.4.34
解答
1. 第一种方案，类似于二分查找，先猜测左边界(lo)，再猜测右边界(hi)，如果边界值猜中的话直接返回，否则：
如果右边界比较热，那么左边界向右边界靠，lo=mid；否则，右边界向左边界靠，hi=mid。其中，mid = lo + (hi – lo)/2。
每次二分查找都要猜测两次，~2lgN。
2. 第二种方案，假设上次猜测值为 lastGuess，本次即将要猜测的值为 nowGuess，通过方程：
(lastGuess + nowGuess)/2 = (lo + hi)/2
可以求得 nowGuess，具体可以查看示意图：
数字是猜测顺序，黑色范围是猜测值的范围（lastGuess 和 nowGuess），绿色的是实际查找的范围（lo 和 hi）。
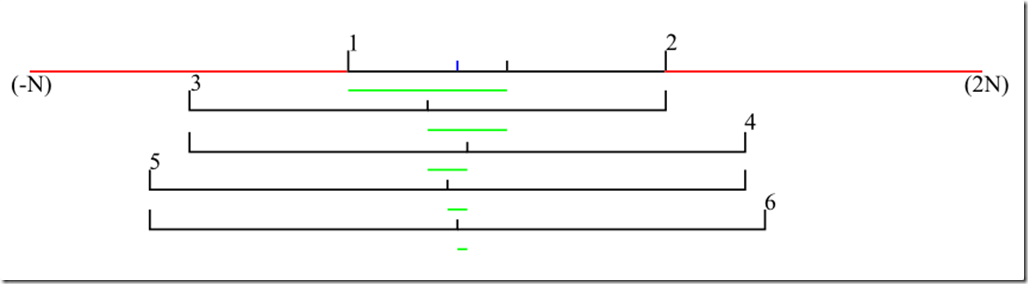
代码
首先是 Game 类
using System; namespace _1._4._34
{
/// <summary>
/// 某次猜测的结果。
/// </summary>
enum GuessResult
{
Hot = , // 比上次猜测更接近目标。
Equal = , // 猜中目标。
Cold = -, // 比上次猜测更远离目标。
FirstGuess = - // 第一次猜测。
} /// <summary>
/// 游戏类。
/// </summary>
class Game
{
public int N { get; } // 目标值的最大范围。
public int SecretNumber { get; } // 目标值。
public int LastGuess { get; private set; } // 上次猜测的值 /// <summary>
/// 构造函数，新开一局游戏。
/// </summary>
/// <param name="N">目标值的最大范围。</param>
public Game(int N)
{
Random random = new Random();
this.N = N;
this.SecretNumber = random.Next(N - ) + ;
this.LastGuess = -;
} /// <summary>
/// 猜测，根据与上次相比更为接近还是远离目标值返回结果。
/// </summary>
/// <param name="guess">本次的猜测值</param>
/// <returns>接近或不变返回 Hot，远离则返回 Cold，猜中返回 Equal。</returns>
public GuessResult Guess(int guess)
{
if (guess == this.SecretNumber)
{
return GuessResult.Equal;
}
if (this.LastGuess == -)
{
this.LastGuess = guess;
return GuessResult.FirstGuess;
} int lastDiff = Math.Abs(this.LastGuess - this.SecretNumber);
this.LastGuess = guess;
int nowDiff = Math.Abs(guess - this.SecretNumber);
if (nowDiff > lastDiff)
{
return GuessResult.Cold;
}
else
{
return GuessResult.Hot;
}
} /// <summary>
/// 重置游戏，清空上次猜测的记录。目标值和最大值都不变。
/// </summary>
public void Restart()
{
this.LastGuess = -;
}
}
}
之后是实际测试的方法：
using System; namespace _1._4._34
{
/*
* 1.4.34
*
* 热还是冷。
* 你的目标是猜出 1 到 N 之间的一个秘密的整数。
* 每次猜完一个整数后，你会直到你的猜测距离该秘密整数是否相等（如果是则游戏结束）。
* 如果不相等，你会知道你的猜测相比上一次猜测距离秘密整数是比较热（接近），还是比较冷（远离）。
* 设计一个算法在 ~2lgN 之内找到这个秘密整数，然后设计一个算法在 ~1lgN 之内找到这个秘密整数。
*
*/
class Program
{
/// <summary>
/// 某种方案的测试结果，包含猜测结果和尝试次数。
/// </summary>
struct TestResult
{
public int SecretNumber;// 猜测到的数字。
public int TryTimes;// 尝试次数。
} static void Main(string[] args)
{
Game game = new Game();
TestResult A = PlayGameA(game);
game.Restart();
TestResult B = PlayGameB(game); Console.WriteLine($"SecretNumber:{game.SecretNumber}");
Console.WriteLine("TestResultA:");
Console.WriteLine($"SecretNumber:{A.SecretNumber}, TryTimes:{A.TryTimes}");
Console.WriteLine();
Console.WriteLine("TestResultB:");
Console.WriteLine($"SecretNumber:{B.SecretNumber}, TryTimes:{B.TryTimes}");
} /// <summary>
/// 方案一，用二分查找实现，需要猜测 2lgN 次。
/// </summary>
/// <param name="game">用于猜测的游戏对象。</param>
/// <returns>返回测试结果，包含猜测结果和尝试次数。</returns>
static TestResult PlayGameA(Game game)
{
TestResult result;
result.TryTimes = ;
result.SecretNumber = ;
GuessResult guessResult; int hi = game.N;
int lo = ; // 利用二分查找猜测，2lgN
while (lo <= hi)
{
int mid = lo + (hi - lo) / ; guessResult = game.Guess(lo);
result.TryTimes++;
if (guessResult == GuessResult.Equal)
{
result.SecretNumber = lo;
return result;
} guessResult = game.Guess(hi);
result.TryTimes++;
if (guessResult == GuessResult.Equal)
{
result.SecretNumber = hi;
return result;
}
else if (guessResult == GuessResult.Hot)
{
lo = mid;
}
else
{
hi = mid;
}
} return result;
} /// <summary>
/// 方案二，根据 (lastGuess + nowGuess)/2 = (lo + hi) / 2 确定每次猜测的值。
/// </summary>
/// <param name="game">用于猜测的游戏对象。</param>
/// <returns>返回测试结果，包含猜测结果和尝试次数。</returns>
static TestResult PlayGameB(Game game)
{
TestResult result;
result.TryTimes = ;
result.SecretNumber = ;
GuessResult guessResult; int hi = game.N;
int lo = ;
bool isRightSide = true; // 第一次猜测
guessResult = game.Guess();
result.TryTimes++;
if (guessResult == GuessResult.Equal)
{
result.SecretNumber = ;
return result;
} while (lo < hi)
{
int mid = lo + (hi - lo) / ;
int nowGuess = (lo + hi) - game.LastGuess; guessResult = game.Guess(nowGuess);
result.TryTimes++;
if (guessResult == GuessResult.Equal)
{
result.SecretNumber = nowGuess;
break;
}
else if (guessResult == GuessResult.Hot)
{
if (isRightSide)
{
lo = mid;
}
else
{
hi = mid;
}
}
else
{
if (isRightSide)
{
hi = mid;
}
else
{
lo = mid;
}
}
isRightSide = !isRightSide;
if (hi - lo <= )
{
break;
}
}
if (game.Guess(lo) == GuessResult.Equal)
{
result.TryTimes++;
result.SecretNumber = lo;
}
else if (game.Guess(hi) == GuessResult.Equal)
{
result.TryTimes++;
result.SecretNumber = hi;
} return result;
}
}
}
1.4.35
解答
1. 一个 Node 对象包含一个 int(泛型 Item) 的引用和下一个 Node 对象的引用。push 操作创建新 Node 对象时会创建一个引用。
因此对于第一种情况，压入 n 个 int 类型的元素创建了 N 个 Node 对象，创建了 2N 个引用。
2. 比起上一种情况，每个 Node 对象多包含了一个指向 Integer 的引用。
因此对于第二中情况，压入 n 个 int 类型的元素创建了 N 个 Node 对象和 N 个 Integer 对象，比起第一种情况多创建了 N 个引用。
3. 对于数组来说，创建对象只有扩容时重新创建数组对象一种情况，对于 N 次 push 操作只需要 lgN 次扩容，因此创建的对象为 lgN 个。
每次扩容都需要重新创建引用，(4 + 8 +...+ 2N)(扩容) + N(每次 push 操作) = 5N - 4 = ~5N
4. 创建引用和上题一样，创建对象则多出了装箱过程，每次 push 都会新建一个 Integer 对象，N + lgN = ~N。
1.4.36
解答
1. N 个 Node<int> 对象的空间开销
= N * (16(对象开销) + 4(int) + 8(下一个 Node 的引用) + 4(填充字节)) = 32N
2. 比起上一题来说，空间开销变为
= N * (16(Node 对象开销) + 8(Integer 对象引用) + (16(Integer 对象开销) + 4(int) + 4(填充字节)) + 8(下一个对象的引用) = 32N + 24N = 56N。
3. 如果不扩容则是 4N，N 个元素最多可以维持 4N 的栈空间（少于四分之一将缩小）。
4. 比起上一题，数组元素变成了引用每个占用 8 字节，还要额外加上 Integer 对象的每个 24 字节。
= (8 + 24)N ~ (8 * 4 + 24)N
1.4.37
解答
数据量比较大时才会有比较明显的差距。
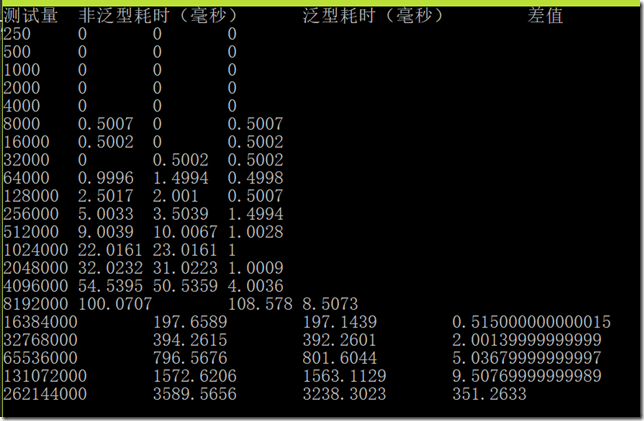
代码
FixedCapacityStackOfInts，根据 FixedCapacityOfString 修改而来：
using System;
using System.Collections;
using System.Collections.Generic; namespace _1._4._37
{
/// <summary>
/// 固定大小的整型数据栈。
/// </summary>
class FixedCapacityStackOfInts : IEnumerable<int>
{
private int[] a;
private int N; /// <summary>
/// 默认构造函数。
/// </summary>
/// <param name="capacity">栈的大小。</param>
public FixedCapacityStackOfInts(int capacity)
{
this.a = new int[capacity];
this.N = ;
} /// <summary>
/// 检查栈是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.N == ;
} /// <summary>
/// 检查栈是否已满。
/// </summary>
/// <returns></returns>
public bool IsFull()
{
return this.N == this.a.Length;
} /// <summary>
/// 将一个元素压入栈中。
/// </summary>
/// <param name="item">要压入栈中的元素。</param>
public void Push(int item)
{
this.a[this.N] = item;
this.N++;
} /// <summary>
/// 从栈中弹出一个元素，返回被弹出的元素。
/// </summary>
/// <returns></returns>
public int Pop()
{
this.N--;
return this.a[this.N];
} /// <summary>
/// 返回栈顶元素（但不弹出它）。
/// </summary>
/// <returns></returns>
public int Peek()
{
return this.a[this.N - ];
} public IEnumerator<int> GetEnumerator()
{
return new ReverseEnmerator(this.a);
} IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
} private class ReverseEnmerator : IEnumerator<int>
{
private int current;
private int[] a; public ReverseEnmerator(int[] a)
{
this.current = a.Length;
this.a = a;
} int IEnumerator<int>.Current => this.a[this.current]; object IEnumerator.Current => this.a[this.current]; void IDisposable.Dispose()
{
this.current = -;
this.a = null;
} bool IEnumerator.MoveNext()
{
if (this.current == )
return false;
this.current--;
return true;
} void IEnumerator.Reset()
{
this.current = this.a.Length;
}
}
}
}
FixedCapacityStack<Item>
using System;
using System.Collections;
using System.Collections.Generic; namespace _1._4._37
{
/// <summary>
/// 固定大小的栈。
/// </summary>
class FixedCapacityStack<Item> : IEnumerable<Item>
{
private Item[] a;
private int N; /// <summary>
/// 默认构造函数。
/// </summary>
/// <param name="capacity">栈的大小。</param>
public FixedCapacityStack(int capacity)
{
this.a = new Item[capacity];
this.N = ;
} /// <summary>
/// 检查栈是否为空。
/// </summary>
/// <returns></returns>
public bool IsEmpty()
{
return this.N == ;
} /// <summary>
/// 检查栈是否已满。
/// </summary>
/// <returns></returns>
public bool IsFull()
{
return this.N == this.a.Length;
} /// <summary>
/// 将一个元素压入栈中。
/// </summary>
/// <param name="item">要压入栈中的元素。</param>
public void Push(Item item)
{
this.a[this.N] = item;
this.N++;
} /// <summary>
/// 从栈中弹出一个元素，返回被弹出的元素。
/// </summary>
/// <returns></returns>
public Item Pop()
{
this.N--;
return this.a[this.N];
} /// <summary>
/// 返回栈顶元素（但不弹出它）。
/// </summary>
/// <returns></returns>
public Item Peek()
{
return this.a[this.N - ];
} public IEnumerator<Item> GetEnumerator()
{
return new ReverseEnmerator(this.a);
} IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
} private class ReverseEnmerator : IEnumerator<Item>
{
private int current;
private Item[] a; public ReverseEnmerator(Item[] a)
{
this.current = a.Length;
this.a = a;
} Item IEnumerator<Item>.Current => this.a[this.current]; object IEnumerator.Current => this.a[this.current]; void IDisposable.Dispose()
{
this.current = -;
this.a = null;
} bool IEnumerator.MoveNext()
{
if (this.current == )
return false;
this.current--;
return true;
} void IEnumerator.Reset()
{
this.current = this.a.Length;
}
}
}
}
测试函数：
using System;
using Measurement; namespace _1._4._37
{
/// <summary>
/// FixedCapacityStackOfInts 测试类。
/// </summary>
public static class DoubleTest
{
private static readonly int MAXIMUM_INTEGER = ; /// <summary>
/// 返回对 n 个随机整数的栈进行 n 次 push 和 n 次 pop 所需的时间。
/// </summary>
/// <param name="n">随机数组的长度。</param>
/// <returns></returns>
public static double TimeTrial(int n)
{
int[] a = new int[n];
FixedCapacityStackOfInts stack = new FixedCapacityStackOfInts(n);
Random random = new Random(DateTime.Now.Millisecond);
for (int i = ; i < n; ++i)
{
a[i] = random.Next(-MAXIMUM_INTEGER, MAXIMUM_INTEGER);
}
Stopwatch timer = new Stopwatch();
for (int i = ; i < n; ++i)
{
stack.Push(a[i]);
}
for (int i = ; i < n; ++i)
{
stack.Pop();
}
return timer.ElapsedTimeMillionSeconds();
} /// <summary>
/// 返回对 n 个随机整数的栈进行 n 次 push 和 n 次 pop 所需的时间。
/// </summary>
/// <param name="n">随机数组的长度。</param>
/// <returns></returns>
public static double TimeTrialGeneric(int n)
{
int[] a = new int[n];
FixedCapacityStack<int> stack = new FixedCapacityStack<int>(n);
Random random = new Random(DateTime.Now.Millisecond);
for (int i = ; i < n; ++i)
{
a[i] = random.Next(-MAXIMUM_INTEGER, MAXIMUM_INTEGER);
}
Stopwatch timer = new Stopwatch();
for (int i = ; i < n; ++i)
{
stack.Push(a[i]);
}
for (int i = ; i < n; ++i)
{
stack.Pop();
}
return timer.ElapsedTimeMillionSeconds();
}
}
}
主函数：
using System; namespace _1._4._37
{
/*
* 1.4.37
*
* 自动装箱的性能代价。
* 通过实验在你的计算机上计算使用自动装箱所付出的性能代价。
* 实现一个 FixedCapacityStackOfInts，
* 并使用类似 DoublingRatio 的用例比较它和泛型 FixedCapacityStack 在进行大量 push() 和 pop() 时的性能。
*
*/
class Program
{
static void Main(string[] args)
{
Console.WriteLine("测试量\t非泛型耗时（毫秒）\t泛型耗时（毫秒）\t差值");
for (int n = ; true; n += n)
{
double time = DoubleTest.TimeTrial(n);
double timeGeneric = DoubleTest.TimeTrialGeneric(n);
Console.WriteLine($"{n}\t{time}\t{timeGeneric}\t{Math.Abs(time - timeGeneric)}");
}
}
}
}
1.4.38
解答
把 DoublingTest 中调用的函数稍作修改即可。
代码
ThreeSum 测试类
using System; namespace _1._4._38
{
/// <summary>
/// ThreeSum 测试类。
/// </summary>
public static class DoubleTest
{
private static readonly int MAXIMUM_INTEGER = ; /// <summary>
/// 返回对 n 个随机整数的数组进行一次 ThreeSum 所需的时间。
/// </summary>
/// <param name="n">随机数组的长度。</param>
/// <returns></returns>
public static double TimeTrial(int n)
{
int[] a = new int[n];
Random random = new Random(DateTime.Now.Millisecond);
for (int i = ; i < n; ++i)
{
a[i] = random.Next(-MAXIMUM_INTEGER, MAXIMUM_INTEGER);
}
Measurement.Stopwatch timer = new Measurement.Stopwatch();
ThreeSum.Count(a);
return timer.ElapsedTime();
}
}
}
ThreeSum
using System; namespace _1._4._38
{
/// <summary>
/// 用暴力方法寻找数组中和为零的三元组。
/// </summary>
public static class ThreeSum
{
/// <summary>
/// 输出所有和为零的三元组。
/// </summary>
/// <param name="a">输入数组。</param>
public static void PrintAll(int[] a)
{
int n = a.Length;
for (int i = ; i < n; ++i)
{
for (int j = ; j < n; ++j)
{
for (int k = ; k < n; ++k)
{
if (i < j && j < k)
{
if ((long)a[i] + a[j] + a[k] == )
{
Console.WriteLine($"{a[i]} + {a[j]} + {a[k]}");
}
}
}
}
}
} /// <summary>
/// 计算和为零的三元组的数量。
/// </summary>
/// <param name="a">输入数组。</param>
/// <returns></returns>
public static int Count(int[] a)
{
int n = a.Length;
int count = ;
for (int i = ; i < n; ++i)
{
for (int j = ; j < n; ++j)
{
for (int k = ; k < n; ++k)
{
if (i < j && j < k)
{
if ((long)a[i] + a[j] + a[k] == )
{
count++;
}
}
}
}
}
return count;
}
}
}
1.4.39
解答
执行 N 次后取平均即可。
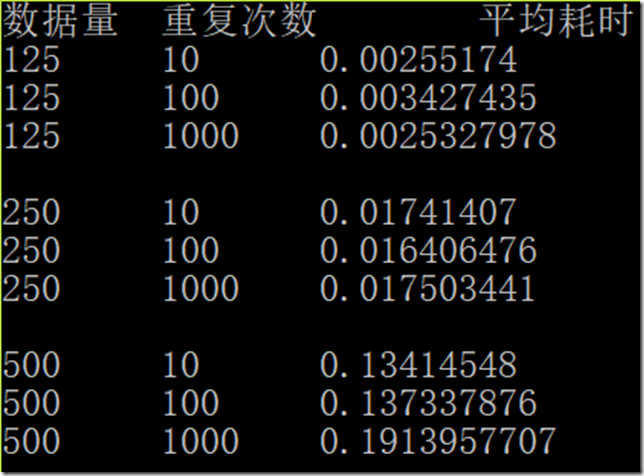
代码
修改后的 DoublingTest：
using System;
using Measurement; namespace _1._4._39
{
/// <summary>
/// ThreeSum 测试类。
/// </summary>
public static class DoubleTest
{
private static readonly int MAXIMUM_INTEGER = ; /// <summary>
/// 返回对 n 个随机整数的数组进行一次 ThreeSum 所需的时间。
/// </summary>
/// <param name="n">随机数组的长度。</param>
/// <param name="repeatTimes">重复测试的次数。</param>
/// <returns></returns>
public static double TimeTrial(int n, int repeatTimes)
{
int[] a = new int[n];
double sum = ;
Random random = new Random(DateTime.Now.Millisecond);
for (int i = ; i < n; ++i)
{
a[i] = random.Next(-MAXIMUM_INTEGER, MAXIMUM_INTEGER);
}
for (int i = ; i < repeatTimes; ++i)
{
Stopwatch timer = new Stopwatch();
ThreeSum.Count(a);
sum += timer.ElapsedTime();
}
return sum / repeatTimes;
}
}
}
1.4.40
解答
N 个数可组成的三元组的总数为：
C(N, 3) = N(N-1)(N-2)/3! = ~ (N^3)/6 （组合数公式）
[-M, M]中随机 N 次，有 (2M+1)^N 种随机序列（每次随机都有 2M+1 种可能）
按照分步计数方法，将随机序列分为和为零的三元组和其余 N-3 个数
这些序列中，和为零的三元组有 3M^2 + 3M + 1 种可能。
其他不为零的 N-3 个位置有 (2M+1)^(N-3) 种可能。
总共有 ((N^3)/6) * (3M^2 + 3M + 1) * (2M+1)^(N-3) 种可能性
平均值为：
[((N^3)/6) * (3M^2 + 3M + 1) * (2M+1)^(N-3)] / (2M+1)^N
N^3/16M
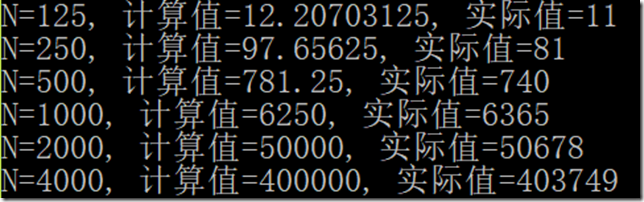
代码
using System; namespace _1._4._40
{
/*
* 1.4.40
*
* 随机输入下的 3-sum 问题。
* 猜测找出 N 个随机 int 值中和为 0 的整数三元组的数量所需的时间并验证你的猜想。
* 如果你擅长数学分析，请为此问题给出一个合适的数学模型，
* 其中所有值均匀的分布在 -M 和 M 之间，且 M 不能是一个小整数。
*
*/
class Program
{
// 数学模型
//
// N 个数可组成的三元组的总数为：
// C(N, 3) = N(N-1)(N-2)/3! = ~ (N^3)/6 （组合数公式）
// [-M, M]中随机 N 次，有 (2M+1)^N 种随机序列（每次随机都有 2M+1 种可能）
// 按照分步计数方法，将随机序列分为和为零的三元组和其余 N-3 个数
// 这些序列中，和为零的三元组有 3M^2 + 3M + 1 种可能。
// 其他不为零的 N-3 个位置有 (2M+1)^(N-3) 种可能。
// 总共有 ((N^3)/6) * (3M^2 + 3M + 1) * (2M+1)^(N-3) 种可能性
// 平均值为：
// [((N^3)/6) * (3M^2 + 3M + 1) * (2M+1)^(N-3)] / (2M+1)^N
// (N^3) * (3M^2 + 3M + 1) / 6 * (2M+1)^3
// ~ N^3 * 3M^2 / 6 * 8M^3
// N^3/16M
static void Main(string[] args)
{
int M = ; for (int n = ; n < ; n += n)
{
Random random = new Random();
int[] a = new int[n];
for (int i = ; i < n; ++i)
{
a[i] = random.Next( * M) - M;
}
Console.WriteLine($"N={n}, 计算值={Math.Pow(n, 3) / (16 * M)}, 实际值={ThreeSum.Count(a)}");
}
}
}
}
1.4.41
解答
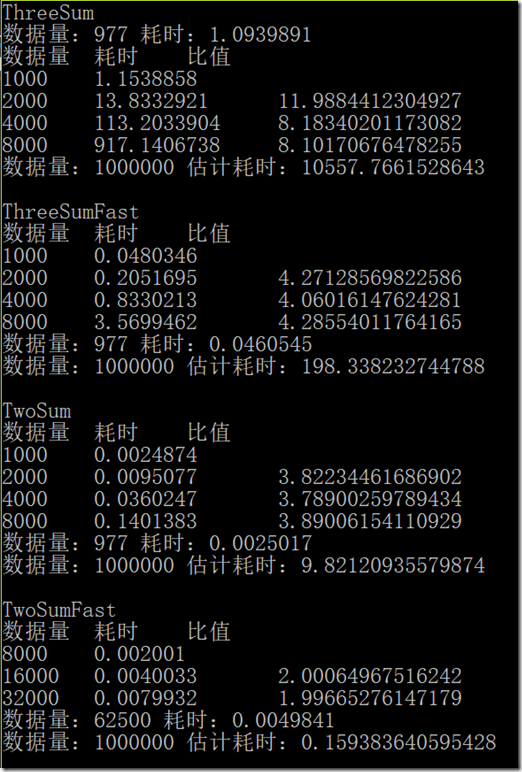
代码
这里使用了委托来简化代码。
DoublingRatio
using System;
using Measurement; namespace _1._4._41
{
public delegate int Count(int[] a);
static class DoublingRatio
{
/// <summary>
/// 从指定字符串中读入按行分割的整型数据。
/// </summary>
/// <param name="inputString">源字符串。</param>
/// <returns>读入的整型数组</returns>
private static int[] ReadAllInts(string inputString)
{
char[] split = new char[] { '\n' };
string[] input = inputString.Split(split, StringSplitOptions.RemoveEmptyEntries);
int[] a = new int[input.Length];
for (int i = ; i < a.Length; ++i)
{
a[i] = int.Parse(input[i]);
}
return a;
} /// <summary>
/// 使用给定的数组进行一次测试，返回耗时（毫秒）。
/// </summary>
/// <param name="Count">要测试的方法。</param>
/// <param name="a">测试用的数组。</param>
/// <returns>耗时（秒）。</returns>
public static double TimeTrial(Count Count, int[] a)
{
Stopwatch timer = new Stopwatch();
Count(a);
return timer.ElapsedTimeMillionSeconds();
} /// <summary>
/// 对 TwoSum、TwoSumFast、ThreeSum 或 ThreeSumFast 的 Count 方法做测试。
/// </summary>
/// <param name="Count">相应类的 Count 方法</param>
/// <returns>随着数据量倍增，方法耗时增加的比率。</returns>
public static double Test(Count Count)
{
double ratio = ;
double times = ; // 1K
int[] a = ReadAllInts(TestCase.Properties.Resources._1Kints);
double prevTime = TimeTrial(Count, a);
Console.WriteLine("数据量\t耗时\t比值");
Console.WriteLine($"1000\t{prevTime / 1000}\t"); // 2K
a = ReadAllInts(TestCase.Properties.Resources._2Kints);
double time = TimeTrial(Count, a);
Console.WriteLine($"2000\t{time / 1000}\t{time / prevTime}");
if (prevTime != )
{
ratio += time / prevTime;
}
else
{
times--;
}
prevTime = time; // 4K
a = ReadAllInts(TestCase.Properties.Resources._4Kints);
time = TimeTrial(Count, a);
Console.WriteLine($"4000\t{time / 1000}\t{time / prevTime}");
if (prevTime != )
{
ratio += time / prevTime;
}
else
{
times--;
}
prevTime = time; // 8K
a = ReadAllInts(TestCase.Properties.Resources._8Kints);
time = TimeTrial(Count, a);
Console.WriteLine($"8000\t{time / 1000}\t{time / prevTime}");
if (prevTime != )
{
ratio += time / prevTime;
}
else
{
times--;
}
prevTime = time; return ratio / times;
} public static double TestTwoSumFast(Count Count)
{
double ratio = ;
double times = ; // 8K
int[] a = ReadAllInts(TestCase.Properties.Resources._8Kints);
double prevTime = TimeTrial(Count, a);
Console.WriteLine("数据量\t耗时\t比值");
Console.WriteLine($"8000\t{prevTime / 1000}\t"); // 16K
a = ReadAllInts(TestCase.Properties.Resources._16Kints);
double time = TimeTrial(Count, a);
Console.WriteLine($"16000\t{time / 1000}\t{time / prevTime}");
if (prevTime != )
{
ratio += time / prevTime;
}
else
{
times--;
}
prevTime = time; // 32K
a = ReadAllInts(TestCase.Properties.Resources._32Kints);
time = TimeTrial(Count, a);
Console.WriteLine($"32000\t{time / 1000}\t{time / prevTime}");
if (prevTime != )
{
ratio += time / prevTime;
}
else
{
times--;
}
prevTime = time; return ratio / times;
}
}
}
主方法：
using System;
using Measurement; namespace _1._4._41
{
/*
* 1.4.41
*
* 运行时间。
* 使用 DoublingRatio 估计在你的计算机上用 TwoSumFast、TwoSum、ThreeSumFast 以及 ThreeSum 处理一个含有 100 万个整数的文件所需的时间。
*
*/
class Program
{
static void Main(string[] args)
{
int[] a = new int[];
Random random = new Random();
for (int i = ; i < ; ++i)
{
a[i] = random.Next() - ;
} // ThreeSum
Console.WriteLine("ThreeSum");
double time = DoublingRatio.TimeTrial(ThreeSum.Count, a);
Console.WriteLine($"数据量：977 耗时：{time / 1000}");
double doubleRatio = DoublingRatio.Test(ThreeSum.Count);
Console.WriteLine($"数据量：1000000 估计耗时：{time * doubleRatio * 1024 / 1000}");
Console.WriteLine(); //// ThreeSumFast
Console.WriteLine("ThreeSumFast");
time = DoublingRatio.TimeTrial(ThreeSumFast.Count, a);
doubleRatio = DoublingRatio.Test(ThreeSumFast.Count);
Console.WriteLine($"数据量：977 耗时：{time / 1000}");
Console.WriteLine($"数据量：1000000 估计耗时：{time * doubleRatio * 1024 / 1000}");
Console.WriteLine(); //// TwoSum
Console.WriteLine("TwoSum");
time = DoublingRatio.TimeTrial(TwoSum.Count, a);
doubleRatio = DoublingRatio.Test(TwoSum.Count);
Console.WriteLine($"数据量：977 耗时：{time / 1000}");
Console.WriteLine($"数据量：1000000 估计耗时：{time * doubleRatio * 1024 / 1000}");
Console.WriteLine(); // TwoSumFast
// 速度太快，加大数据量
a = new int[];
for (int i = ; i < ; ++i)
{
a[i] = random.Next() - ;
}
Console.WriteLine("TwoSumFast");
time = DoublingRatio.TimeTrial(TwoSumFast.Count, a);
doubleRatio = DoublingRatio.TestTwoSumFast(TwoSumFast.Count);
Console.WriteLine($"数据量：62500 耗时：{time / 1000}");
Console.WriteLine($"数据量：1000000 估计耗时：{time * doubleRatio * 16 / 1000}");
Console.WriteLine();
}
}
}
1.4.42
解答
这里我们把时限设置为一小时，使用上一题的数据估计。
1.ThreeSum 暴力方法在输入倍增时耗时增加 2^3 = 8 倍。
1K 数据耗费了 1.15 秒，在一小时内（3600 秒）可以完成 2^3 = 8K 数据。
2.ThreeSumFast 方法在输入倍增时耗时增加 2^2 = 4 倍。
1K 数据耗费了 0.05 秒，在一小时内（3600 秒）可以完成 2^8 = 256K 数据。
3.TwoSum 暴力方法在输入倍增时耗时增加 2^2 = 4 倍。
8K 数据耗费了 0.14 秒，在一小时内（3600 秒）可以完成 2^10 = 1024K 数据。
4.TwoSumFast 在输入倍增时耗时增加 2^1 = 2 倍。
32K 数据耗费了 0.008 秒，在一小时内（3600 秒）可以完成 2^16 = 65536K 数据。
1.4.43
解答
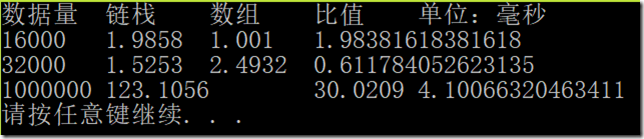
代码
修改后的 DoublingRatio
using System;
using Measurement; namespace _1._4._43
{
static class DoublingRatio
{
/// <summary>
/// 从指定字符串中读入按行分割的整型数据。
/// </summary>
/// <param name="inputString">源字符串。</param>
/// <returns>读入的整型数组</returns>
private static int[] ReadAllInts(string inputString)
{
char[] split = new char[] { '\n' };
string[] input = inputString.Split(split, StringSplitOptions.RemoveEmptyEntries); int[] a = new int[input.Length];
for (int i = ; i < a.Length; ++i)
{
a[i] = int.Parse(input[i]);
}
return a;
} /// <summary>
/// 使用给定的数组对链栈进行一次测试，返回耗时（毫秒）。
/// </summary>
/// <param name="a">测试用的数组。</param>
/// <returns>耗时（毫秒）。</returns>
public static double TimeTrialLinkedStack(int[] a)
{
LinkedStack<int> stack = new LinkedStack<int>();
int n = a.Length;
Stopwatch timer = new Stopwatch();
for (int i = ; i < n; ++i)
{
stack.Push(a[i]);
}
for (int i = ; i < n; ++i)
{
stack.Pop();
}
return timer.ElapsedTimeMillionSeconds();
} /// <summary>
/// 使用给定的数组对数组栈进行一次测试，返回耗时（毫秒）。
/// </summary>
/// <param name="a">测试用的数组。</param>
/// <returns>耗时（毫秒）。</returns>
public static double TimeTrialDoublingStack(int[] a)
{
DoublingStack<int> stack = new DoublingStack<int>();
int n = a.Length;
Stopwatch timer = new Stopwatch();
for (int i = ; i < n; ++i)
{
stack.Push(a[i]);
}
for (int i = ; i < n; ++i)
{
stack.Pop();
}
return timer.ElapsedTimeMillionSeconds();
} /// <summary>
/// 对链栈和基于大小可变的数组栈做测试。
/// </summary>
public static void Test()
{
double linkedTime = ;
double arrayTime = ;
Console.WriteLine("数据量\t链栈\t数组\t比值\t单位：毫秒");
// 16K
int[] a = ReadAllInts(TestCase.Properties.Resources._16Kints);
linkedTime = TimeTrialLinkedStack(a);
arrayTime = TimeTrialDoublingStack(a);
Console.WriteLine($"16000\t{linkedTime}\t{arrayTime}\t{linkedTime / arrayTime}"); // 32K
a = ReadAllInts(TestCase.Properties.Resources._32Kints);
linkedTime = TimeTrialLinkedStack(a);
arrayTime = TimeTrialDoublingStack(a);
Console.WriteLine($"32000\t{linkedTime}\t{arrayTime}\t{linkedTime / arrayTime}"); // 1M
a = ReadAllInts(TestCase.Properties.Resources._1Mints);
linkedTime = TimeTrialLinkedStack(a);
arrayTime = TimeTrialDoublingStack(a);
Console.WriteLine($"1000000\t{linkedTime}\t{arrayTime}\t{linkedTime / arrayTime}");
}
}
}
1.4.44
解答
每生成一个随机数都和之前生成过的随机数相比较。
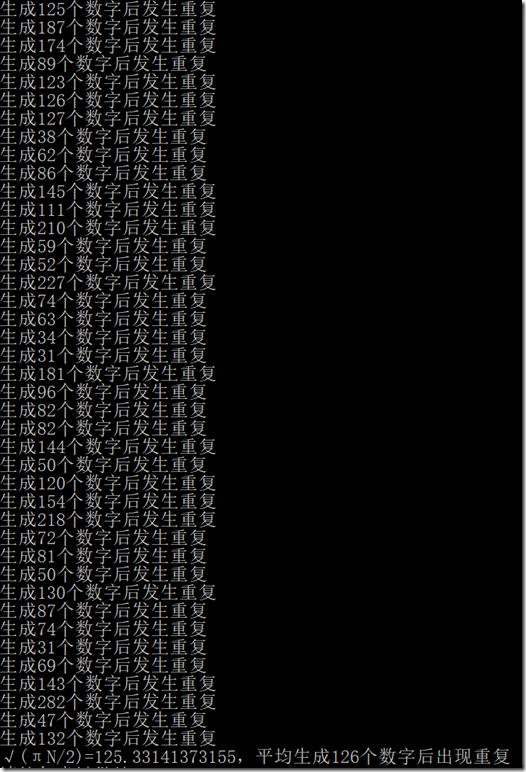
代码
using System; namespace _1._4._44
{
/*
* 1.4.44
*
* 生日问题。
* 编写一个程序，
* 从命令行接受一个整数 N 作为参数并使用 StdRandom.uniform() 生成一系列 0 到 N-1 之间的随机整数。
* 通过实验验证产生第一个重复的随机数之前生成的整数数量为 ~√(πN/2)。
*
*/
class Program
{
static void Main(string[] args)
{
Random random = new Random();
int N = ;
int[] a = new int[N];
int dupNum = ;
int times = ;
for (times = ; times < ; ++times)
{
for (int i = ; i < N; ++i)
{
a[i] = random.Next(N);
if (IsDuplicated(a, i))
{
dupNum += i;
Console.WriteLine($"生成{i + 1}个数字后发生重复");
break;
}
}
}
Console.WriteLine($"√(πN/2)={Math.Sqrt(Math.PI * N / 2.0)}，平均生成{dupNum / times}个数字后出现重复");
} /// <summary>
/// 检查是否有重复的数字出现。
/// </summary>
/// <param name="a">需要检查的数组。</param>
/// <param name="i">当前加入数组元素的下标。</param>
/// <returns>有重复则返回 true，否则返回 false。</returns>
static bool IsDuplicated(int[] a, int i)
{
for (int j = ; j < i; ++j)
{
if (a[j] == a[i])
{
return true;
}
}
return false;
} }
}
1.4.45
解答
建立一个布尔数组，将每次随机出来的数作为下标，将相应位置的布尔值改为 true，每次随机都检查一遍这个数组是否都是 true。
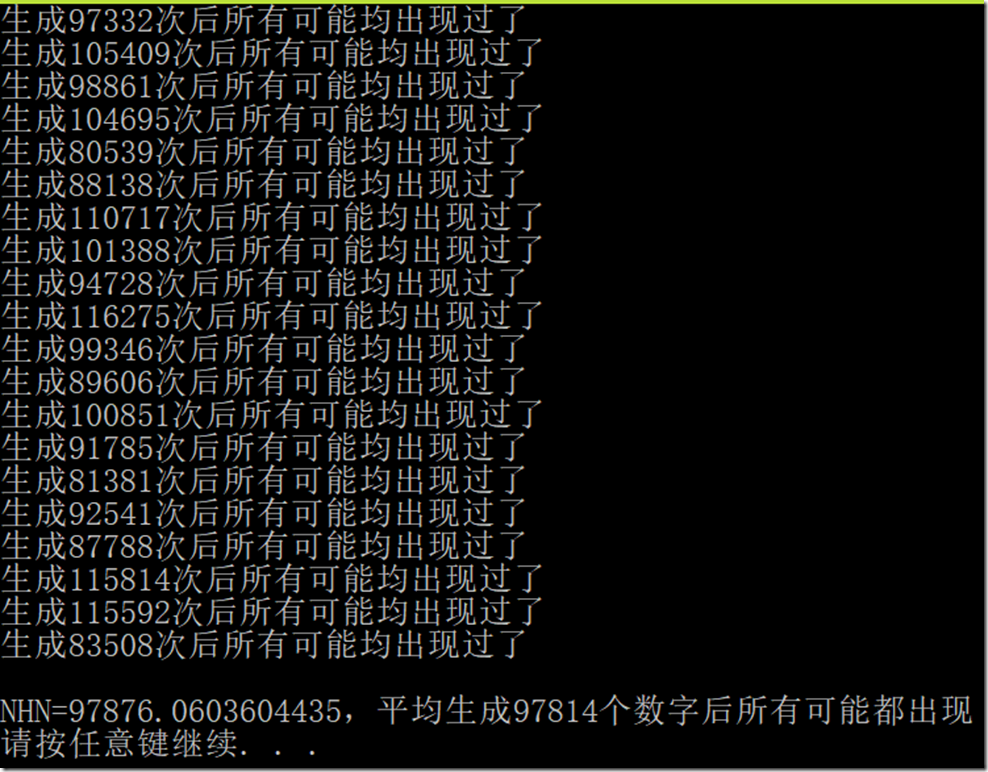
代码
using System; namespace _1._4._45
{
/*
* 1.4.45
*
* 优惠券收集问题。
* 用和上一题相同的方式生成随机整数。
* 通过实验验证生成所有可能的整数值所需生成的随机数总量为 ~NHN。
* （这里的 HN 中 N 是下标）
*
*/
class Program
{
// HN 指的是调和级数
static void Main(string[] args)
{
Random random = new Random();
int N = ;
bool[] a = new bool[N];
int randomSize = ;
int times = ;
for (times = ; times < ; ++times)
{
for (int i = ; i < N; ++i)
{
a[i] = false;
}
for(int i = ; true; ++i)
{
int now = random.Next(N);
a[now] = true;
if (IsAllGenerated(a))
{
randomSize += i;
Console.WriteLine($"生成{i}次后所有可能均出现过了");
break;
}
}
}
Console.WriteLine($"\nNHN={N * HarmonicSum(N)}，平均生成{randomSize / times}个数字后所有可能都出现");
} /// <summary>
/// 计算 N 阶调和级数的和。
/// </summary>
/// <param name="N">调和级数的 N 值</param>
/// <returns>N 阶调和级数的和。</returns>
static double HarmonicSum(int N)
{
double sum = ;
for (int i = ; i <= N; ++i)
{
sum += 1.0 / i;
}
return sum;
} /// <summary>
/// 检查所有数字是否都生成过了。
/// </summary>
/// <param name="a">布尔数组。</param>
/// <returns>全都生成则返回 true，否则返回 false。</returns>
static bool IsAllGenerated(bool[] a)
{
foreach (bool i in a)
{
if (!i)
return false;
}
return true;
}
}
}
算法（第四版）C# 习题题解——1.4的更多相关文章
- 算法（第四版）C#题解——2.1
算法(第四版)C#题解——2.1 写在前面 整个项目都托管在了 Github 上:https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csh ...
- 算法第四版 在Eclipse中调用Algs4库
首先下载Eclipse,我选择的是Eclipse IDE for Java Developers64位版本,下载下来之后解压缩到喜欢的位置然后双击Eclipse.exe启动 然后开始新建项目,File ...
- 算法第四版jar包下载地址
算法第四版jar包下载地址:https://algs4.cs.princeton.edu/code/
- 算法第四版-文字版-下载地址-Robert Sedgewick
下载地址:https://download.csdn.net/download/moshenglv/10777447 算法第四版,文字版,可复制,方便copy代码 目录: 第1章 基 础 ...... ...
- 二项分布。计算binomial(100,50,0.25)将会产生的递归调用次数（算法第四版1.1.27）
算法第四版35页问题1.1.27,估计用一下代码计算binomial(100,50,0.25)将会产生的递归调用次数: public static double binomial(int n,int ...
- 算法第四版学习笔记之优先队列--Priority Queues
软件:DrJava 参考书:算法(第四版) 章节:2.4优先队列(以下截图是算法配套视频所讲内容截图) 1:API 与初级实现 2:堆得定义 3:堆排序 4:事件驱动的仿真 优先队列最重要的操作就是删 ...
- 算法第四版学习笔记之快速排序 QuickSort
软件:DrJava 参考书:算法(第四版) 章节:2.3快速排序(以下截图是算法配套视频所讲内容截图) 1:快速排序 2:
- C程序设计(第四版)课后习题完整版 谭浩强编著
//复习过程中,纯手打,持续更新,觉得好就点个赞吧. 第一章:程序设计和C语言 习题 1.什么是程序?什么是程序设计? 答:程序就是一组计算机能识别和执行的指令.程序设计是指从确定任务到得到结果,写出 ...
- 算法第四版 coursera公开课 普林斯顿算法 ⅠⅡ部分 Robert Sedgewick主讲《Algorithms》
这是我在网上找到的资源,下载之后上传到我的百度网盘了. 包含两部分:1:算法视频的种子 2:字幕 下载之后,请用迅雷播放器打开,因为迅雷可以直接在线搜索字幕. 如果以下链接失效,请在下边留言,我再更新 ...
- 相似度分析，循环读入文件(加入了HanLP,算法第四版的库)
相似度分析的,其中的分词可以采用HanLP即可: http://www.open-open.com/lib/view/open1421978002609.htm /****************** ...
随机推荐
- Spring Security Session并发控制原理解析
当使用spring security 的标签,如下,其中<sec:session-management>对应的SessionManagementFilter.从名字可以看出,这是一个管理S ...
- Express全系列教程之(一)：Express的安装 和第一个程序
前言 ndoe.js,一个基于javsscript运行环境的服务器语言,它的出现使得javascript有能力去实现服务器操作.在gitHub上ndoe.js的star数已接近6万,可见其受欢迎程度: ...
- net-tools与iproute2
net-tools与iproute2 我们知道redhat系列发行版7x版本中最小化安装是没有net-tools工具包的,默认使用iproute2工具包,最直观的感受是ifconfig命令被ip命令所 ...
- Spark入门到精通--（外传）Cloudera CDH5.5.4搭建
http://www.mamicode.com/info-detail-601202.html continue...
- Spark入门到精通--（第十节）环境搭建（ZooKeeper和kafka搭建）
上一节搭建完了Hive,这一节我们来搭建ZooKeeper,主要是后面的kafka需要运行在上面. ZooKeeper下载和安装 下载ZooKeeper 3.4.5软件包,可以在百度网盘进行下载.链接 ...
- win7 64位系统下安装autoitlibrary库遇到问题解决
转载来自http://blog.sina.com.cn/s/blog_53f023270101skyq.html 今天需要在win7 64位系统下安装autoitlibrary库,起初安装好了robo ...
- numpy交换列
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(x) x = x[:, [1, 0, 2]] print(x) 输出 [[1 2 3] [4 ...
- pc端字体大小自适应几种方法
$(window).resize(function ()// 绑定到窗口的这个事件中 { var whdef = 100/1920;// 表示1920的设计图,使用100PX的默认值 var wH ...
- 【Linux】-NO.160.Linux.1 -【升级Centos7】
Style:Mac Series:Java Since:2018-09-10 End:2018-09-10 Total Hours:1 Degree Of Diffculty:5 Degree Of ...
- GIT回滚master分支到指定tag版本
master版本上线以后一般要打一个tag备份,以防事态有变,这是一个好习惯,如果以后有问题也可以放心的回滚版本,那么怎么用tag版本覆盖mastaer呢,其实只有几个命令 1.查看分支 git br ...