POJ 1149 PIGS 【最大流】

<题目链接>

题目大意：
有一个养猪场，厂长没有钥匙，这个养猪场一共M个猪圈，N个顾客，每个顾客有一些猪圈的钥匙，每个顾客需要一些猪，问你厂长最多能卖多少猪？这里有个条件是，厂长可以在一个顾客买完后，调整没有锁门的猪圈中猪数量，比如，把几个猪圈中的猪全部转到一个猪圈内（这个条件会影响到后期建图），然后再关门，等下一个顾客。

解题分析：

首先根据题意，将这个问题抽象成一个朴素的模型，

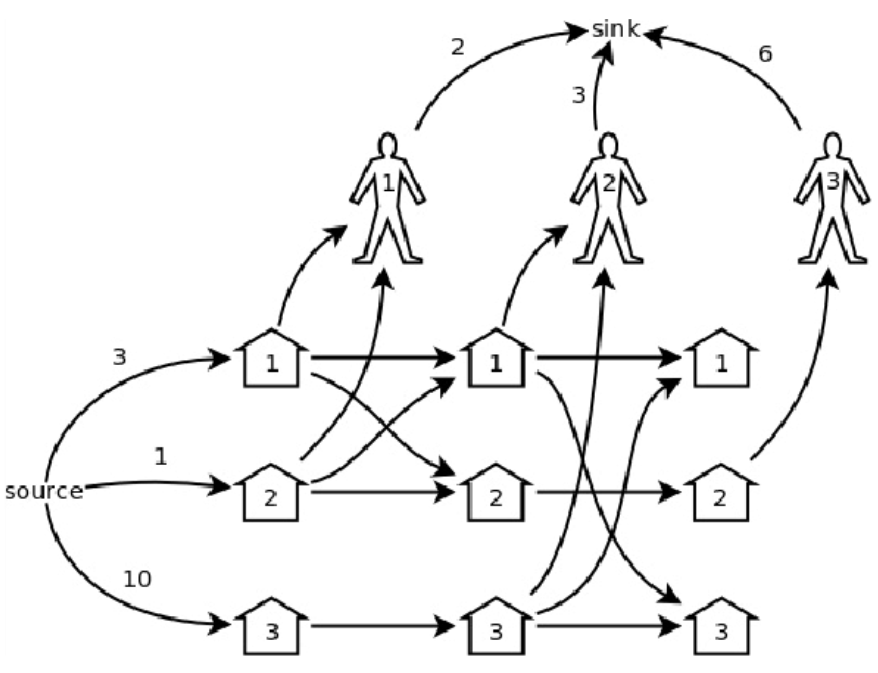
因为这样建图，图中最多可能有$2+N+M+N*M (≈1e5)$个节点。在这样的图上跑网络流速度会很慢，我们可以通过合并一些等效的点来达到简化模型的目的。

规律 1.  如果几个结点的流量的来源完全相同，则可以把它们合并成一个。

规律 2.  如果几个结点的流量的去向完全相同，则可以把它们合并成一个。

规律 3.  如果从点 u 到点 v 有一条容量为∞的边，并且点 v 除了点 u 以外没有别的流量来源，则可以把这两个结点合并成一个。

具体简化过程见  >>>

简化后的图为：

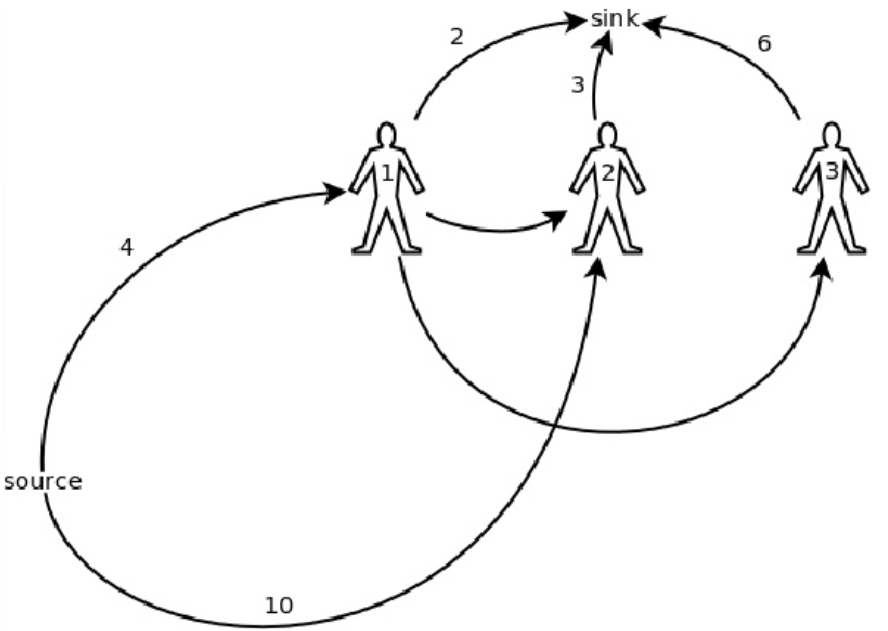
因此，最终的建图方案就是：源点到所有第一个打开各个猪圈的人连上一条边，容量为这个猪圈的数量上限，然后，上一个打开这个猪圈的人向下一个打开这个猪圈的人连一条容量为无穷的边，最后，所有人向汇点连一条边，容量为他所能拿的猪数量的上限。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;

typedef long long ll;
const ll INF = 1e18;
const int N = 1e3+;

template<typename T>
inline void read(T&x){
    x=;int f=;char ch=getchar();
    while(ch<''||ch>''){ if(ch=='-')f=-;ch=getchar(); }
    while(ch>=''&&ch<=''){ x=x*+ch-'';ch=getchar(); }
    x*=f;
}
struct Dinic
{
    struct edge{ int from,to;ll cap,flow; };
    vector<edge>es;
    vector<int>G[N];
    bool vis[N];
    int dist[N],iter[N];
    void init(int n){
        for(int i=; i<=n+; i++)G[i].clear();
        es.clear();
    }
    void addedge(int from,int to,ll cap){
        es.push_back((edge){from,to,cap,});    //将边存储的边表
        es.push_back((edge){to,from,,});
        int x=es.size();
        G[from].push_back(x-);    //G[u][i]记录以u为顶点的第i条边的反边在es中的编号
        G[to].push_back(x-);
    }
    bool BFS(int s,int t){      //bfs将该图划分成分层图
        memset(vis,,sizeof(vis));
        queue <int> q;
        vis[s]=;
        dist[s]=;
        q.push(s);
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int i=; i<G[u].size(); i++){
                edge &e=es[G[u][i]];
                if(!vis[e.to]&&e.cap>e.flow){
                    vis[e.to]=;
                    dist[e.to]=dist[u]+;
                    q.push(e.to);
                }
            }
        }
        return vis[t];
    }
    int DFS(int u,int t,ll f){
        if(u==t||f==)return f;
        int lastflow=,d;
        for(int &i=iter[u]; i<G[u].size(); i++){
            edge &e=es[G[u][i]];
            if(dist[u]+==dist[e.to]&&(d=DFS(e.to,t,min(f,e.cap-e.flow)))>){
                e.flow+=d;     //正边真实流量-d
                es[G[u][i]^].flow-=d;  //反边真实流量+d
                lastflow+=d;    //得到现在搜得的能够流入汇点的流量
                f-=d;      //找到一条增广路之后，减去这条路的流量，然后继续从这个顶点的其它边开始寻找增广路
                if(f==)break;
            }
        }
        return lastflow;
    }
    int Maxflow(int s,int t){
        int flow=;
        while(BFS(s,t)){
            memset(iter,,sizeof(iter));
            int d=;
            while(d=DFS(s,t,INF))flow+=d;
        }
        return flow;
    }
}dinic;

int n,m,st,ed,last[N],pig[N];    //last记录上一个打开对应猪圈的人
int main(){
    read(m);read(n);st=;ed=n+;
    for(int i=;i<=m;i++) read(pig[i]);
    for(int i=;i<=n;i++){
        int k;read(k);
        while(k--){
            int x;read(x);
            if(!last[x]) dinic.addedge(st,i,pig[x]),last[x]=i;     //如果是第一个打开该猪圈的人，就直接从源点向他连一条边
            else dinic.addedge(last[x],i,INF),last[x]=i;      //如果这个猪圈已经被打开过了，就从上一个打开的人向他连一条边
        }
        ll cal;read(cal);
        dinic.addedge(i,ed,cal);      //每个人向汇点连一条边，容量为他们能够拿的猪的上限
    }
    cout<<dinic.Maxflow(st,ed)<<endl;
}