[APIO2010]

A.特别行动队

n<=1000000

看了数据范围和题目感觉就像是斜率优化，然后瞎推了一波式子，没想到A了。

sij表示i+1到j的权值和。

j比k优秀  $$fj+a*sij^{2}+b*sij+c>fk+a*sik^{2}+b*sik+c$$

然后乱整理$$2*a*si<\frac{fj-fk}{sj-sk}+a*(sj+sk)-b$$

si递增，维护上凸。

#include<iostream>
#include<cstdio>
#define ll long long
#define ld long double
#define MN 1000000
using namespace std;
inline int read()
{
    int x =  , f = ; char ch = getchar();
    while(ch < '' || ch > ''){ if(ch == '-') f = -;  ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return x * f;
}

ll f[MN+],s[MN+],a,b,c;
int top=,tail=,q[MN+];
int n;

ll calc(ll x){return a*x*x+b*x+c;}

ld solve(int x,int y)
{
    return (ld)(f[x]-f[y])/(s[x]-s[y])+(ld)a*(s[x]+s[y])-(ld)b;
}

void ins(int x)
{
    while(top>tail&&solve(x,q[top])>solve(q[top],q[top-])) top--;
    q[++top]=x;
}

int get(ll x)
{
    while(top>tail&&solve(q[tail+],q[tail])>x) tail++;
    return q[tail];
}

int main()
{
    n=read();a=read();b=read();c=read();
    for(int i=;i<=n;i++) s[i]=s[i-]+read();
    for(int i=;i<=n;i++)
    {
        int from=get(1LL**a*s[i]);
        f[i]=f[from]+calc(s[i]-s[from]);
        ins(i);
    }
    cout<<f[n];
    return ;
}

B.巡逻

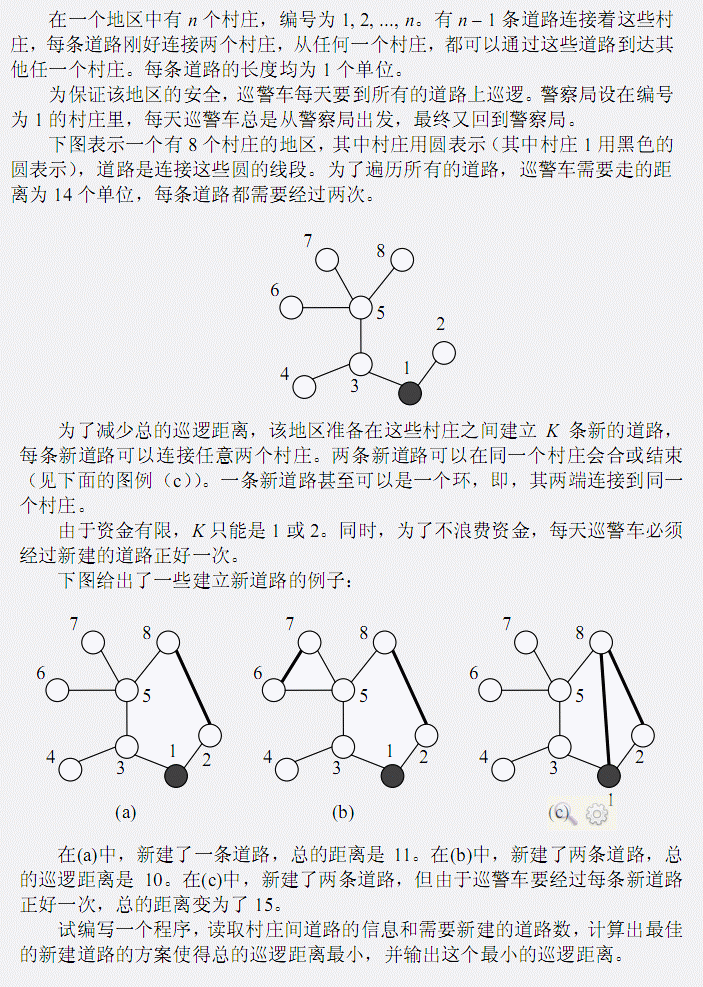
n<=100000

题解：yy一下可以发现，k=1找的是最长链，答案是(n-1)*2+1-长度

k=2的时候，我们把最长链上的边改成-1，然后再跑最长链就行啦。答案是(n-1)*2+2-长度之和。

我一开始yy了很牛逼的树形dp，然后写了半天还是有一个点过不了。。。百度一下题解，真的妙

#include<iostream>
#include<cstdio>
#define MN 100000
using namespace std;
inline int read()
{
    int x =  , f = ; char ch = getchar();
    while(ch < '' || ch > ''){ if(ch == '-') f = -;  ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return x * f;
}

struct edge{int to,next,w;}e[MN*+];
int head[MN+],cnt=,n;
int f[MN+],w1[MN+],f1[MN+],mx[MN+],mx2[MN+],ans=,K,from; 

void solve(int x,int fa)
{
    int from1=,from2=;mx[x]=mx2[x]=f[x]=;
    for(int i=head[x];i;i=e[i].next)
    if(e[i].to!=fa)
    {
        solve(e[i].to,x);
        if(f[e[i].to]+e[i].w>mx[x]) mx2[x]=mx[x],mx[x]=f[e[i].to]+e[i].w,from2=from1,from1=e[i].to;
        else if(f[e[i].to]+e[i].w>mx2[x]) mx2[x]=f[e[i].to]+e[i].w,from2=e[i].to;
    }
    if(mx[x]+mx2[x]>ans) ans=mx[x]+mx2[x],from=x;
    f[x]=mx[x];mx[x]=from1;mx2[x]=from2;
}

void relabel(int x)
{
    for(int i=head[x];i;i=e[i].next)
        if(e[i].to==mx[x])
            e[i].w=-,relabel(e[i].to);
}

void ins(int f,int t)
{
    e[++cnt]=(edge){t,head[f],};head[f]=cnt;
    e[++cnt]=(edge){f,head[t],};head[t]=cnt;
}

int main()
{
    n=read();K=read();
    for(int i=;i<n;i++) ins(read(),read());
    solve(,);if(K==)return *printf("%d",*n--ans);
    n=n*-ans;ans=;
    for(int i=head[from];i;i=e[i].next)
        if(e[i].to==mx[from]||e[i].to==mx2[from])
            e[i].w=-,relabel(e[i].to);
    solve(,);
    printf("%d\n",n-ans);
    return ;
}

3.signaling  信号覆盖

题意：给定平面上n个点，满足没有三个点共线，没有四个点共圆。你现在随意选出三个点，求这三个点的外接圆内包含的点的期望个数。  $n\leqslant 1500$

题解：对于每一个三个点包含一个点的情况，我们都能抽象成一个四边形。我们发现凸四边形有两种方法盖住四个点，而凹多边形只有一种方法，所以凸多边形的贡献是2，凹的是1，他们的个数相加是C(n,4),所以我们只要计算凸多边形或者凹多边形的个数就行了。我们枚举凹多边形的凹点，然后按照极角排序，然后枚举一个点，找出最远的点使得他们之间的夹角不超过平角，通过组合算出个数，最后除以总的方案数C(n,3) 。

复杂度$n^{2}logn$

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define MN 1500
#define ll long long
using namespace std;
inline int read()
{
    int x =  , f = ; char ch = getchar();
    while(ch < '' || ch > ''){ if(ch == '-') f = -;  ch = getchar();}
    while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
    return x * f;
}

struct P
{
    double x,y,alpha;
    void getAlpha(double xx,double yy){alpha=atan2(x-xx,y-yy);}
    friend double cross(P a,P b){return a.x*b.y-a.y*b.x;}
    bool operator == (P b){return x==b.x&&y==b.y;}
    bool operator < (const P &b) const {return alpha<b.alpha;}
    P operator - (P b){return (P){x-b.x,y-b.y};}
    void print()
    {
        cout<<x<<" "<<y<<" "<<alpha<<endl;
    }
}p[MN+],pt[MN+];

int n,top;
double ans=;

ll work(P th)
{
    ll sum=1LL*(n-)*(n-)*(n-)/;int num=;top=;
    for(int i=;i<n;i++,--num)
    {
        while(cross(p[i]-th,p[top]-th) <= )
        {
            top=top%(n-)+,num++;
            if(top==i) break;
        }
        sum-=1LL*(num)*(num-)/;
    }
    return sum;
}

int main()
{
    n=read();if(n==) return *puts("");
    for(int i=;i<=n;i++) pt[i].x=p[i].x=read(),pt[i].y=p[i].y=read();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<n;j++)
        {
            if(pt[i]==p[j]) swap(p[j],p[n]);
            p[j].getAlpha(pt[i].x,pt[i].y);
        }
        sort(p+,p+n);
        ans+=work(pt[i]);
    }
    double A=1LL*n*(n-)*(n-)/,B=1LL*n*(n-)*(n-)*(n-)/;
    printf("%.6lf\n",(ans+*(B-ans))/A+);
    return ;
}