【机器学习】--GBDT算法从初始到应用

一、前述

提升是一种机器学习技术，可以用于回归和分类的问题，它每一步产生弱预测模型(如决策树)，并加权累加到总模型中；如果每一步的弱预测模型的生成都是依据损失函数的梯度方式的，那么就称为梯度提升(Gradient boosting)提升技术的意义：如果一个问题存在弱预测模型，那么可以通过提升技术的办法得到一个强预测模型。

二、算法过程

给定输入向量X和输出变量Y组成的若干训练样本(X 1 ,Y 1 ),(X 2 ,Y 2 )......(X n ,Y n )，

目标是找到近似函数F(X)，使得损失函数L(Y,F(X))的损失值最小。

L损失函数一般采用最小二乘损失函数或者绝对值损失函数

最优解为：

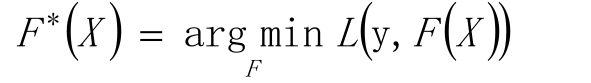
假定F(X)是一族最优基函数f i (X)的加权和：

以贪心算法的思想扩展得到Fm(X)，求解最优f

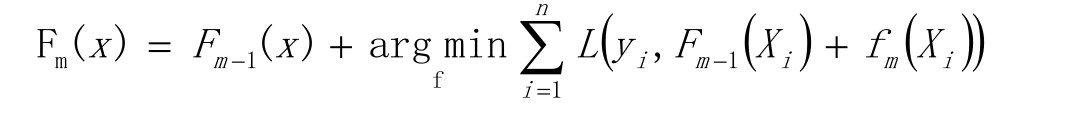
以贪心法在每次选择最优基函数f时仍然困难，使用梯度下降的方法近似计算

给定常数函数F 0 (X)

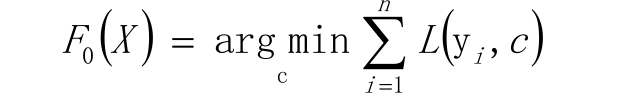
计算残差

使用数据 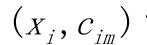计算拟合残差的基函数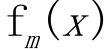

 计算步长

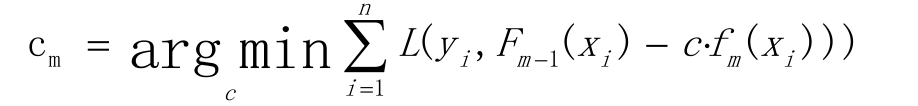
更新模型(梯度的思想)

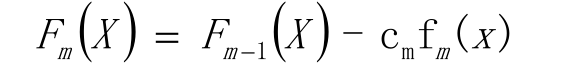
三、GDBT算法思想

GBDT由三部分构成：DT(Regression Decistion Tree)、GB(Gradient Boosting)和Shrinkage，由多棵决策树组成，所有树的结果累加起来就是最终结果
迭代决策树和随机森林的区别：
随机森林使用抽取不同的样本构建不同的子树，也就是说第m棵树的构建和前m-1棵树的结果是没有关系的
迭代决策树在构建子树的时候，使用之前子树构建结果后形成的残差作为输入数据构建下一个子树；然后最终预测的时候按照子树构建的顺序进行预测，并将预测结果相加