JavaScript的数据结构和算法
所有JavaScript对象都有hasOwnProperty(value)的方法,用来返回一个表明对象是不是具有这个value Key值属性的布尔值。
javaScript的方法 具有delete的方法 事实上在业务中很少去删除真实的数据,但是在做一下添加和删除时 为了配合后端 也是会用到的。
在javaScript中我们通常使用数据结构是对象和数组, 更常用的是链表结构,添加和删除方便,不需要去遍历。这是一个很节省性能的事情。
new.target 是一个新增的管理 实例函数的方法 如果这个函数被new 或者继承调用 那么就会被返回当前的class或者function 否则返回一个undefined 需要些在constructor里。
set类 在JavaScript中体现为集合的形式 类似对象不同于对象只能一组一组的保存,是可以多组进行保存的类比其他的语言set类 它算是比较完善的了,set类的结构 类似{1:1,2:2} 以key:value的形式保存起来。 我们可以使用它用来求交集,并集,差集,子集等等 类似于对象所以我们可以使用delete 来它其中的某一项,获取它的长度可以通过 用Object.keys来枚举它拿到这个数组的length。添加可以使用其自己本省所带的add的方法。检测是否有这个属性key 我们可以使用hasOwnProperty()的方法来确认这个属性。 这里的集合存储的是一组互不相同的元素.(也就是说这里不适用多重集)。
散列表和字典结构 在JavaScript中体现为Map类。顾名思义 主要是为了做映射使用。用来存储唯一的值,结构也是使用key: value的形式。
非顺序数据结构有散列法和树。
一个树的结构包含一系列的父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点。
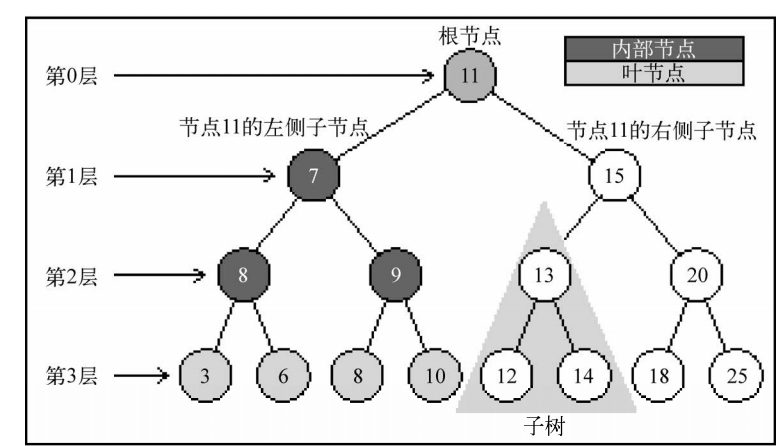
(这里图的第二层8是错误的 应该是5)
位于树顶部的节点叫做根节点。它没有父节点。树种的每个元素都叫做节点。节点分为内部节点和外部节点。 至少有一个字节点的节点称为内部节点(7,5,9,15,13,20是内部节点).没有子元素的节点称为外部节点或叶节点(3,6,8,10,12,14,18,25都是叶节点)。
一个节点可以有祖先和后代。一个节点(除了根节点)的祖先包括父节点,祖父节点,曾祖父节点等等一个节点的后代包括它下面的所有节点。如图上节点9的祖先节点有7和11,而他的字节点有8和10.
有关于树的另一个术语是子树。子树由节点和它的后代构成。比如节点13和12,14构成了图中的子树。
节点的一个属性是深度,节点的深度取决于它的祖先节点的数量。比如,节点10有3个祖先节点(9,7,11),那么它的深度就是3.
树的高度取决于所有节点深度的最大值。一棵树也可以被分解成层级。根节点在第0层,它的字节点在第一层。
二叉树和二叉搜索树
二叉树的节点最多只能有两个子节点:一个是左侧子节点,另一个是右侧的子节点。这些定义有助于我们写出更高效的向/从树中插入,查找和删除节点的算法。
上图就是一个二叉搜索树(BST)。属于二叉树的一种。
如何用代码去申明一个二叉搜索树。
首先定义一个function BinarySearchTree类。
首先: 我们先明确二叉搜索树.
class BinarySearchTree {
consturtor() {
this.Node = class {
consturtor(key){
this.key = key; //这是我们的节点值 变量私有化
this.left = null ; // 根节点起始左位置的初始化
this.right = null; // 根节点起始右位置的初始化
}
}
this.root = null ; //起始的根节点
}
}
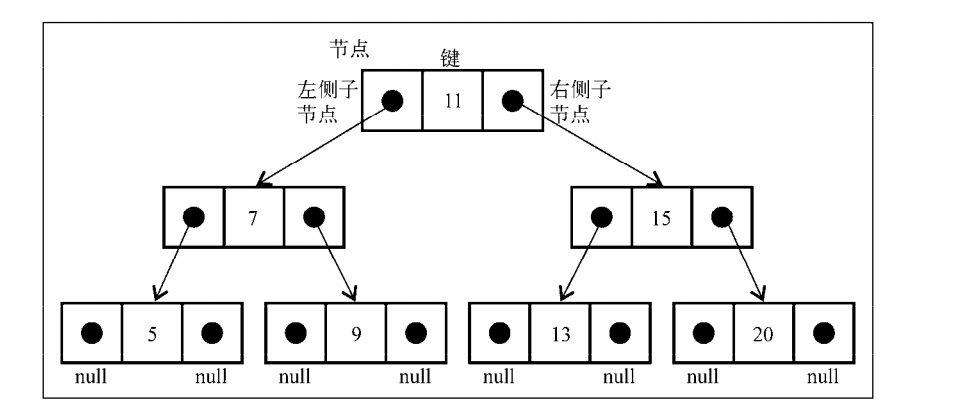
和链表一样,都是通过指针来表示节点之间的关系(术语称为边)。在双向链表中,每个节点都包含两个指针,一个指向下一个节点,一个指向上一个节点。对于树,使用同样的方式(也使用两个指针)
class BinarySearchTree {
constructor() {
this.Node = class {
constructor(key){
this.key = key; //这是我们的节点值 变量私有化
this.left = null ; // 根节点起始左位置的初始化
this.right = null; // 根节点起始右位置的初始化
}
}
this.root = null ; //起始的根节点
}
insert(key) {
const newNode = new this.Node(key);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
insertNode(node, newNode) { // 尾递归查询节点
if (newNode.key < node.key) { //如果新的节点值小于父节点的值
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
}
const BinarySearchTree1 = new BinarySearchTree();
BinarySearchTree1.insert(11);
BinarySearchTree1.insert(7);
BinarySearchTree1.insert(15);
BinarySearchTree1.insert(5);
BinarySearchTree1.insert(3);
BinarySearchTree1.insert(9);
BinarySearchTree1.insert(8);
BinarySearchTree1.insert(10);
BinarySearchTree1.insert(13);
BinarySearchTree1.insert(12);
BinarySearchTree1.insert(14);
BinarySearchTree1.insert(20);
BinarySearchTree1.insert(18);
BinarySearchTree1.insert(25);
console.log(BinarySearchTree1);
这样我们就实现了 插入的方法。
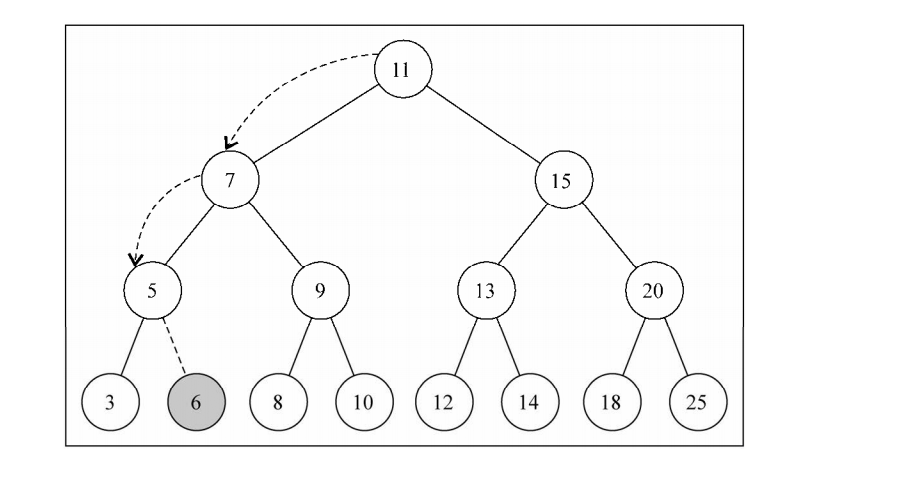
这就是我们得到的二叉树。
树的遍历分为三种 中序遍历 先序遍历 后序遍历
中序遍历是一种以上行顺序的访问的BST所有节点的遍历方式,也就是以从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。
class BinarySearchTree {
constructor() {
this.Node = class {
constructor(key){
this.key = key; //这是我们的节点值 变量私有化
this.left = null ; // 节点起始左位置的初始化
this.right = null; // 节点起始右位置的初始化
}
}
this.root = null ; //起始的根节点
}
insert(key) {
const newNode = new this.Node(key);
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
}
insertNode(node, newNode) {
if (newNode.key < node.key) { //如果新的节点值小于父节点的值
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
}
inOrderTraverseNode(node, callback) {
if (node !== null) { //{2}
this.inOrderTraverseNode(node.left, callback); //{3}
callback(node.key); //{4}
this.inOrderTraverseNode(node.right, callback); //{5}
}
}
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback);
}
printNode(value) {
console.log(value);
}
}
const BinarySearchTree1 = new BinarySearchTree();
BinarySearchTree1.insert(11);
BinarySearchTree1.insert(7);
BinarySearchTree1.insert(15);
BinarySearchTree1.insert(5);
BinarySearchTree1.insert(3);
BinarySearchTree1.insert(9);
BinarySearchTree1.insert(8);
BinarySearchTree1.insert(10);
BinarySearchTree1.insert(13);
BinarySearchTree1.insert(12);
BinarySearchTree1.insert(14);
BinarySearchTree1.insert(20);
BinarySearchTree1.insert(18);
BinarySearchTree1.insert(25);
BinarySearchTree1.inOrderTraverse(BinarySearchTree1.printNode);
console.log(BinarySearchTree1);
搜索树中的值
在树中, 有三种经常执行的搜索类型:
最小值;
最大值;
搜索特定的值。
搜索最小值和最大值
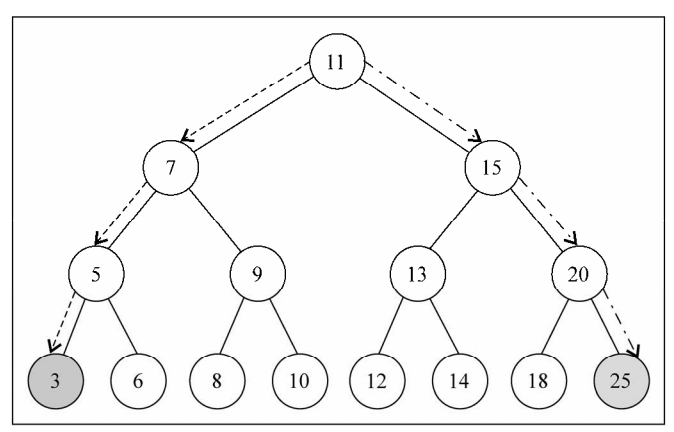
JavaScript的数据结构和算法的更多相关文章
- javascript实现数据结构与算法系列:栈 -- 顺序存储表示和链式表示及示例
栈(Stack)是限定仅在表尾进行插入或删除操作的线性表.表尾为栈顶(top),表头为栈底(bottom),不含元素的空表为空栈. 栈又称为后进先出(last in first out)的线性表. 堆 ...
- JavaScript 版数据结构与算法(二)队列
今天,我们要讲的是数据结构与算法中的队列. 队列简介 队列是什么?队列是一种先进先出(FIFO)的数据结构.队列有什么用呢?队列通常用来描述算法或生活中的一些先进先出的场景,比如: 在图的广度优先遍历 ...
- 第一章:javascript: 数据结构与算法
在前端工程师中,常常有一种声音,我们为什么要学数据结构与算法,没有数据结构与算法,我们一样很好的完成工作.实际上,算法是一个宽泛的概念,我们写的任何程序都可以称为算法,甚至往冰箱里放大象,也要通过开门 ...
- JavaScript 版数据结构与算法(一)栈
今天,我们要讲的是数据结构与算法中的栈. 栈的简介 栈是什么?栈是一个后进先出(LIFO)的数据结构.栈有啥作用?栈可以模拟算法或生活中的一些后进先出的场景,比如: 十进制转二进制,你需要将余数倒序输 ...
- JavaScript 版数据结构与算法(三)链表
今天,我们要讲的是数据结构与算法中的链表. 链表简介 链表是什么?链表是一种动态的数据结构,这意味着我们可以任意增删元素,它会按需扩容.为何要使用链表?下面列举一些链表的用途: 因为数组的存储有缺陷: ...
- JavaScript 版数据结构与算法(四)集合
今天,我们要讲的是数据结构与算法中的集合. 集合简介 什么是集合?与栈.队列.链表这些顺序数据结构不同,集合是一种无序且唯一的数据结构.集合有什么用?在 Python 中,我经常使用集合来给数组去重: ...
- javascript实现数据结构与算法系列:循环链表与双向链表
循环链表(circular linked list) 是另一种形式的链式存储结构.它的特点是表中最后一个结点的指针域指向头结点,整个表形成一个环. 循环链表的操作和线性链表基本一致,仅有细微差别. w ...
- javascript实现数据结构与算法系列
1.线性表(Linear list) 线性表--简单示例及线性表的顺序表示和实现 线性表--线性链表(链式存储结构) 线性表的静态单链表存储结构 循环链表与双向链表 功能完整的线性链表 线性链表的例子 ...
- JavaScript 的数据结构与算法
1数组 1.1方法列表 数组的常用方法如下: concat: 链接两个或者更多数据,并返回结果. every: 对数组中的每一项运行给定的函数,如果该函数对每一项都返回true,则返回true. fi ...
随机推荐
- 1.6W star 的 JCSprout 阅读体验大提升
万万没想到 JCSprout 截止目前居然有将近1.6W star.真的非常感谢各位大佬的支持. 年初时创建这个 repo 原本只是想根据自己面试与被面试的经历记录一些核心知识点,结果却是越写越多. ...
- java~日期与字符串的转化
在Java里我们可以通过SimpleDateFormat实现日期类型的格式化,即将它转为指定格式的字符串,当然像YearMonth这种特殊的类型,实现字符串转化最为容易,即直接toString()即可 ...
- Java进阶篇设计模式之三 ----- 建造者模式和原型模式
前言 在上一篇中我们学习了工厂模式,介绍了简单工厂模式.工厂方法和抽象工厂模式.本篇则介绍设计模式中属于创建型模式的建造者模式和原型模式. 建造者模式 简介 建造者模式是属于创建型模式.建造者模式使用 ...
- 学习ASP.NET Core Razor 编程系列十三——文件上传功能(一)
学习ASP.NET Core Razor 编程系列目录 学习ASP.NET Core Razor 编程系列一 学习ASP.NET Core Razor 编程系列二——添加一个实体 学习ASP.NET ...
- SQL优化 MySQL版 -分析explain SQL执行计划与Type级别详解
type索引类型.类型 作者 : Stanley 罗昊 [转载请注明出处和署名,谢谢!] 注:看此文章前,需要有一定的Mysql基础或观看上一篇文章,该文章传送门: https://www.cnblo ...
- centos7 python3 pip
pip of python3 installed is play well with Django and spider. #安装pip可以很好的使用django和爬虫 wget https:// ...
- RDIFramework.NET V3.3 WinForm版新增订单管理主从表事例
功能描述 无论什么系统,除了常规的单表处理外,主从表的应用都是非常普遍的,RDIFramework.NET V3.3 WinForm版本中新增了一个主从表的事例供大家参考.主从表的界面设计大同小异,主 ...
- 如何使用.net开发一款小而美的O2O移动应用? ——“家庭小秘”APP介绍及采访记录
“家庭小秘”是一款“互联网+生活服务”平台,为市民家庭提供优质家庭生活服务和企业后勤服务,包含了用户注册.购买预约.订单查询.充值付款.即时通讯等功能. 这款应用已上线至AppStore和安卓的应用商 ...
- 【1】Asp.Net Core2.2从环境配置到应用建立
作者:Eleven 来源:公众号[软谋net] [前言] .Net Core开源&跨平台,已经肉眼可见将成为.Net平台的未来,在企业招聘需求上已经频频见到,接触到很多公司内部都已经开始尝试C ...
- 从零讲解搭建一个NIO消息服务端
本文首发于本博客,如需转载,请申明出处. 假设 假设你已经了解并实现过了一些OIO消息服务端,并对异步消息服务端更有兴趣,那么本文或许能带你更好的入门,并了解JDK部分源码的关系流程,正如题目所说,笔 ...
