BFS-九宫格重排(详解)
BFS将近两年没练过题了,今天重新回忆下以前刷的蓝桥杯题:九宫格重排
样例输入
//初始状态
//终点状态
样例输出
//最短步数
样例输入
//初始状态
//终点状态
样例输出
//最短步数
思路
以下图为例,空格0可以走上下左右4步 :
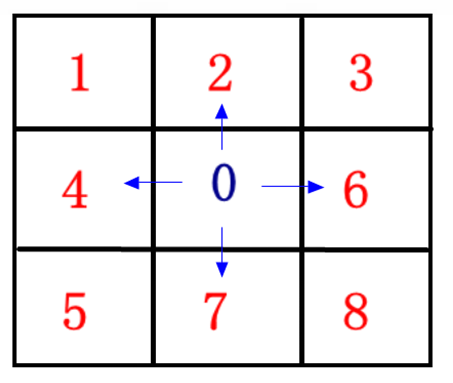
当前0位于的位置是(1,1),所以可以移动到(1-1,1),(1,1+1),(1+1,1),(1,1-1)
然后通过康拓展开来校验,移动的位置是否走过,是否已到终点,是否越界。
康拓展开
表示的是当前排列在n个不同元素的全排列中的名次.
公式为:
X=a[n]*(n-)!+a[n-]*(n-)!+...+a[i]*(i-)!+...+a[]*!+a[]*!
//a[i]为当前未出现的元素中是排在第几个(从0开始 )
比如,3124 是1~4全排列的第几个?(从0开始,比如1234是1~4全排列第0个)
X=*!+ *!+ *!+ *!=
- 第一位,在未出现的元素(1,2,3,4)中,只有2个数(1和2)比它小,位2~4全排列有3!个,所以=2*3!
- 第一位3,第二位1, 1在未出现的元素(1,2,4)中,只有0个数比它小,位3~4全排列有2!个,所以=0*2!
- 第一位3,第二位1,第三位, 2在未出现的元素(2,4)中,只有0个数比它小,所以=0*1!
- 第一位,第二位,第三位, 第四位,4在未出现的元素(4)中,只有0个数比它小,所以=0*0!
康拓展开代码(s[4]={3,1,2,4},n=4)
long int fac[]={,,,,,,,,,};//阶乘表
int congtuo(int s[],int n)
{
int i,j,temp,num;
num=;
for(i=;i<n;i++)
{
temp=;
for(int j=i+;j<n;j++)
if(s[j]<s[i]) //判断几个数小于它
temp++;
num+=fac[n-i-]*temp;
}
return num;
}
九宫格代码如下,纯手打勿喷:
#include <stdio.h>
#include <string.h> long int fac[]={,,,,,,,,,};//阶乘表 unsigned char step[]={}; // 9!=362880,所以数组要大点 char method[][]={{-,},{,},{,},{,-}}; //4种移动方法 struct node_t{
unsigned char data[];
}; struct node_t save_step[]; //保存移动数据,最多有 9!个移动数据 unsigned char end_p[]; //终点位置 int congtuo(unsigned char s[],int n)
{
int i,j,temp,num;
num=;
for(i=;i<n;i++)
{
temp=;
for(int j=i+;j<n;j++)
if(s[j]<s[i]) //判断几个数小于它
temp++;
num+=fac[n-i-]*temp;
}
return num;
} /*处理0函数
*返回值0:交换的位置非法,或被走过
*返回值1:没被走过
*返回值2:找到终点
*/
int handler_zero(int i,unsigned char data[])
{
int x,y,temp,num; for(int j=;j<;j++)
if(data[j]==)
{
/*[x,y]:需要交换的位置*/
x=j%+method[i][];
y=j/+method[i][]; /*判断交换位置是否越界*/
if(x<||x>)
return ;
else if(y<||y>)
return ; /*判断交换后的位置是否已被走过*/
data[j]= data[x+y*];
data[x+y*]=;
num=congtuo(data,);
if(step[num]==) //已被走过
{
return ;
} if(memcmp(end_p,data,)==) //找到终点
{
return ;
}
step[num]=;
return ;
}
} int start=,end=;
int bfs(void)
{
int x,y;
int next_end=end; //存放下个位置的标志位
int err;
unsigned char temp[];
for(;start<=end;start++)
{
for(int i=;i<;i++) //4种走法
{
memcpy(temp,(unsigned char *)save_step[start].data,); err=handler_zero(i,temp); //处理数据里的0 if(err) //保存数据
{
memcpy((unsigned char *)save_step[++next_end].data,temp,); if(err==) //找到终点
return ;
}
}
}
start=end+;
end=next_end;
return (+bfs());
} int main()
{
int step_num=; //步数
unsigned char s[]; printf("please enter start point:\r\n");
for(int i=;i<;i++)
{
scanf("%1d",&save_step[].data[i]);
} printf("please enter end point:\r\n");
for(int i=;i<;i++)
{
scanf("%1d",&end_p[i]);
}
step_num=bfs(); printf("%d\n",step_num); }
如果想看走的步数具体内容,该怎么办?
其实很简单,因为具体内容都保存在save_step[]里,我们只需要在node_t结构体里多定义一个标志位step_p,来指向上次步数的位置在哪.
代码如下:
#include <stdio.h>
#include <string.h> long int fac[]={,,,,,,,,,};//阶乘表 unsigned char step[]={}; // 9!=362880,所以数组要大点 char method[][]={{-,},{,},{,},{,-}}; //4种移动方法 struct node_t{
unsigned char data[];
unsigned int step_p;
}; struct node_t save_step[]; //保存移动数据,最多有 9!个移动数据 unsigned char end_p[]; //终点坐标 unsigned int end_index; //记录终点位置 int congtuo(unsigned char s[],int n)
{
int i,j,temp,num;
num=;
for(i=;i<n;i++)
{
temp=;
for(int j=i+;j<n;j++)
if(s[j]<s[i]) //判断几个数小于它
temp++;
num+=fac[n-i-]*temp;
}
return num;
} /*处理0函数
*返回值0:交换的位置非法,或被走过
*返回值1:没被走过
*返回值2:找到终点
*/
int handler_zero(int i,unsigned char data[])
{
int x,y,temp,num; for(int j=;j<;j++)
if(data[j]==)
{
/*[x,y]:需要交换的位置*/
x=j%+method[i][];
y=j/+method[i][]; /*判断交换位置是否越界*/
if(x<||x>)
return ;
else if(y<||y>)
return ; /*判断交换后的位置是否已被走过*/
data[j]= data[x+y*];
data[x+y*]=;
num=congtuo(data,);
if(step[num]==) //已被走过
{
return ;
} if(memcmp(end_p,data,)==) //找到终点
{
return ;
} step[num]=;
return ;
}
} int start=,end=;
int bfs(void)
{
int x,y;
int next_end=end; //存放下次bfs的end标志位
int err;
unsigned char temp[]; for(;start<=end;start++)
{
for(int i=;i<;i++) //4种走法
{
memcpy(temp,(unsigned char *)save_step[start].data,); err=handler_zero(i,temp); //处理数据里的0 if(err) //保存数据
{
memcpy((unsigned char *)save_step[++next_end].data,temp,); save_step[next_end].step_p=start; //记录上次步数位置. if(err==) //找到终点
{
end_index=next_end; //记录终点步数位置.
return ;
}
}
}
}
start=end+;
end=next_end;
return (+bfs());
} int main()
{
int step_num=; //步数
unsigned char s[]; printf("please enter start point:\r\n");
for(int i=;i<;i++)
{
scanf("%1d",&save_step[].data[i]);
} printf("please enter end point:\r\n");
for(int i=;i<;i++)
{
scanf("%1d",&end_p[i]);
} step_num=bfs();
printf("%d\n",step_num); /**打印步数具体内容**/
for(;step_num>=;step_num--)
{
printf("**step %d********\n",step_num);
for(int i=;i<;i++)
{
printf("%d %d %d\n",save_step[end_index].data[i*],
save_step[end_index].data[i*+],
save_step[end_index].data[i*+]);
}
end_index=save_step[end_index].step_p;
printf("\n");
} }
打印结果
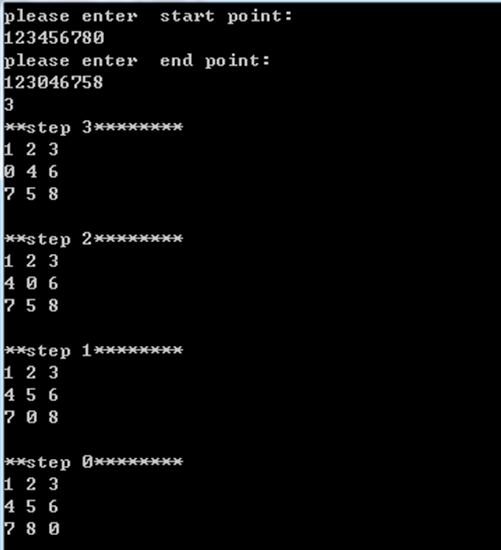
BFS-九宫格重排(详解)的更多相关文章
- BFS和DFS详解
BFS和DFS详解以及java实现 前言 图在算法世界中的重要地位是不言而喻的,曾经看到一篇Google的工程师写的一篇<Get that job at Google!>文章中说到面试官问 ...
- BFS和DFS详解以及java实现
前言 图在算法世界中的重要地位是不言而喻的,曾经看到一篇Google的工程师写的一篇<Get that job at Google!>文章中说到面试官问的问题中几乎有一半的问题都可以用图的 ...
- Leetcode之广度优先搜索(BFS)专题-详解429. N叉树的层序遍历(N-ary Tree Level Order Traversal)
Leetcode之广度优先搜索(BFS)专题-429. N叉树的层序遍历(N-ary Tree Level Order Traversal) 给定一个 N 叉树,返回其节点值的层序遍历. (即从左到右 ...
- BFS和DFS详解以及java实现(转载)
作者:Leo-Yang 原文都先发布在作者个人博客:http://www.leoyang.net/ 本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连 ...
- BFS详解
广度优先搜索详解 1. 也称宽度优先搜索,顾名思义,就是将一棵树一层一层往下搜.算法首先搜索和s距离为k的所有顶点,然后再去搜索和S距离为k+l的其他顶点.BFS是一种完备策略,即只 ...
- 图论中DFS与BFS的区别、用法、详解…
DFS与BFS的区别.用法.详解? 写在最前的三点: 1.所谓图的遍历就是按照某种次序访问图的每一顶点一次仅且一次. 2.实现bfs和dfs都需要解决的一个问题就是如何存储图.一般有两种方法:邻接矩阵 ...
- 图论中DFS与BFS的区别、用法、详解?
DFS与BFS的区别.用法.详解? 写在最前的三点: 1.所谓图的遍历就是按照某种次序访问图的每一顶点一次仅且一次. 2.实现bfs和dfs都需要解决的一个问题就是如何存储图.一般有两种方法:邻接矩阵 ...
- POJ 1077 Eight (BFS+康托展开)详解
本题知识点和基本代码来自<算法竞赛 入门到进阶>(作者:罗勇军 郭卫斌) 如有问题欢迎巨巨们提出 题意:八数码问题是在一个3*3的棋盘上放置编号为1~8的方块,其中有一块为控制,与空格相邻 ...
- 图文详解两种算法:深度优先遍历(DFS)和广度优先遍历(BFS)
参考网址:图文详解两种算法:深度优先遍历(DFS)和广度优先遍历(BFS) - 51CTO.COM 深度优先遍历(Depth First Search, 简称 DFS) 与广度优先遍历(Breath ...
随机推荐
- Hadoop学习笔记一
云帆大数据视频学习笔记,记录如下. 一.主机名设置的规范 /etc/hosts文件中添加如下的记录: 192.168.1.128 hadoop-yarn.cloudyhadoop.com had-ya ...
- BZOJ 3270: 博物馆 [概率DP 高斯消元]
http://www.lydsy.com/JudgeOnline/problem.php?id=3270 题意:一张无向图,一开始两人分别在$x$和$y$,每一分钟在点$i$不走的概率为$p[i]$, ...
- script 有哪个属性可以让它不立即执行 defer,async
.async 和 defer 属性 http://blog.csdn.net/qq_34986769/article/details/52155871 1. defer 属性<script sr ...
- SDN第5次上机作业
SDN第5次上机作业 实验目的 1.搭建如下拓扑并连接控制器 2.下发相关流表和组表实现负载均衡 3.抓包分析验证负载均衡 实验步骤 1.建立以下拓扑,并连接上ODL控制器. 提交要求:ODL拓扑界面 ...
- Windows下快速建立cocos2d-x项目
准备工作 1.根据当前系统版本,下载对应版本的Python 32位下载地址:http://www.python.org/ftp/python/2.7.5/python-2.7. ...
- dos命令(入门)
先说一下dos命令在很多情况下的共有特性 1.大小写一样,如dir和DIR 2.盘符后不加目录时,像"dir E:"和"dir E:\"没什么区别 3.使用形如 ...
- 织梦去除版权中的Power by DedeCms
找到文件 \include\dedesql.class.php 注释或删除下面代码,大概在588行 $arrs1 = array(0x63,0x66,0x67,0x5f,0x70,0x6f,0x77, ...
- 说说VNode节点(Vue.js实现)
写在前面 因为对Vue.js很感兴趣,而且平时工作的技术栈也是Vue.js,这几个月花了些时间研究学习了一下Vue.js源码,并做了总结与输出.文章的原地址:https://github.com/an ...
- cisco模拟器GNS3和虚拟机VMware的整合
微软和思科环境: 在思科认证的学习中,我们需要用到许多类的模拟器,但这些模拟器并不能够更真实的模拟我们的用户机在应用中所出现的现象.因此,我们借由微软的环境来更真实地体现我们所搭建的网络中的一些应用. ...
- 802.1X和NAP整合实验手册
实验描述 公司内部有多个部门,创建了域的架构,并搭建了DHCP服务器和Radius服务器,要求每个部门都独享一个网段,实现每位用户插上网线后,跳出窗体进行身份验证,如果用户通过验证,根据用户所在的部门 ...
