用Python学分析：集中与分散

散点图进阶，结合箱体图与直方图对数据形成全面的认识

描述数据集中趋势的分析量：

均值 - 全部数据的算术平均值

众数 - 一组数据中出现次数最多的变量值

中位数 - 一组数据经过顺序排列后处于中间位置上的变量值

描述数据离散程度的分析量：

方差 - 一组数据各变量值与其平均值离差平方和的平均数

标准差 - 方差的平方根

偏态 - 描述数据分布形态的统计量，其描述的是某总体取值分布的对称性。偏度 = 三阶中心距 / 标准差的三次方

峰度 - 描述总体中所有取值分布形态陡缓程度的统计量，这个统计量需要与正态分布相比较。 峰度 = 四阶中心距 / 方差平方（标准差四次方） - 3

描述性分析数据的计算：

 # 准备数据
 import numpy as np
 import matplotlib.pyplot as plt

 n = 1000
 x = np.random.randn(n)
 y = [int((item)*100) for item in np.random.randn( n )] #100以内的正整数随机数

 # 均值μ
 mu = np.mean(y)
 # 标准差δ  sigma = np.sqrt(np.sum(np.square( y - mu ))/n)
 sigma = np.std(y)
 # 峰度(公式准确度待确认)
 kurtosis = np.sum(np.power((y - mu),4))/(n) # 四阶中心距
 kurtosis = kurtosis / np.power(sigma,4)-3 # 峰度 = 四阶中心距 / 方差平方（标准差四次方） - 3
 # 偏度
 skewness = np.sum(np.power((y - mu),3))/(n) # 三阶中心距
 skewness = skewness / np.power(sigma,3) # 偏度 = 三阶中心距 / 标准差的三次方

 print(mu, sigma,skewness, kurtosis)

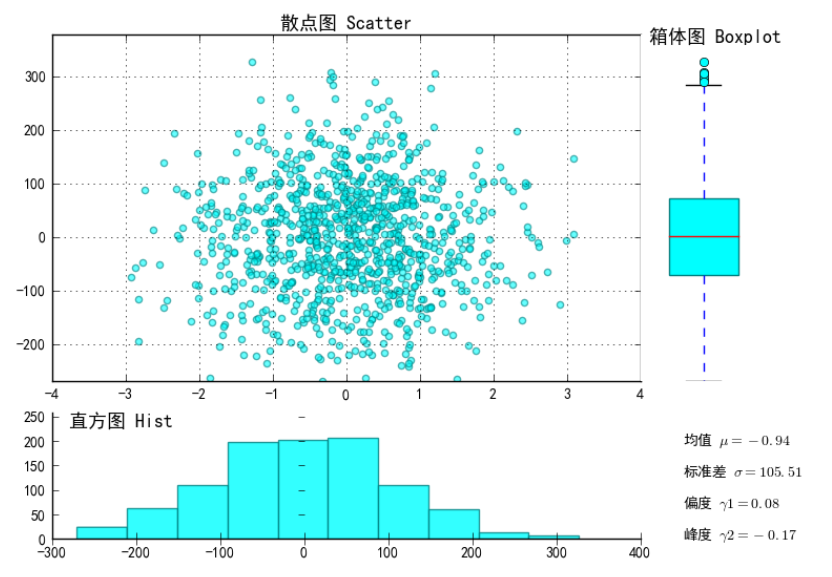
结果：

-0.944 105.50647783 0.0750892544722 -0.171492308767

图表显示

 # 图表显示
 fig = plt.figure( figsize = ( 8, 6 )) # 设置图表大小
 #设置图表的大小：[左, 下, 宽, 高] 规定的矩形区域 （全部是0~1之间的数，表示比例）
 rect_1 = [0.15, 0.30, 0.7,  0.55]
 rect_2 = [0.85, 0.30, 0.15, 0.55]
 rect_3 = [0.15, 0.05, 0.7,  0.2]
 fig_1 = plt.axes(rect_1) # 第一个图表
 fig_2 = plt.axes(rect_2) # 第二个图表
 fig_3 = plt.axes(rect_3) # 第三个图表
 #设置图表公共变量
 title_size = 13
 inner_color = 'cyan'
 outer_color = 'teal'
 # 第一个图表：散点图
 fig_1.scatter( x, y, s = 20, color = inner_color, edgecolor = outer_color, alpha = 0.6)
 fig_1.set_title('散点图 Scatter', fontsize = title_size)
 fig_1.set_ylim( min(y),max(y)+50 )
 fig_1.grid(True)

 # 第二个图表：箱体图
 fig_2.boxplot(y,
               widths = 0.55,
               patch_artist = True, # 要求用自定义颜色填充盒形图，默认白色填充
               boxprops = {'color':outer_color,'facecolor':inner_color, }, # 设置箱体属性，填充色和边框色
               flierprops = {'marker':'o','markerfacecolor':inner_color,'color':outer_color,}, # 设置异常值属性，点的形状、填充色和边框色
               meanprops = {'marker':'h','markerfacecolor':outer_color}, # 设置均值点的属性，点的形状、填充色
               medianprops = {'linestyle':'-','color':'red'} # 设置中位数线的属性，线的类型和颜色
              )
 fig_2.set_ylim( fig_1.get_ylim()) #设置箱体图与散点图同一纵坐标轴
 fig_2.get_yaxis().set_visible(False) #关闭坐标轴
 fig_2.get_xaxis().set_visible(False) #关闭坐标轴
 # 去除边框显示
 remove_col = ['top','bottom','left','right']
 for item in remove_col:
     fig_2.spines[item].set_visible(False)
     fig_2.spines[item].set_position(('data',0))
 fig.text(0.86, 0.84,'箱体图 Boxplot', fontsize = title_size )

 # 第三个图表：直方图
 n, bins, patches = fig_3.hist( y, color = inner_color, alpha = 0.8, edgecolor = outer_color )
 fig_3.set_ylim([0,max(n)+50])
 fig_3.spines['top'].set_visible(False) # 去除边框显示
 fig_3.spines['top'].set_position(('data',0)) # 去除边框刻度显示
 fig_3.spines['right'].set_color('none') # 去除边框显示
 fig_3.spines['right'].set_position(('data',0)) # 去除边框刻度显示
 fig.text(0.17, 0.23,'直方图 Hist', fontsize = title_size )

 # 文本信息
 fig.text(0.9, .20, '均值 $\mu = {0:.2f}$'.format(mu))
 fig.text(0.9, .15, '标准差 $\sigma = {0:.2f}$'.format(sigma))
 fig.text(0.9, .10, '偏度 $\gamma 1 = {0:.2f}$'.format(skewness))
 fig.text(0.9, .05, '峰度 $\gamma 2 = {0:.2f}$'.format(kurtosis))
 plt.show()

结果：