Machine Learning系列--归一化方法总结

一、数据的标准化（normalization）和归一化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

目前数据标准化方法有多种，归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法，对系统的评价结果会产生不同的影响，然而不幸的是，在数据标准化方法的选择上，还没有通用的法则可以遵循。

1.1 归一化的目标：统一量纲

归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为纯量。 比如，复数阻抗可以归一化书写：$Z=R+j\omega L=R(1+j\omega L/R)$，复数部分变成了纯数量了，没有量纲。

另外，微波之中也就是电路分析、信号系统、电磁波传输等，有很多运算都可以如此处理，既保证了运算的便捷，又能凸现出物理量的本质含义。

1.2 归一化后有两个好处

1. 提升模型的收敛速度

如下图，$x_1$的取值为0-2000，而$x_2$的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快（理解：也就是步长走多走少方向总是对的，不会走偏）。

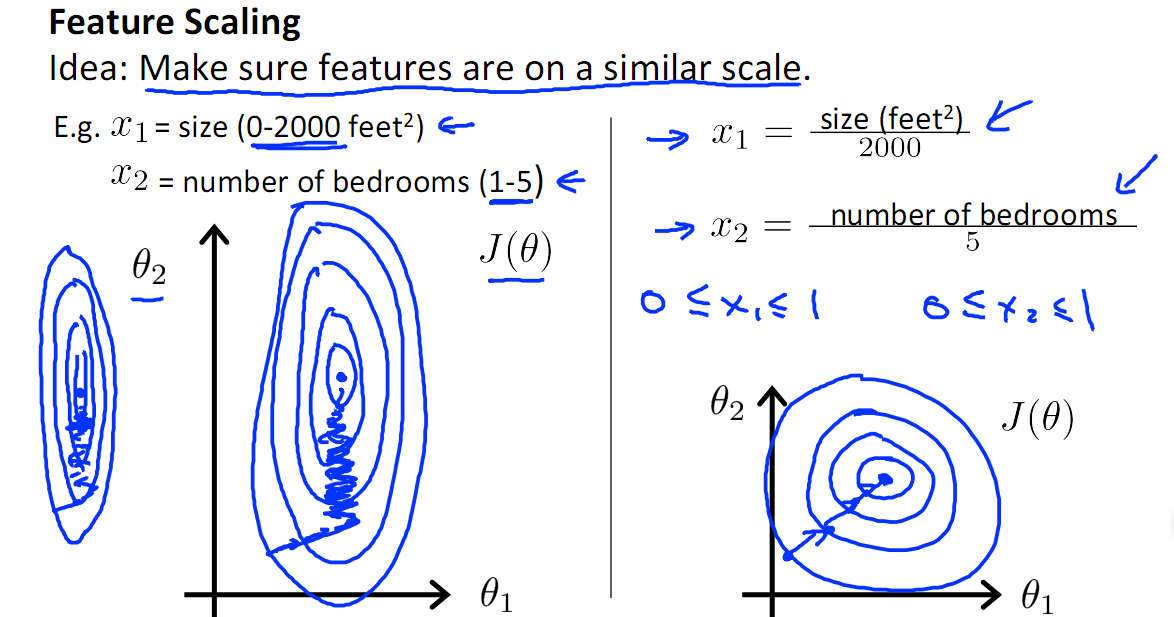
2.提升模型的精度

归一化的另一好处是提高精度，这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，上图中$x_2$的取值范围比较小，涉及到距离计算时其对结果的影响远比$x_1$带来的小，所以这就会造成精度的损失。所以归一化很有必要，他可以让各个特征对结果做出的贡献相同。

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。

在数据分析之前，我们通常需要先将数据标准化（normalization），利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。

从经验上说，归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。

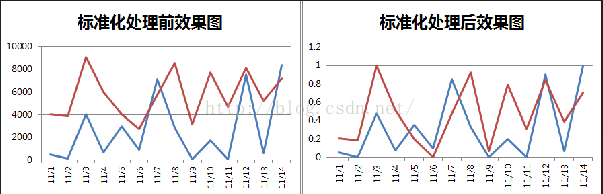
3. 深度学习中数据归一化可以防止模型梯度爆炸。

二、数据需要归一化的机器学习算法

1. 需要归一化的模型：
有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM（距离分界面远的也拉近了，支持向量变多？）。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。2. 有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression（因为θ的大小本来就自学习出不同的feature的重要性吧？）。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

2. 不需要归一化的模型：
概率模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、rf。而像adaboost、gbdt、xgboost、svm、lr、KNN、KMeans之类的最优化问题就需要归一化。

三、常见的数据归一化方法

3.1 min-max标准化(Min-max normalization)/0-1标准化(0-1 normalization)/线性函数归一化/离差标准化

对原始数据的线性变换，使结果落到[0,1]区间，转换函数如下：

$${x^ * } = \frac{{x - {x_{min}}}}{{{x_{max}} - {x_{min}}}}.$$

其中$x_{max}$为样本数据的最大值，$x_{min}$为样本数据的最小值。

这种方法有一个缺陷就是当有新数据加入时，可能导致$x_{max}$和$x_{min}$的变化，需要重新定义。

3.2 z-score 标准化(zero-mean normalization)

最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法，spss默认的标准化方法就是z-score标准化。

也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。

经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：

$$ {x^* } = \frac{{x - \mu }}{\sigma }. $$

这两种最常用方法使用场景：

1、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
原因是使用第一种方法(线性变换后)，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。
而在第二种归一化方式中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。

线性变换后协方差产生倍数值缩放推导如下：

假设数据为2个维度$(X, Y)$，为方便分析，取线性系数$c$，线性变换后的$x'$和$y'$分别为：

$$x' = {c_x} \cdot x.$$

$$y' = {c_y} \cdot y.$$

计算协方差:

$${{\sigma '}_{xy}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {{c_x}{x_i} - {c_x}\bar x} \right)} \left( {{c_y}{y_i} - {c_y}\bar y} \right) = {c_x}{c_y}{\sigma _{xy}} \ne {\sigma _{xy}}.$$

可以看到，使用第一种方法(线性变换后)，其协方差产生了${c_x}{c_y}$倍的缩放。

3.3 log函数转换

通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

$${x^ * } = \frac{{{{log }_{10}}\left( x \right)}}{{{{log }_{10}}\left( {{x_{max }}} \right)}}.$$

看了下网上很多介绍都是${x^ * } = {log _{10}}\left( x \right)$，其实是有问题的，这个结果并非一定落到[0,1]区间上，应该还要除以${log _{10}}\left( {{x_{max }}} \right)$，$x_{max }$为样本数据最大值，并且所有的数据都要大于等于1。

3.4 atan函数转换

用反正切函数也可以实现数据的归一化:

$$ {x^ * } = \frac{{atan \left( x \right) * 2}}{\pi }. $$

使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上，而并非所有数据标准化的结果都映射到[0,1]区间上。

3.5 Decimal scaling小数定标标准化

这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性$A$的取值中的最大绝对值。

将属性$A$的原始值$x$使用decimal scaling标准化到$x^ * $的计算方法是：

$$x^ * =\frac{x}{10^j}.$$
其中，$j$是满足条件的最小整数。
例如,假定$A$的值由-986到917，$A$的最大绝对值为986，为使用小数定标标准化，我们用每个值除以1000（即，$j=3$），这样，-986被规范化为-0.986。
注意，标准化会对原始数据做出改变，因此需要保存所使用的标准化方法的参数，以便对后续的数据进行统一的标准化。

3.6 模糊量化模式

$$ {x^ * } = \frac{1}{2} + \frac{1}{2} \cdot sin \left( {\frac{{x - \frac{{{x_{max }} - {x_{min }}}}{2}}}{{{x_{max }} - {x_{min }}}} \cdot \pi } \right). $$

参考博客：

1. 数据标准化/归一化normalization：https://blog.csdn.net/pipisorry/article/details/52247379.