初窥ThinkPHP

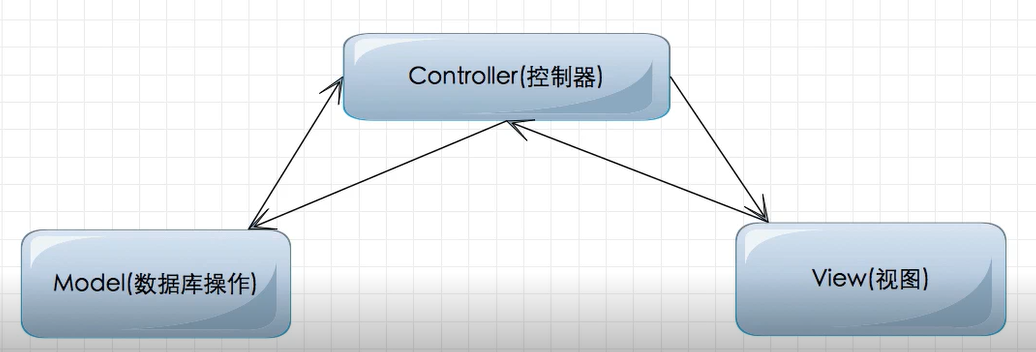
MVC全称(Model View Controller)

Model:模型（可以理解位数据库操作模型）

View:视图（视图显示）

Controller:（控制器）

简单的说框架就是一个类的集合。集合了十分多的类。

注：一般类中加了action的就是控制器 model的就是数据库操作方面的。

Thinkphp的安装：

先去thinkphp官网下载框架回来：http://www.thinkphp.cn/donate/download/id/870.html

完整包和核心包的区别在于核心包只有一些核心文件，完整包就包括了一些常规的扩展库。

　　首先得有一个thinkphp的入口。网站的根目录新建立一个thinkphp的文件夹然后将thinkphp的文件放进去。再到根目录新建index.php的php文件。

建立如下代码即可完成安装

1 2 3 4 5 6

<?php define('APP_NAME', 'index');   //前台项目的名称 define('APP_PATH','./index/'); //前台项目的路劲 define('RUNTIME_PATH', APP_PATH .'temp/'); //runtime的路径 @include './Thinkphp/ThinkPHP.php'; //引入thinkphp的运行文件。 ?>

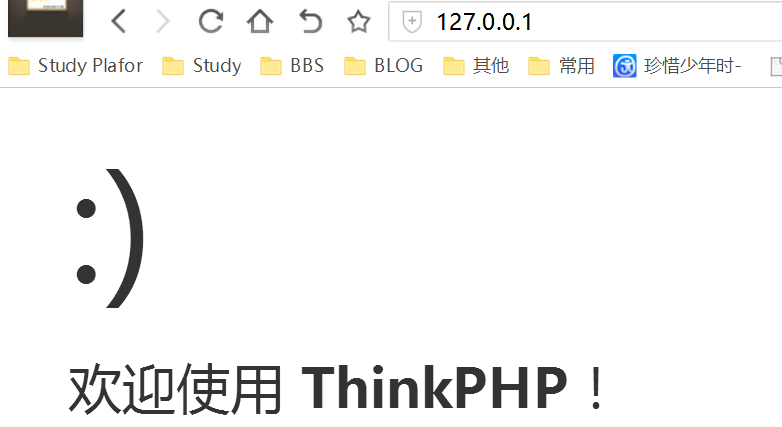
访问127.0.0.1效果如下所示：

浏览根目录你会发现多了一个文件夹：

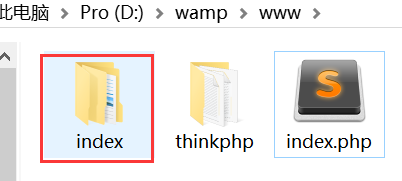
便是index这个文件夹。该文件夹就是index.php定义的那个index了。

在index\Lib\Action\IndexAction.class.php文件夹为控制器。

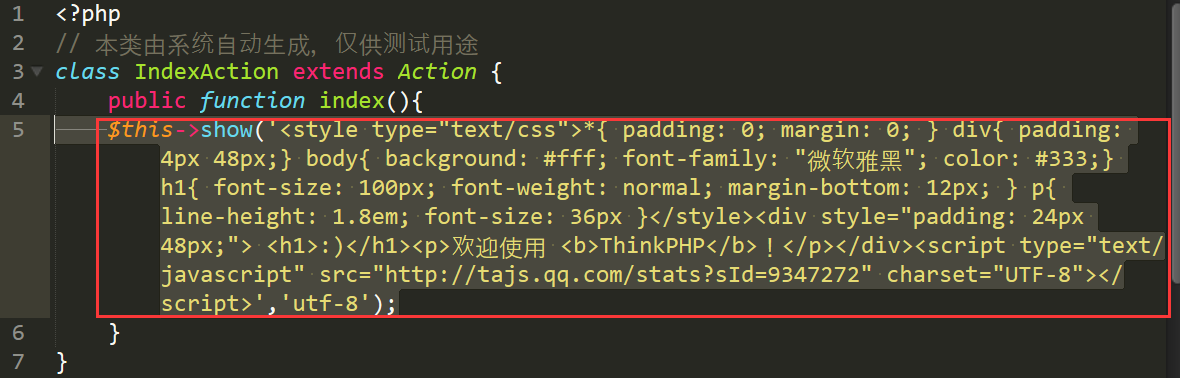
第五行的代码就是我们在127.0.0.1首页看到的效果。

如果更改那么前台页面也随之更改。我改为下图