树链剖分+线段树 HDOJ 4897 Little Devil I（小恶魔）

题目链接

题意：

　　给定一棵树，每条边有黑白两种颜色，初始都是白色，现在有三种操作：

　　　　1 u v：u到v路径（最短）上的边都取成相反的颜色

　　　　2 u v：u到v路径上相邻的边都取成相反的颜色（相邻即仅有一个节点在路径上）

　　　　3 u v：查询u到v路径上有多少个黑色边

思路：

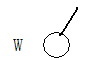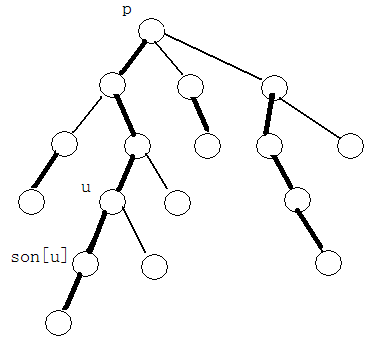
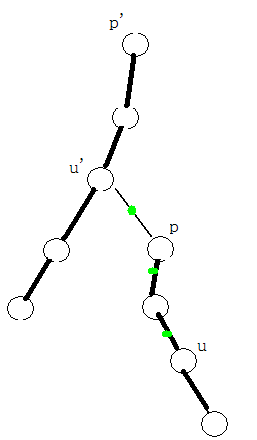
　　对树进行树链剖分，分成重链和轻链，用两棵线段树W，L来维护。W维护树上在重链上的u和v之间的边的翻转情况（操作在线段树上的[pos[v],pos[u]]区间）；L维护树上在重链上的u和v之间的相邻边的翻转情况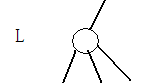。那么某一个点u与它父亲节点fa[u]的边的最终翻转情况为：W(pos[u], pos[u])（如果边是重链上的边），W(pos[u], pos[u])^L(pos[fa[u]], pos[fa[u]])（如果边是轻链）。对于1操作，只要简单的在W上维护就可以了。对于2操作，除了在L上操作，还要注意头和尾的特殊处理（因为对于重链内的点，不包括头尾，只在W上查询），也就是u的重链上的儿子son[u]以及u的链头p=belong[u]要在W上翻转一次，结合图可能更能理解。还有就是线段树的操作了。

另外：

　　u可能没有son[u]，默认为虚点0，那么在线段树上需要加上一句话：if (l == r) return ;

#include <bits/stdc++.h>
 
const int N = 1e5 + 5;
 
//线段树
#define lson l, mid, o << 1
#define rson mid + 1, r, o << 1 | 1
struct Seg_Tree {
    int fp[N<<2], s[N<<2];
    void flip(int l, int r, int o) {
        s[o] = (r - l + 1) - s[o];
        fp[o] ^= 1;
    }
    void push_up(int o) {
        s[o] = s[o<<1] + s[o<<1|1];
    }
    void push_down(int l, int r, int o) {
        if (fp[o]) {
            int mid = l + r >> 1;
            flip (lson);
            flip (rson);
            fp[o] = 0;
        }
    }
    void build(int l, int r, int o) {
        fp[o] = s[o] = 0;
        if (l == r) {
            return ;
        }
        int mid = l + r >> 1;
        build (lson);
        build (rson);
    }
    void updata(int ql, int qr, int l, int r, int o) {
        if (ql <= l && r <= qr) {
            flip (l, r, o);
            return ;
        }
        if (l == r) return ;  //!
        push_down (l, r, o);
        int mid = l + r >> 1;
        if (ql <= mid) updata (ql, qr, lson);
        if (qr > mid) updata (ql, qr, rson);
        push_up (o);
    }
    int query(int ql, int qr, int l, int r, int o) {
        if (ql <= l && r <= qr) {
            return s[o];
        }
        push_down (l, r, o);
        int mid = l + r >> 1, ret = 0;
        if (ql <= mid) ret += query (ql, qr, lson);
        if (qr > mid) ret += query (ql, qr, rson);
        push_up (o);
        return ret;
    }
}W, L;
 
std::vector<int> edge[N];
int sz[N], dep[N], son[N], fa[N];
int pos[N], belong[N];
int loc;
int n;
 
int query(int u, int v) {
    int p = belong[u], q = belong[v], ret = 0;
    while (p != q) {
        if (dep[p] < dep[q]) {
            std::swap (p, q);
            std::swap (u, v);
        }
        if (u != p) {
            ret += W.query (pos[son[p]], pos[u], 1, n, 1);
        }
        ret += (W.query (pos[p], pos[p], 1, n, 1) ^ L.query (pos[fa[p]], pos[fa[p]], 1, n, 1));
        u = fa[p];
        p = belong[u];
    }
 
    if (u == v) return ret;
 
    if (dep[u] < dep[v]) {
        std::swap (u, v);
    }
    ret += W.query (pos[son[v]], pos[u], 1, n, 1);
    return ret;
}
 
void modify(int t, int u, int v) {
    int p = belong[u], q = belong[v];
    while (p != q) {
        if (dep[p] < dep[q]) {
            std::swap (p, q);
            std::swap (u, v);
        }
        if (t == 1) {
            W.updata (pos[p], pos[u], 1, n, 1);
        } else {
            L.updata (pos[p], pos[u], 1, n, 1);
            W.updata (pos[son[u]], pos[son[u]], 1, n, 1);
            W.updata (pos[p], pos[p], 1, n, 1);
        }
        u = fa[p];
        p = belong[u];
    }
 
    if (dep[u] < dep[v]) {
        std::swap (u, v);
    }
    if (t == 1) {
        if (u == v) return ;
        W.updata (pos[son[v]], pos[u], 1, n, 1);
    } else {
        L.updata (pos[v], pos[u], 1, n, 1);
        W.updata (pos[son[u]], pos[son[u]], 1, n, 1);
        W.updata (pos[v], pos[v], 1, n, 1);
    }
}
 
//树链剖分
void DFS2(int u, int chain) {
    pos[u] = ++loc;
    belong[u] = chain;
    if (son[u]) {
        DFS2 (son[u], chain);
    }
    for (auto v: edge[u]) {
        if (v == fa[u] || v == son[u]) continue;
        DFS2 (v, v);
    }
}
 
void DFS1(int u, int pa) {
    sz[u] = 1; dep[u] = dep[pa] + 1;
    son[u] = 0; fa[u] = pa;
    for (auto v: edge[u]) {
        if (v == pa) continue;
        DFS1 (v, u);
        sz[u] += sz[v];
        if (sz[son[u]] < sz[v]) son[u] = v;
    }
}
 
void prepare() {
    sz[0] = dep[0] = fa[0] = 0;
    DFS1 (1, 0);
    loc = 0;
    DFS2 (1, 1);
    W.build (1, n, 1);
    L.build (1, n, 1);
}
 
void init_edge(int n) {
    for (int i=1; i<=n; ++i) {
        edge[i].clear ();
    }
}
 
int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        scanf ("%d", &n);
 
        init_edge (n);
        for (int i=1; i<n; ++i) {
            int u, v;
            scanf ("%d%d", &u, &v);
            edge[u].push_back (v);
            edge[v].push_back (u);
        }
 
        prepare ();
 
        int q;
        scanf ("%d", &q);
        while (q--) {
            int t, u, v;
            scanf ("%d%d%d", &t, &u, &v);
            if (t == 3) {
                printf ("%d\n", query (u, v));
            } else {
                modify (t, u, v);
            }
        }
    }
    return 0;
}