洛谷 P2015 二叉苹果树(codevs5565) 树形dp入门

dp这一方面的题我都不是很会，所以来练(xue)习(xi)，大概把这题弄懂了。

树形dp就是在原本线性上dp改成了在 '树' 这个数据结构上dp。

一般来说，树形dp利用dfs在回溯时进行更新，使用儿子节点对父亲节点进行更新。

树形dp很多题需要在二叉树上进行。

进入正题。

点我看题

这个图是洛谷题面里奇奇怪怪的东西，格式弄好就这样。

题意：有一棵已知根(1)的二叉树，每条边都有一个权值，现在可以保留 q 条边，问在这样的前提下，以 1 为根 的树最多能有多少权值和。

题意可以画个图来解释

这个就是样例的图，假设我萌只保留 1-->3 这条边，辣么我萌得到的权值是 1-->3 这条边的权值。

　　　　　　　　　假设我萌只断掉 1-->3 这条边，辣么可以得到的权值只有1-->4这条边，因为如果1-->3没了，2,5节点无法连通到1，

　　　　　　      3-->2   3-->5 的边也就不是以1为根的树里的了。

思路：这题看到了二叉树，于是可以往dp方向思考一下，发现是可行的。

首先可以把所以边的权值下移到节点上，这样我萌列出转移方程。

设f[i,j]表示以 i 为根的子树中，保留了 j  个节点得到的最大权值。

　　 设 i 的左儿子为son[i,1] 右儿子为son[i,2]　设权值下移后 x 节点的权值为cost[x]

　　　则对于 某个节点  x 来说，有三种选择，一是选了左儿子这个点，不选右儿子。

　                                                                        二是选了右儿子这个点，不选左儿子。

　　　　　　　　　　　　　　　　　　　　  三是既选左儿子又选右儿子。

辣么分别列出转移方程： ① f[i,j]=max(f[son[i,1],j-1]+cost[son[i,1]])  (如果选了son[i,1]则把该权值加上，因为枚举的 j 表示的是保留 j 个节点，所以要保留son[i,1]的情况下,就要找他的前驱状态 j-1 )

　　　　　　　　　　　 ② f[i,j]=max(f[son[i,2],j-1]+cost[son[i,2]]) (这个和①是类似的，只是将左儿子改为右儿子)

　　　　　　　　　　　 ③ f[i,j]=max(f[son[i,1],k]+f[son[i,2],j-2-k]+cost[son[i,1]+cost[son[i,2]) (这个看起来就要复杂得多，我萌画图看看)

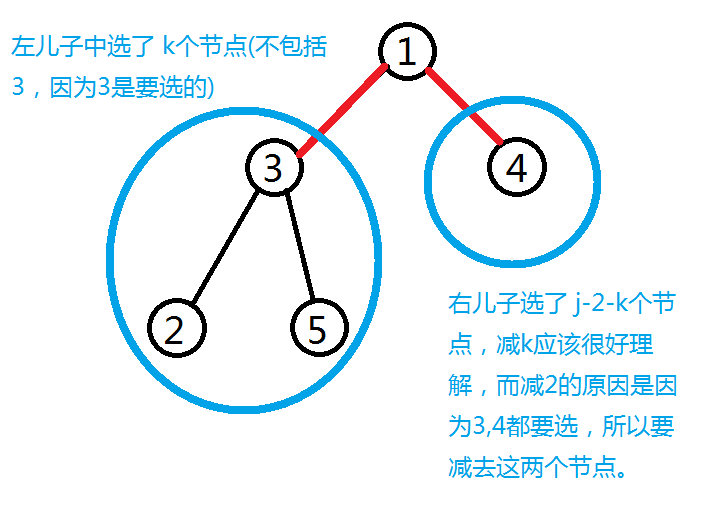
这样的话应该会很清晰了，辣么肿么去跑这个dp捏。

显然我萌要先做一个预处理，用递归先把 cost[i] son[i,1] son[i,2] 预处理出来。

然后在用一个dfs递归进行dp。 对于 ①②两种情况可以在遍历边的时候直接进行更新，但是对于③情况要在边遍历完后进行。

为什么？ 由于递归的顺序。比如样例这个图，他的顺序是这样的   1-->3-->2 好这里可以对2节点的f[2,j]进行更新了

　　　　　　　　　　        然后 1-->3-->2-->3(回溯同时用2节点的信息进行①情况的更新)-->5-->3(此时3的边都遍历完了，先是用5节点的信息进行②情况的更新,然后再使用 2 和 5 的节点信息一起对3进行③情况更新)-->1(类似，用3对1进行①情况的更新) -->4-->1(类似，用4对1进行②情况的更新，用3 4对1进行③情况更新)

这样就应该理解为什么要先把边遍历完才更新③情况了，因为只有这样，要更新的节点的左右儿子的信息才是都已知的，这样才能更新，满足了dp需要利用前驱信息。

 type
   node=record
       y,z:longint;
       next:longint;
   end;
 var num,father,first,cost:array[..]of longint;
     son:Array[..,..]of longint;
     i:longint;
     n,q:longint;
     x,y,z:longint;
     tot:longint;
     e:Array[..]of node;
     f:array[..,..]of longint;
 function max(a,b:longint):longint;
 begin
   if a>b then exit(a) else exit(b);
 end;
 procedure adde(x,y,z:longint);
 begin
   e[tot].next:=first[x];
   e[tot].y:=y;
   e[tot].z:=z;
   first[x]:=tot;
   inc(tot);
 end;
 procedure buildtree(x:longint);
 var i,y:longint;
 begin
   i:=first[x];
   while i<>- do
   begin
     y:=e[i].y;
     if father[y]= then
     begin
       father[y]:=x;
       cost[y]:=e[i].z;
       inc(num[x]);
       son[x,num[x]]:=y;
       buildtree(y);
     end;
     i:=e[i].next;
   end;
 end;
 procedure dfs(x:longint);
 var i,j:longint;
     l,r,y:longint;
 begin
   for i:= to num[x] do
   begin
     y:=son[x,i];
     dfs(y);
     for j:= to q do
     f[x,j]:=max(f[x,j],f[y,j-]+cost[y]);
   end;
   l:=son[x,];
   r:=son[x,];
   for i:= to q do
     for j:= to i- do
     f[x,i]:=max(f[x,i],f[l,j]+f[r,i--j]+cost[l]+cost[r]);
 end;
 begin
   read(n,q);
   for i:= to n do
   first[i]:=-;
   for i:= to n- do
   begin
     read(x,y,z);
     adde(x,y,z);
     adde(y,x,z);
   end;
   father[]:=;
   buildtree();
   dfs();
   writeln(f[,q]);
 end.

树形dp

这题的话，我理解了挺久的，然后理解后直接就敲了一个代码，然后一次过了，所以理解有时候会让代码更快实现。

版权声明：要转载请在评论区留言=v=