Keras 回归 拟合 收集

案例1

 from keras.models import Sequential
 from keras.layers import Dense, LSTM, Activation
 from keras.optimizers import adam, rmsprop, adadelta
 import numpy as np
 import matplotlib.pyplot as plt
 #construct model
 models = Sequential()
 models.add(Dense(100, init='uniform',activation='relu' ,input_dim=1))
 models.add(Dense(50, activation='relu'))
 models.add(Dense(1,activation='tanh'))
 adamoptimizer = adam(lr=0.001, beta_1=0.9, beta_2=0.999, decay=0.00001)
 models.compile(optimizer='rmsprop', loss='mse',metrics=["accuracy"] )

 #train data
 dataX = np.linspace(-2 * np.pi,2 * np.pi, 1000)
 dataX = np.reshape(dataX, [dataX.__len__(), 1])
 noise = np.random.rand(dataX.__len__(), 1) * 0.1
 dataY = np.sin(dataX) + noise

 models.fit(dataX, dataY, epochs=100, batch_size=10, shuffle=True, verbose = 1)
 predictY = models.predict(dataX, batch_size=1)
 score = models.evaluate(dataX, dataY, batch_size=10)

 print(score)
 #plot
 fig, ax = plt.subplots()
 ax.plot(dataX, dataY, 'b-')
 ax.plot(dataX, predictY, 'r.',)

 ax.set(xlabel="x", ylabel="y=f(x)", title="y = sin(x),red:predict data,bule:true data")
 ax.grid(True)

 plt.show()

案例2：

 import numpy as np

 import random
 from sklearn.preprocessing import MinMaxScaler
 import matplotlib.pyplot as plt
 from keras.models import Sequential
 from keras.layers import Dense,Activation
 from keras.optimizers import Adam,SGD

 X = np.linspace(1,20,1000)
 X = X[:,np.newaxis]
 y = np.sin(X) + np.random.normal(0,0.08,(1000,1))
 min_max_scaler = MinMaxScaler((0,1))
 y_train = min_max_scaler.fit_transform(y)
 x_train = min_max_scaler.fit_transform(X)

 model1=Sequential()
 model1.add(Dense(1000,input_dim = 1))
 model1.add(Activation('relu'))
 model1.add(Dense(1))
 model1.add(Activation('sigmoid'))
 adam = Adam(lr = 0.001)
 sgd = SGD(lr = 0.1,decay=12-5,momentum=0.9)
 model1.compile(optimizer = adam,loss = 'mse')
 print('-------------training--------------')
 model1.fit(x_train,y_train,batch_size= 12,nb_epoch = 500,shuffle=True)
 Y_train_pred=model1.predict(x_train)
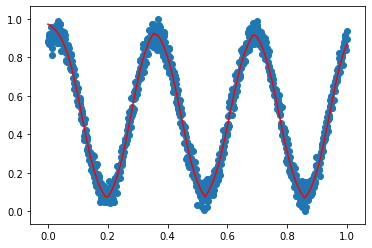
 plt.scatter(x_train,y_train)
 plt.plot(x_train,Y_train_pred,'r-')
 plt.show()

案例3

 #加激活函数的方法2：model.add(Dense(units=10,input_dim=1,activation=' '))
 from keras.optimizers import SGD
 from keras.layers import Dense,Activation
 #构建一个顺序模型
 model=Sequential()

 #在模型中添加一个全连接层
 #units是输出维度,input_dim是输入维度(shift+两次tab查看函数参数)
 #输入1个神经元,隐藏层10个神经元,输出层1个神经元
 model.add(Dense(units=10,input_dim=1,activation='relu'))   #增加非线性激活函数
 model.add(Dense(units=1,activation='relu'))   #默认连接上一层input_dim=10

 #定义优化算法(修改学习率)
 defsgd=SGD(lr=0.3)

 #编译模型
 model.compile(optimizer=defsgd,loss='mse')   #optimizer参数设置优化器,loss设置目标函数

 #训练模型
 for step in range(3001):
     #每次训练一个批次
     cost=model.train_on_batch(x_data,y_data)
     #每500个batch打印一个cost值
     if step%500==0:
         print('cost:',cost)

 #打印权值和偏置值
 W,b=model.layers[0].get_weights()   #layers[0]只有一个网络层
 print('W:',W,'b:',b)

 #x_data输入网络中，得到预测值y_pred
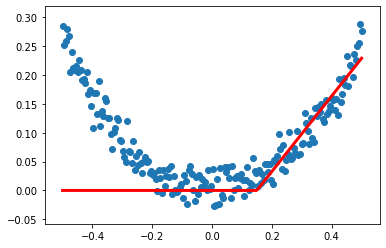
 y_pred=model.predict(x_data)

 plt.scatter(x_data,y_data)

 plt.plot(x_data,y_pred,'r-',lw=3)
 plt.show()

案例4：

 #加激活函数的方法1：mode.add(Activation(''))
 from keras.optimizers import SGD
 from keras.layers import Dense,Activation
 import numpy as np

 np.random.seed(0)
 x_data=np.linspace(-0.5,0.5,200)
 noise=np.random.normal(0,0.02,x_data.shape)
 y_data=np.square(x_data)+noise

 #构建一个顺序模型
 model=Sequential()

 #在模型中添加一个全连接层
 #units是输出维度,input_dim是输入维度(shift+两次tab查看函数参数)
 #输入1个神经元,隐藏层10个神经元,输出层1个神经元
 model.add(Dense(units=10,input_dim=1))
 model.add(Activation('tanh'))   #增加非线性激活函数
 model.add(Dense(units=1))   #默认连接上一层input_dim=10
 model.add(Activation('tanh'))

 #定义优化算法(修改学习率)
 defsgd=SGD(lr=0.3)

 #编译模型
 model.compile(optimizer=defsgd,loss='mse')   #optimizer参数设置优化器,loss设置目标函数

 #训练模型
 for step in range(3001):
     #每次训练一个批次
     cost=model.train_on_batch(x_data,y_data)
     #每500个batch打印一个cost值
     if step%500==0:
         print('cost:',cost)

 #打印权值和偏置值
 W,b=model.layers[0].get_weights()   #layers[0]只有一个网络层
 print('W:',W,'b:',b)

 #x_data输入网络中，得到预测值y_pred
 y_pred=model.predict(x_data)

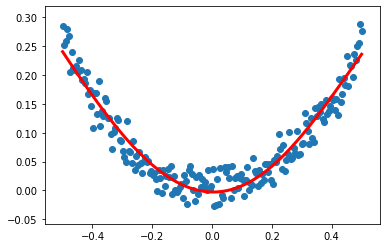
 plt.scatter(x_data,y_data)

 plt.plot(x_data,y_pred,'r-',lw=3)
 plt.show()

案列5

 import numpy as np
 import matplotlib.pyplot as plt
 from keras.models import Sequential
 from keras.layers import Dense
 from keras.optimizers import Adam

 np.random.seed(0)
 points = 500
 X = np.linspace(-3, 3, points)
 y = np.sin(X) + np.random.uniform(-0.5, 0.5, points)

 model = Sequential()
 model.add(Dense(50, activation='sigmoid', input_dim=1))
 model.add(Dense(30, activation='sigmoid'))
 model.add(Dense(1))
 adam = Adam(lr=0.01)
 model.compile(loss='mse', optimizer=adam)
 model.fit(X, y, epochs=50)

 predictions = model.predict(X)
 plt.scatter(X, y)
 plt.plot(X, predictions, 'ro')
 plt.show()

案列6：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
x = list(np.arange(0,4,0.1))
#给3次多项式添加噪音
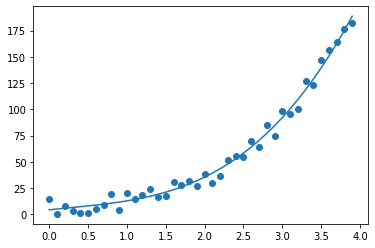
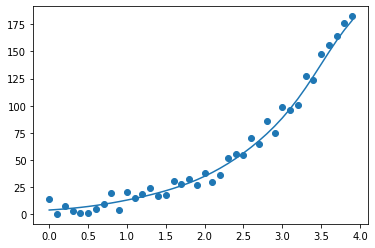
y = list(map(lambda val: val**3*3 + np.random.random()*20 , x) )

plt.scatter(x, y)

#指明用3次多项式匹配
w = np.polyfit (x, y, 3)
fn = np.poly1d(w)

#打印适配出来的参数和函数
print(w)
print(fn)

plt.plot(x, fn(x))

案列7

 1 %matplotlib inline
 2 import matplotlib.pyplot as plt
 3 from keras.datasets import mnist
 4 from keras.models import Sequential
 5 from keras.layers.core import Dense, Activation
 6 from keras.layers.advanced_activations import LeakyReLU, PReLU
 7 from keras.optimizers import SGD
 8
 9 x = list(np.arange(0,4,0.1))
10 #给3次多项式添加噪音
11 y = list(map(lambda val: val**3*3 + np.random.random()*20 , x) )
12
13 model = Sequential()
14 #神经元个数越多,效果会越好,收敛越快,太少的话难以收敛到所需曲线
15 model.add(Dense(100, input_shape=(1,)))
16
17 #Relu,得到的是一条横线
18 #Tanh,稍稍好于Relu,但是拟合的不够
19 #sigmoid, 只要神经元个数足够(50+),训练1000轮以上,就能达到比较好的效果
20 model.add(Activation('sigmoid'))
21 #model.add(LeakyReLU(alpha=0.01))
22 #model.add(Dense(3))
23
24 model.add(Dense(1))
25 model.compile(optimizer="sgd", loss="mse")
26 model.fit(x, y, epochs=2000, verbose=0)
27
28 print(type(fn(3)))
29 print(fn(1))
30 print(fn(3))
31
32 plt.scatter(x, y)
33 plt.plot(x, model.predict(x))