AtCoder ARC061E Snuke's Subway Trip 最短路
(有任何问题欢迎留言或私聊 && 欢迎交流讨论哦
Catalog
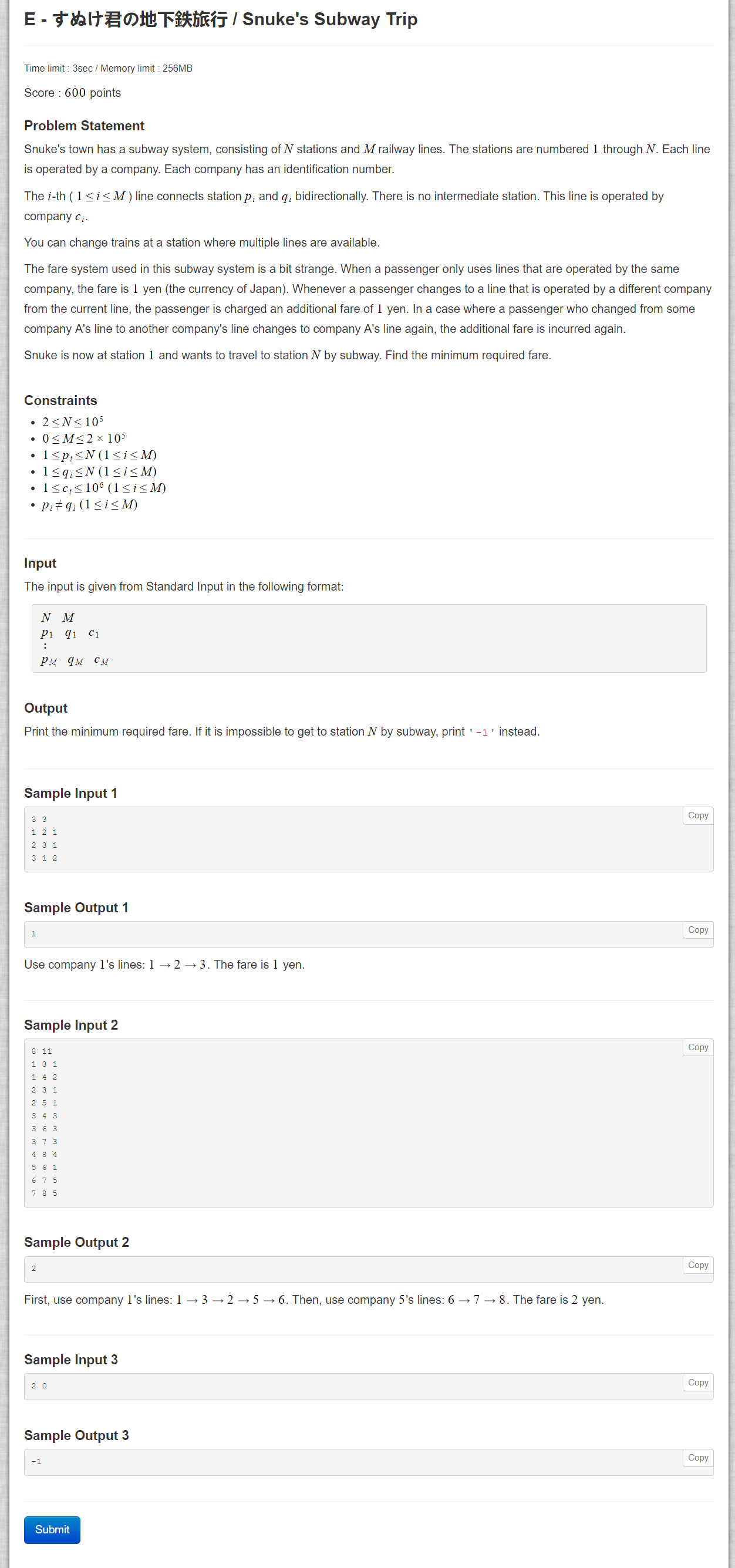
Problem:传送门
原题目描述在最下面。
\(n(1e5)\)个点, \(m(2e5)\)条边, 每条边有一个属性值。经过一条同一属性值的连续路径花费为1。问从1到n的最小花费。
Solution:
我的解法
直接边最短路搞,然后t的飞起。仔细一想,这样写的话有\(2e5\)个点,边数更是多到飞起,拿命跑啊,不过代码我还是放下面。
正解:拆点
把一条\(u->v\)属性为\(c\)的路径,拆成\(u->uc, uc->vc, vc->v\)三条路径,边权分别为\(1, 0, 1\)。
然后跑最裸的最短路就行,答案除\(2\)输出。
why?
为什么这样是对的呢?
对于一个点连接的许多路径,从一条走向另一条,如果属性相同就不需要额外花费。这点怎么做到的呢?
比如\(x->y,y->z\)属性均为\(c\):实际路径是\(x->yc->z\),经过了yc这个中间点,而且没有额外的花费。
答案除\(2\)是因为出发和结束都算了一遍花费。
AC_Code:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int MXN = 1e6 + 5;
const int MXT = 2e7 + 6;
const uLL base = 99959;
unordered_map<uLL, int> mp;
int n, m, tn;
int head[MXN], tot;
struct lp {
int v, c, nex;
}cw[MXT];
int dis[MXT], vis[MXT], fa[MXN];
void add_edge(int u,int v,int w) {
cw[++tot].v = v;cw[tot].c = w;cw[tot].nex = head[u];
head[u] = tot;
cw[++tot].v = u;cw[tot].c = w;cw[tot].nex = head[v];
head[v] = tot;
}
void dij() {
priority_queue<pii,vector<pii>,greater<pii> >Q;
for(int i = 1; i <= n; ++i) dis[i] = INF, vis[i] = 0;
dis[1] = 0;
Q.push({dis[1], 1});
while(!Q.empty()) {
pii now = Q.top();Q.pop();
int u = now.se;
if(vis[u]) continue;
vis[u] = 1;
for(int i = head[u]; ~i; i = cw[i].nex) {
int v = cw[i].v;
//if(vis[v]) continue;
if(dis[v] > dis[u] + cw[i].c) {
dis[v] = dis[u] + cw[i].c;
Q.push({dis[v], v});
}
}
}
int ans = dis[tn];
while(!Q.empty()) Q.pop();
if(ans == INF) ans = -2;
printf("%d\n", ans/2);
}
int Fi(int x) {
return fa[x] == x? x: fa[x] = Fi(fa[x]);
}
int get(int x, int y) {
uLL tmp = x;
tmp = tmp * base * base + y * base + x ^ y;
if(mp[tmp]) return mp[tmp];
mp[tmp] = ++n;
return n;
}
int main(int argc, char const *argv[]) {
while(~scanf("%d%d", &n, &m)) {
memset(head, -1, sizeof(head));
tot = -1;
mp.clear();
tn = n;
for(int i = 1; i <= n; ++i) fa[i] = i;
for(int i = 0, u, v, c, pa, pb, uc, vc; i < m; ++i) {
scanf("%d%d%d", &u, &v, &c);
pa = Fi(u), pb = Fi(v);
fa[pa] = pb;
uc = get(u, c); vc = get(v, c);
add_edge(u,uc,1);add_edge(uc,vc,0);add_edge(vc,v,1);
add_edge(v,vc,1);add_edge(vc,uc,0);add_edge(uc,u,1);
}
if(Fi(tn) != Fi(1)){
printf("-1\n");
continue;
}
dij();
}
return 0;
}
TLE_code
#include <cstdio>
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define fi first
#define se second
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
const int INF = 0x3f3f3f3f;
const int MXN = 1e5 + 5;
const int MXT = 4e5 + 6;
int n, m;
int head[MXN], tot;
struct lp {
int v, c, nex;
}cw[MXT];
vector<pii> mp[MXN];
int dis[MXT], vis[MXT], fa[MXN];
void add_edge(int u,int v,int w) {
cw[++tot].v = v;cw[tot].c = w;cw[tot].nex = head[u];
head[u] = tot;
cw[++tot].v = u;cw[tot].c = w;cw[tot].nex = head[v];
head[v] = tot;
}
void dij() {
priority_queue<pii,vector<pii>,greater<pii> >Q;
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
for(int i = head[1]; ~i; i = cw[i].nex) {
dis[i] = 1;
Q.push({dis[i], i});
}
int ans = INF;
while(!Q.empty()) {
pii now = Q.top();Q.pop();
if(vis[now.se]) continue;
vis[now.se] = 1;
int u = now.se, a = cw[u].v;
if(a == n) {
ans = min(ans, dis[u]);
break;
}
for(int i = head[a]; ~i; i = cw[i].nex) {
if(vis[i]) continue;
if(dis[i]>dis[u]+(cw[i].c!=cw[u].c)) {
dis[i] = dis[u]+(cw[i].c!=cw[u].c);
Q.push({dis[i], i});
}
}
}
while(!Q.empty()) Q.pop();
if(ans == INF) ans = -1;
printf("%d\n", ans);
}
int Fi(int x) {
return fa[x] == x? x: fa[x] = Fi(fa[x]);
}
int main(int argc, char const *argv[]) {
while(~scanf("%d%d", &n, &m)) {
memset(head, -1, sizeof(head));
tot = -1;
for(int i = 1; i <= n; ++i) fa[i] = i;
for(int i = 0, u, v, c, pa, pb; i < m; ++i) {
scanf("%d%d%d", &u, &v, &c);
add_edge(u, v, c);
pa = Fi(u), pb = Fi(v);
fa[pa] = pb;
}
if(Fi(n) != Fi(1)){
printf("-1\n");
continue;
}
dij();
}
return 0;
}
Problem Description:
AtCoder ARC061E Snuke's Subway Trip 最短路的更多相关文章
- AtCoder arc061C Snuke's Subway Trip
大意: 给你一张无向图,边有种类. 当你第一次/重新进入某种边时费用 + 1 在同一种边之间行走无费用. 求 1 到 n 的最小费用. 嗯...乍一看有一个很直观的想法:记录每个点的最短路的上一条边的 ...
- ARC061E Snuke's Subway Trip
传送门 题目大意 已知某城市的地铁网由一些地铁线路构成,每一条地铁线路由某一个公司运营,该城市规定:若乘坐同一公司的地铁,从开始到换乘只需要一块钱,换乘其他公司的价格也是一块钱,问从1号地铁站到n号地 ...
- 【例题收藏】◇例题·I◇ Snuke's Subway Trip
◇例题·I◇ Snuke's Subway Trip 题目来源:Atcoder Regular 061 E题(beta版) +传送门+ 一.解析 (1)最短路实现 由于在同一家公司的铁路上移动是不花费 ...
- Snuke's Subway Trip
すぬけ君の地下鉄旅行 / Snuke's Subway Trip Time limit : 3sec / Memory limit : 256MB Score : 600 points Problem ...
- 2018.09.19 atcoder Snuke's Subway Trip(最短路)
传送门 就是一个另类最短路啊. 利用颜色判断当前节点的最小花费的前驱边中有没有跟当前的边颜色相同的. 如果有这条边费用为0,否则费用为1. 这样跑出来就能ac了. 代码: #include<bi ...
- [ARC061E]すぬけ君の地下鉄旅行 / Snuke's Subway Trip
题目大意:Snuke的城镇有地铁行驶,地铁线路图包括$N$个站点和$M$个地铁线.站点被从$1$到$N$的整数所标记,每条线路被一个公司所拥有,并且每个公司用彼此不同的整数来表示. 第$i$条线路($ ...
- POJ 2502 Subway (最短路)
Subway 题目链接: http://acm.hust.edu.cn/vjudge/contest/122685#problem/L Description You have just moved ...
- POJ2502:Subway(最短路)
Subway Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 14634 Accepted: 4718 题目链接:http ...
- atcoder C - Snuke and Spells(模拟+思维)
题目链接:http://agc017.contest.atcoder.jp/tasks/agc017_c 题解:就是简单的模拟一下就行.看一下代码就能理解 #include <iostream& ...
随机推荐
- 模拟+双指针——cf1244E
排一遍序然后用l,r指针进行移动,每次移动的是靠1,或靠n更近的那个指针 #include<bits/stdc++.h> using namespace std; typedef long ...
- 出现Warning: date(): It is not safe to rely on the system's timezone settings的解决办法
在没有配置,尤其是新安装的PHP中使用date函数时,会报这个错误: Warning: date(): It is not safe to rely on the system's timezone ...
- B/S 和 C/S 架构软件
1.B/S架构: 通过C语言或java可以实现,使用B/S架构的软件,启动.打开应用和原生软件一样的效果. (正常浏览器打开的应用页面是有地址栏.菜单栏和标签栏的,但是通过配置可以关闭这些窗口,使B/ ...
- Sqli labs系列-less-1 详细篇
要说 SQL 注入学习,网上众多的靶场,就属 Sqli labs 这个系列挺不错的,关卡达到60多关了,我自己也就打了不几关,一个挺不错的练习SQL注入的源码. 我一开始就准备等我一些原理篇总结完了, ...
- js委托事件-addEventListeners(冒泡方向)
JQuery中live().delegate().on()事件都能给新增元素绑定事件,原理就是用了事件委托. 实例: 给id为div的元素绑定一个click委托,如果冒泡上来的元素是P元素就会执行al ...
- 浅谈学习selenium的一些知识点的总结
学习自动化测试,先得学习一门语言.自动化对语言要求掌握的程度不深,但必须得会基本的入门语法. 我学习的是python2,简单,易懂,上手快. 每天敲就是了. 我的学习路径是: 先学习一段时间pytho ...
- 4种XML解析器
<?xml version="1.0" encoding="UTF-8"?> <Result> <VALUE> <NO ...
- python re 正則匹配規則
- linux进阶之路(三):vi/vim编辑器
所有Linux都会内置vi,vim是vi的增强版本,被誉为"编辑之神",玩转vim可以让你完全脱离鼠标. vim可以分为两种模式: 普通模式:使用vim 文件名,进入普通模式.普通 ...
- 4.2.1 Vector bit-select and part-select addressing
Frm:IEEE Std 1364™-2001, IEEE Standard Verilog® Hardware Description Language Bit-selects extract a ...