[计算几何+图论]doge

题意

在平面直角坐标系上，你有一只doge在原点处。doge被绳子拴住了，绳子不会打结，没有弹性（但很柔软），并且长度为L。平面上有一些目标，因此你的doge会按照顺序去捡起它们，但是doge只能走直线。此外平面上还有一些障碍，视为一些点，狗在绕圈时可能会把绳子缠在上面。问L的最小值。

坐标均为整数，所有数的绝对值都不超过1000。物品和障碍物数量和不超过100。

“缠绕”：

、

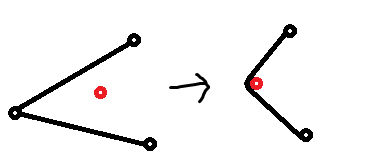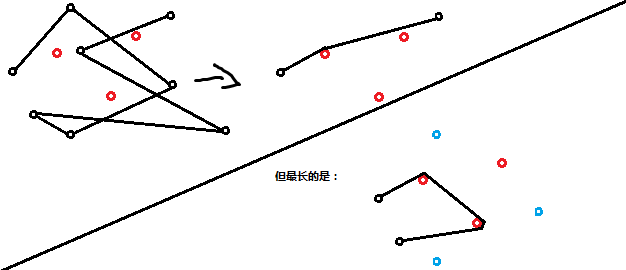
注意，虽然画的物品和障碍物是一个圈，但实际上可看做一个点。

---

思考

一些性质：

1.乱套模板是不可做的。

2.答案为doge依次捡起1~i物品中，绳子能缩短的最大值。因为doge可以沿这个能缩短的路径走，捡起一个物品后能回溯到原点。

3.doge在以此捡起1~i的物品中，doge一定会走最短路。因为这才更有可能使答案更优。

4.最短的路径是不能乱走的，但仿佛与两点与线段的位置有关。

先将所有点旋转一个角度，使得他们都不在同一条与x轴垂直的线上。

红线是doge可能走的路径。而这个答案为所有红线绷紧后的长度。

而此时对于有经过顺序的红线，它是否弯折，怎么弯折，只跟它现在经过某个障碍物上下面的顺序有关（图中的上下是黑色圈的上部分线段和下部分线段）。对于一个经过上下顺序相同的线段，可看做它们是等价的（虽然长度可能不同）。也就是说，若一种红线经过上下顺序已经给定，它长度的最小值就是（所有（有这种顺序的）（红线的）（长度的））最小值。

这个顺序我们可以表示成一个类似于括号序列的东西。如上图，红线必须经过的顺序为1^-2^-3^-4^-4⁺3⁺2⁺1⁺，代表了它依次经过了哪个障碍，上面还是下面。

先假我们已经会求出一个序列的答案。

5.若某次新添加一个物品后，序列最后中出现x⁺x⁺或x^-x^-，可将其直接删去（即倒数第二个和最后一个）。

如图：

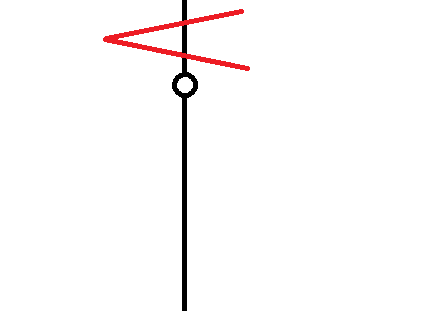
由于1⁺已经在上一次中得到了走到左边的答案，又因为这一次走到了右边，所以不会受到它的影响。

6.红线的序列为一些线段的序列拼接而成。并且线段的头尾一定在障碍物或原点或终点处。

直观的想，头尾代表了一个转折点，而转折点缩紧后一定会靠着障碍物。当然也可以三角形不等式说明。

有了这些性质，我们就可以根据序列建一张图。其中每条边代表了从一个障碍物（或起点）走到另一个障碍物（或终点）所需的长度，它能在图中当且仅当这条线段以此经过障碍物的上下顺序能匹配相应位置红线的序列。从起到向终点跑最短路，即为答案。

说了这么多，其实还是要多想。

---

代码

 #include<bits/stdc++.h>
 using namespace std;
 const double eps=1E-;
 const double pi=acos(-);
 const double INF=INT_MAX;
 const int maxn=1E2+;
 int q,n,m,top;
 double ans,f[];
 bool vis[maxn];
 int size,head[];
 struct pt
 {
     double x,y;
     pt(double a=,double b=)
     {
         x=a,y=b;
     }
     void operator=(pt A)
     {
         x=A.x,y=A.y;
     }
     double operator*(pt A)
     {
         return x*A.y-y*A.x;
     }
     pt operator-(pt A)
     {
         return pt(x-A.x,y-A.y);
     }
 }target[maxn],barrier[maxn];
 struct inf
 {
     int id,x;
     inf(int a=,int b=)
     {
         id=a,x=b;
     }
 }S[];
 struct edge
 {
     int to,next;
     double w;
 }E[];
 //////////////////////////////////////////////////////////////////
 //polygon
 //////////////////////////////////////////////////////////////////
 bool cmp(pt A,pt B)
 {
     return A.x<B.x;
 }
 pt rotate(pt A,double ra)
 {
     return pt(A.x*cos(ra)-A.y*sin(ra),A.x*sin(ra)+A.y*cos(ra));
 }
 int face(pt A,pt B,pt C)
 {
     double y=(B.y-A.y)/(B.x-A.x)*(C.x-A.x);
     if(A.y+y>=C.y)
         return ;
     return -;
 }
 bool inside(pt A,pt B,pt C)
 {
     return min(A.x,B.x)<=C.x&&C.x<=max(A.x,B.x);
 }
 double dis(pt A,pt B)
 {
     return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));
 }
 int cross(pt A,pt B)
 {
     double d=A*B;
     if(d>eps)
         return ;
     else
         return -;
 }
 void push(inf A)
 {
     if(A.id==S[top].id&&A.x==S[top].x)
         --top;
     else
         S[++top]=A;
 }
 //////////////////////////////////////////////////////////////////
 //polygon
 //////////////////////////////////////////////////////////////////

 //////////////////////////////////////////////////////////////////
 //graph
 //////////////////////////////////////////////////////////////////
 void add(int u,int v,double w)
 {
     E[++size].to=v;
     E[size].next=head[u];
     E[size].w=w;
     head[u]=size;
 }
 void clear()
 {
     for(int i=;i<=top+;++i)
         head[i]=;
     size=;
 }
 double spfa()
 {
     for(int i=;i<=top;++i)
         f[i]=INF;
     f[]=;
     vis[]=;
     queue<int>Q;
     Q.push();
     while(!Q.empty())
     {
         int u=Q.front();
         vis[u]=;
         Q.pop();
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             double nw=E[i].w+f[u];
             if(nw<f[v])
             {
                 f[v]=nw;
                 if(!vis[v])
                 {
                     vis[v]=;
                     Q.push(v);
                 }
             }
         }
     }
     return f[top--];
 }
 bool check(int l,int r)
 {
     for(int i=l+;i<=r-;++i)
         if(face(barrier[S[l].id],barrier[S[r].id],barrier[S[i].id])!=S[i].x)
             return false;
     return true;
 }
 double get(int x)
 {
     clear();
     barrier[n+m+]=target[x];
     push(inf(n+m+,));
     for(int i=;i<=top;++i)
         for(int j=i+;j<=top;++j)
             if(check(i,j))
                 add(i,j,dis(barrier[S[i].id],barrier[S[j].id]));
     for(int i=;i<=top;++i)
         if(check(,i))
             add(,i,dis(pt(,),barrier[S[i].id]));
     return spfa();
 }

 //////////////////////////////////////////////////////////////////
 //graph
 //////////////////////////////////////////////////////////////////

 void solve()
 {
     top=ans=;
     cin>>n>>m;
     for(int i=;i<=n;++i)
     {
         cin>>target[i].x>>target[i].y;
         target[i].x+=0.00001;
         target[i].y+=0.00001;
         target[i]=rotate(target[i],pi/);
     }
     for(int i=;i<=m;++i)
     {
         cin>>barrier[i].x>>barrier[i].y;
         barrier[i].x-=0.00001;
         barrier[i].y-=0.00001;
         barrier[i]=rotate(barrier[i],pi/);
     }
     sort(barrier+,barrier+m+,cmp);
     pt now(,);
     for(int i=;i<=n;++i)
     {
         if(target[i].x>now.x)
         {
             for(int j=;j<=m;++j)
                 if(inside(now,target[i],barrier[j]))
                     push(inf(j,face(now,target[i],barrier[j])));
         }
         else
         {
             for(int j=m;j>=;--j)
                 if(inside(now,target[i],barrier[j]))
                     push(inf(j,face(now,target[i],barrier[j])));
         }
         now=target[i];
         double g=get(i);
         ans=max(ans,g);
     }
     cout<<fixed<<setprecision()<<ans<<endl;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin>>q;
     while(q--)
         solve();
     return ;
 }
 /*
 2
 8  4
 2  -1
 3  0
 3  2
 0  1
 3  2
 3  0
 2  -1
 0  0
 1  0
 2  0
 1  1
 2  1
 */

 /*
 5.00
 */

类似题：http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=1164。