ROC 曲线

Receiver Operating Characteristic (接收机操作特性曲线)

是以虚警率为横轴，以击中率为纵轴，长成如下模样：

所谓击中率（hit）是指将正样本判断为正样本的比例，而虚警率（false alarm）是指将负样本判断为正样本的比例。

对书中例子的解读：

假如我们要检测一个脉冲信号，检测器检测到的是内部某点的电压值，当外部脉冲信号出现时具有均值u1,不出现时具有均值u2.假设由于噪声的影响二者服从均值不同方差相同的两个正态分布，如下图：

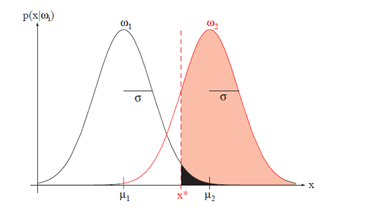
构造分类器，以x*为阈值，对一堆有标签（正，负）样本进行分类后，击中率是指分类器得到的正类中标签为正类的占所有标签为正类的比例，虚警率是指分类器得到的正类中标签原本为负类的占标签为负类的比例。不断地改变x*的值就能得到多个点这样就构成了第一幅图中的一条曲线。这条曲线上的点越靠近左上方，说明该点的击中率越高且同时虚警率低。

当我们改变u1,u2和sigma 时，分类器会随着改变，第一幅图中的d就是用来衡量这种改变的，，d的不同表示分类器不同，绘制出不同的曲线，当曲线下方面积越大时代表这个分类器越好。

这种方法通常用来评价对比几个不同的分类器的好坏。

参考书目：《Pattern Classification》Richard O.Duda 等:2.8.3 Signal Detection Theory and Operating Characteristics(P33-P35)；

链接：http://pan.baidu.com/s/1kVbB95t