OpenCASCADE圆与平面求交

OpenCASCADE圆与平面求交

eryar@163.com

在 解析几何求交之圆与二次曲面中分析了OpenCASCADE提供的类IntAna_IntConicQuad可以用来计算圆与二次曲面之间的交点，这个算法是将平面Plane作为二次曲面的一个特例来处理，最后主要是对三角函数方程进行求解。

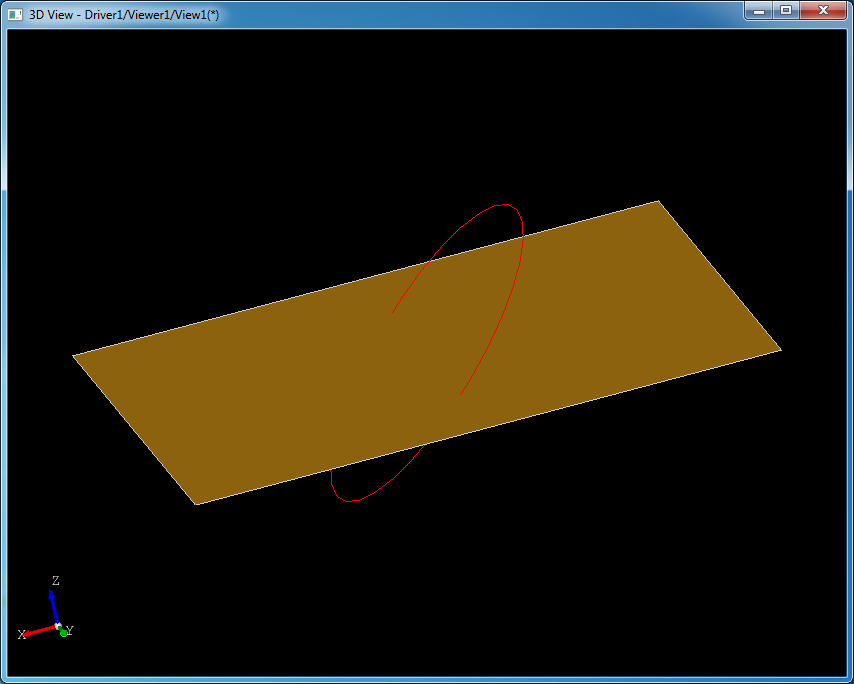
当直接使用圆和平面作为参数时，IntAna_IntConicQuad重载了函数Perform来对圆和平面进行求交计算，这时的算法与前面解三角函数不同，代码如下：

void IntAna_IntConicQuad::Perform (const gp_Circ& C, const gp_Pln& P,
				  const Standard_Real Tolang,
				  const Standard_Real Tol)
{

  done=Standard_False;

  gp_Pln Plconic(gp_Ax3(C.Position()));
  IntAna_QuadQuadGeo IntP(Plconic,P,Tolang,Tol);
  if (!IntP.IsDone()) {return;}
  if (IntP.TypeInter() == IntAna_Empty) {
    parallel=Standard_True;
    Standard_Real distmax = P.Distance(C.Location()) + C.Radius()*Tolang;
    if (distmax < Tol) {
      inquadric = Standard_True;
    }
    else {
      inquadric = Standard_False;
    }
    done=Standard_True;
  }
  else     if(IntP.TypeInter() == IntAna_Same) {
    inquadric = Standard_True;
    done = Standard_True;
  }
  else {
    inquadric=Standard_False;
    parallel=Standard_False;
    gp_Lin Ligsol(IntP.Line(1));

    gp_Vec V0(Plconic.Location(),Ligsol.Location());
    gp_Vec Axex(Plconic.Position().XDirection());
    gp_Vec Axey(Plconic.Position().YDirection());

    gp_Pnt2d Orig(Axex.Dot(V0),Axey.Dot(V0));
    gp_Vec2d Dire(Axex.Dot(Ligsol.Direction()),
		  Axey.Dot(Ligsol.Direction()));

    gp_Lin2d Ligs(Orig,Dire);
    gp_Pnt2d Pnt2dBid(0.0,0.0);
    gp_Dir2d Dir2dBid(1.0,0.0);
    gp_Ax2d Ax2dBid(Pnt2dBid,Dir2dBid);
    gp_Circ2d Cir(Ax2dBid,C.Radius());

    IntAna2d_AnaIntersection Int2d(Ligs,Cir);

    if (!Int2d.IsDone()) {return;}

    nbpts=Int2d.NbPoints();
    for (Standard_Integer i=1; i<=nbpts; i++) {

      gp_Pnt2d resul(Int2d.Point(i).Value());
      Standard_Real X= resul.X();
      Standard_Real Y= resul.Y();
      pnts[i-1].SetCoord(Plconic.Location().X() + X*Axex.X() + Y*Axey.X(),
			 Plconic.Location().Y() + X*Axex.Y() + Y*Axey.Y(),
			 Plconic.Location().Z() + X*Axex.Z() + Y*Axey.Z());
      paramonc[i-1]=Int2d.Point(i).ParamOnSecond();
    }
    done=Standard_True;
  }
}

　　

从上述代码中可以看出，直接对圆和平面求交的算法步骤如下：

l 对圆所在平面与平面进行求交，来判断圆所在平面与平面的状态：平行或是圆在平面内部；

l 如果圆所在平面与平面不平行，则得出交线；

l 然后将交线和圆转换成二维空间进行求交计算；

我觉得在得出圆所在平面与平面的交线后，再转换到二维空间来计算交点的方法有点复杂。在得到两个平面的交线后，就可以直接将圆心P0坐标向交线投影得到垂点Pm，先判断圆心到Pm点距离等于半径时，圆和平面就只有一个交点，就是Pm。小于半径时有两个交点，将Pm沿着交线方向分别移动L和－L距离就可以得到交点了，其中：

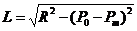
这样处理只涉及到一个点向直线投影、一个开方及几个向量操作，代码简单容量理解。