AcWing 3. 完全背包问题

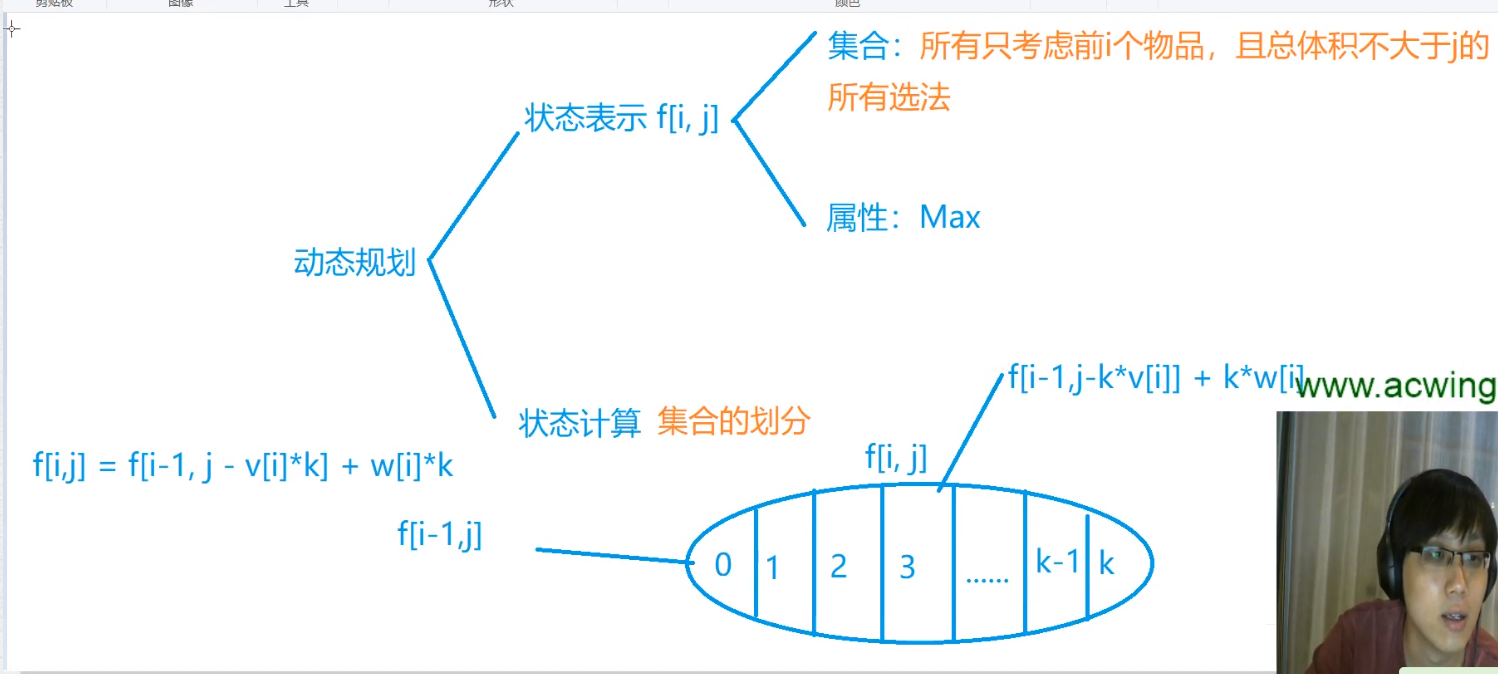
朴素

#include<iostream>
#include<algorithm>
using namespace std ;
const int N=;
int n,m;
int v[N],w[N];
int f[N][N];
int main() {
    cin>>n>>m;//n个物品 最大体积位m
    for(int i=; i<=n; i++) cin>>v[i]>>w[i];
    for(int i=; i<=n; i++)
        for(int j=; j<=m; j++)
            for(int k=; k*v[i]<=j; k++)//选k个第i个物品
                f[i][j]=max(f[i][j],f[i-][j-v[i]*k]+k*w[i]);
    cout<<f[n][m]<<endl;
    return ;
}

优化二维

//01背包从i-1转移过来   而完全背包是从第

i层转移过来
#include <iostream>
#include <algorithm>
using namespace std;
const int N = ;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
    cin >> n >> m;
    for (int i = ; i <= n; i ++ ) cin >> v[i] >> w[i];
    for (int i = ; i <= n; i ++ )
        for (int j = ; j <= m; j ++ )
            for(int k=; k*v[i]<=j; k++)
                f[i][j] = max(f[i][j], f[i-][j - v[i]*k] + w[i]*k);
    cout << f[n][m] << endl;
    return ;
}

终极一维

//一维
#include <iostream>
#include <algorithm>
using namespace std;
const int N = ;
int n, m;
int v[N], w[N];
int f[N];
int main() {
    cin >> n >> m;//n是数量,m是体积
    for (int i = ; i <= n; i ++ )
        cin >> v[i] >> w[i];
    for (int i = ; i <= n; i ++ )
        for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return ;
}