Java数据结构和算法(八)--红黑树与2-3树

红黑树规则：

　　1、每个节点要么是红色，要么是黑色

　　2、根节点都是黑色节点

　　3、每个叶节点是黑色节点

　　3、每个红色节点的两个子节点都是黑色节点，反之，不做要求，换句话说就是不能有连续两个红色节点

　　4、从任意节点到所有叶子节点上的黑色节点数量是相同的

　　一般对红黑树的讲述都是先给出这样的定义，这样想对不太容易理解的，而在算法4一书中，直接跳过这些规则，而讲述了红黑树与2-3树的等价性。如果我们先了解2-3树，理解了红黑树与2-3树之间的关系，再来看这些规则，就容易理解了

2-3树：

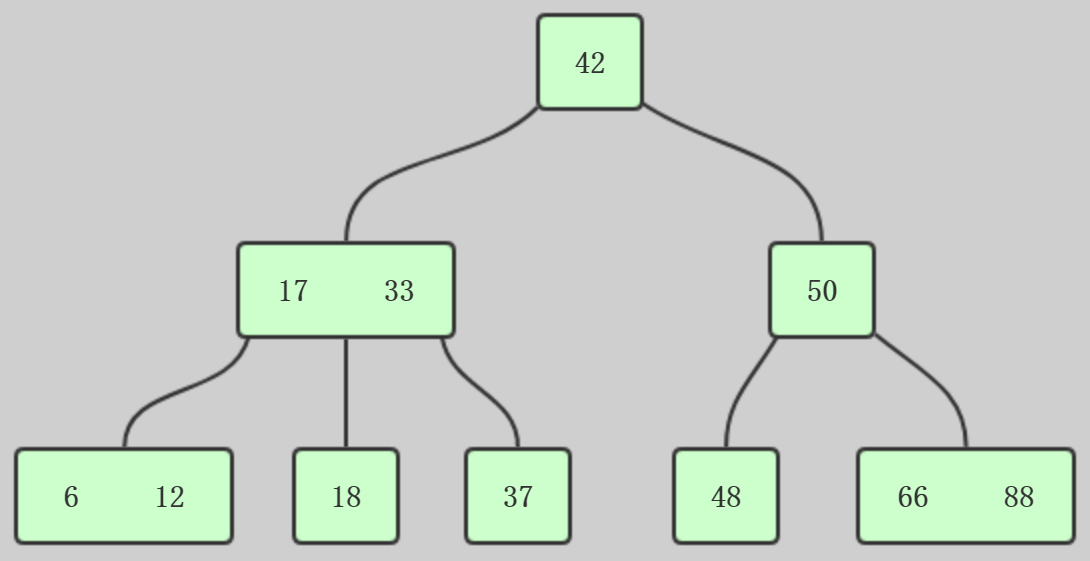
2-3树满足二分搜索树的基本性质，但是不是二叉树

2-3树节点可以存放一个元素或两个元素，每个节点有两个(2节点)或三个子节点(3节点)，这就是2-3树

2-3树是一个绝对平衡的树

2-3树的绝对平衡性：

1、2-3树新插入的节点一定不能插到空节点的位置

2、如果一个新节点插入到2节点，就会形成3节点

3、如果一个心机诶单插入到3节点，临时形成4节点，然后进行变形

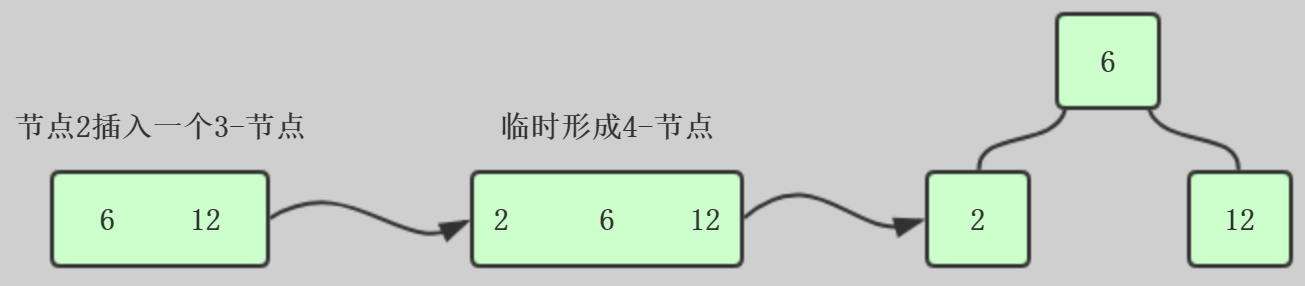
如果这个节点是根节点，这样就处理完了，如果插入的节点是叶子节点

1).父节点为2-节点

2).父节点为3-节点

通过上面的规则，实现了2-3树的绝对平衡

红黑树和2-3树的等价性：

将2节点与3节点类比到红黑树

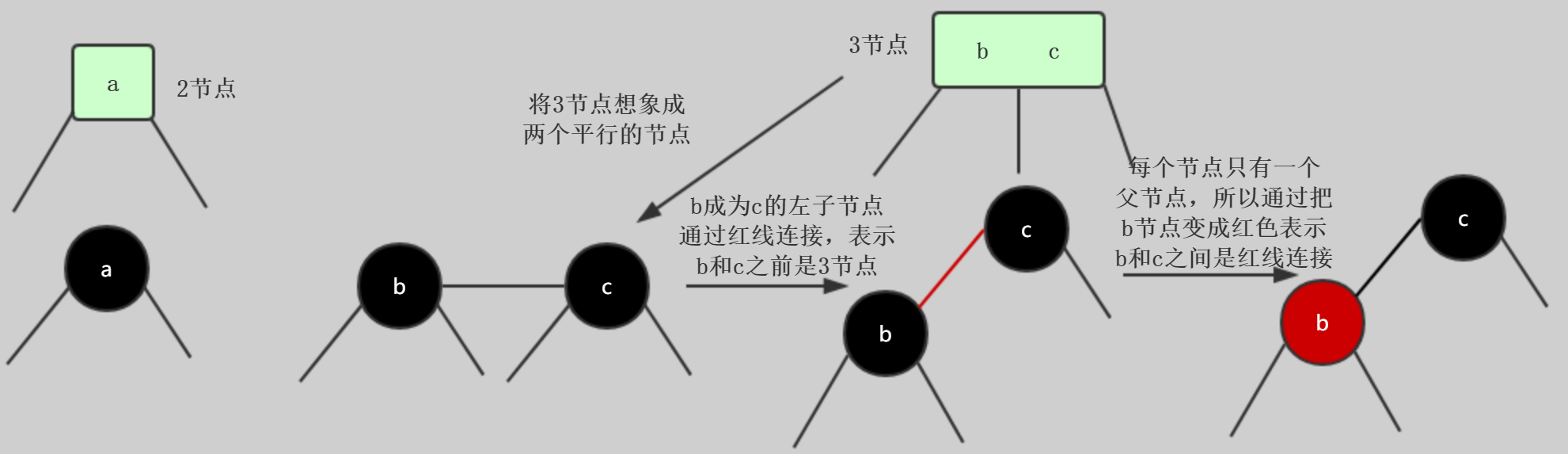
通过上面的过程，我们得到红黑树，所有红色节点都是左倾斜

实践：

　　所以此时我们很容易就能把2-3树转换为红黑树

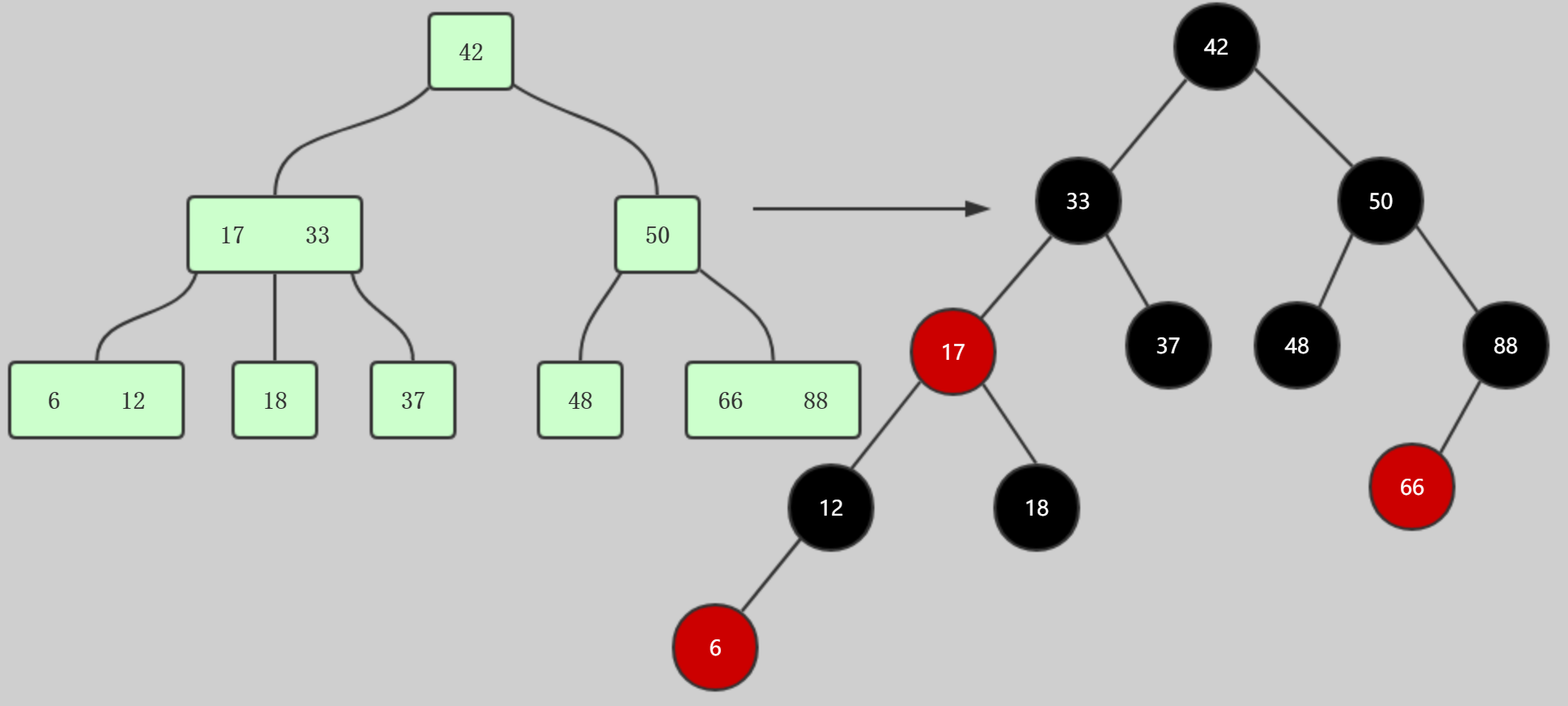
原来的2-3树有三个3-节点，所以红黑树中就有三个红色节点

通过2-3树理解红黑树的几个特征

特征：

1、每个节点要么是红色，要么是黑色

2、根节点是黑色节点

　　根节点肯定是黑色的，因为在2-3树中，根节点要么是2节点，要么是3节点，对应红黑树根节点肯定是黑色的

3、每个叶子节点(最后的空节点，而不是左右子树都为空的节点)是黑色节点

　　这里叶子节点是指这个节点为空，不是左右子树都为空的节点，包含空树的情况

　　if(node == null)
　　　　return BLACK;

4、每个红色节点的两个子节点都是黑色节点，反之，不做要求，换句话说就是不能有连续两个红色节点

　　红色节点对应2-3树中的3节点，红节点的两个子节点对应3节点的左子节点和中间节点，这两个节点无论是2节点还是3节点，首先连接的肯定是黑色的，例如这里的17节点

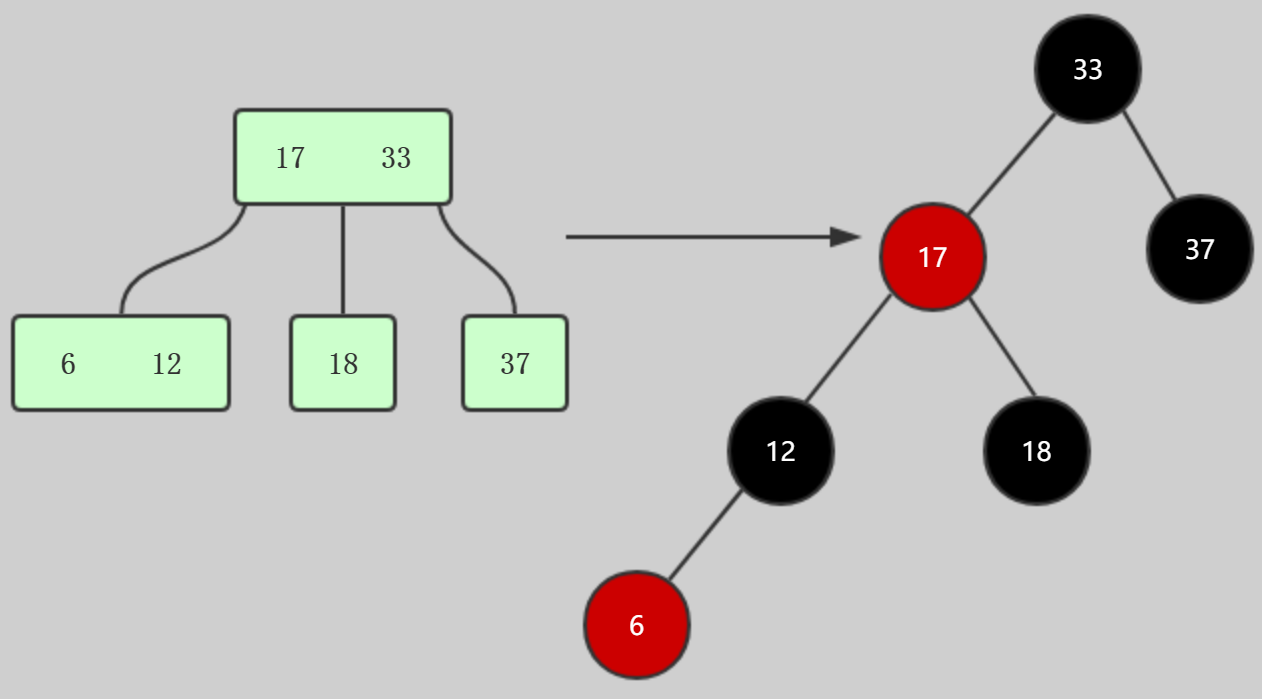
　　这里也可以看出来，黑色节点的右子节点肯定是黑色的，这个算是延伸内容

5、从任意节点到所有叶子节点上的黑色节点数量是相同的

　　这里类比到2-3树中，任意一个节点到叶子节点的经过的节点都是相同的，因为2-3是绝对平衡的树

　　从2-3树类比过来，任意一个节点到叶子节点经过的节点，无论是2节点还是3节点，肯定包含一个黑色的节点，但是红色不一定的，所以才有了第五条规则/特性

　　我们解释完了这五条特性，通过2-3树去理解，相比直接去死记硬背，简单很多

PS：红黑树是保持"黑色平衡"的二叉树，严格来说，不是平衡二叉树，最大高度：2logn，O(longn)

如果只是查询，AVL树的效率更高，如果删除和修改，红黑树更适合

Node定义：新添加节点默认红色

public class RBTree<K extends Comparable<K>, V> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private class Node {
        public K key;
        public V value;
        public Node left, right;
        public boolean color;

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            //这里默认添加节点为红色，因为在2-3树新增加一个节点总是要和叶子节点融合的，这里不论后序操作，
            //对应红黑树中一个红色节点和黑色节点
            color = RED;
        }
    }
}

左旋：

//   node                     x
//  /   \     左旋转         /  \
// T1   x   --------->   node   T3
//     / \              /   \
//    T2 T3            T1   T2
private Node leftRotate(Node node){

	Node x = node.right;

	// 左旋转
	node.right = x.left;
	x.left = node;

	x.color = node.color;
	node.color = RED;

	return x;
}

　　红黑树的左旋和前面讲的AVL树左旋是相同的，只是有关于颜色的变化，想象2-3树添加场景，一个新节点添加到2节点，变成3节点

PS：这里不维护颜色的正确，只是左旋，颜色的维护在add()

颜色反转：往3节点添加一个更大的值，66添加到37-42

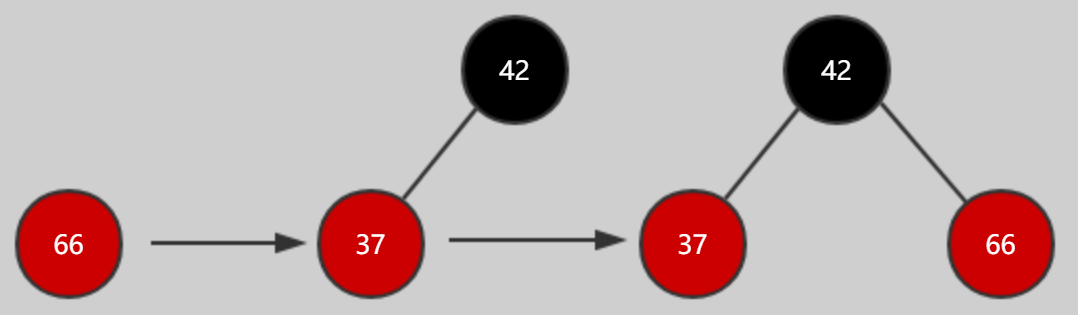
现在把节点66添加进来，对于二叉搜索树来说，会形成上面的结构

这样对于2-3树的场景：往3节点添加元素

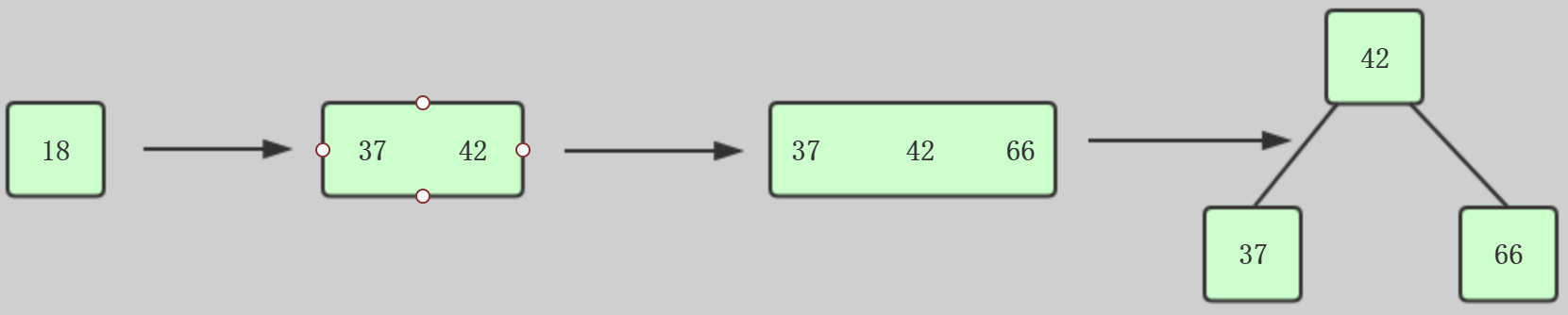
这时候，节点42需要向上融合，所以42应该是红色的，所以需要把节点42设置为红色

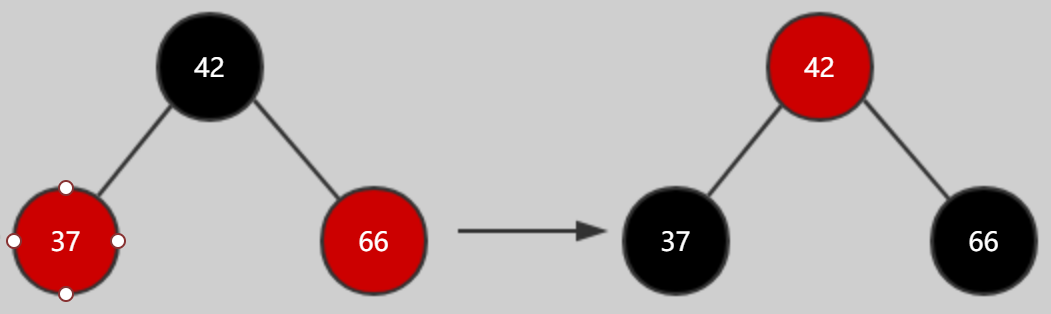
而红黑树的规则是：节点为红色，其两个子节点肯定是黑色的，所以有了上面的转变，也叫做颜色翻转，flipColors

//颜色翻转
private Node flipColors(Node node) {
	node.color = RED;
	node.left.color = BLACK;
	node.right.color = BLACK;
	return node;
}

右旋：往3节点添加一个更小的值，26添加到37-42

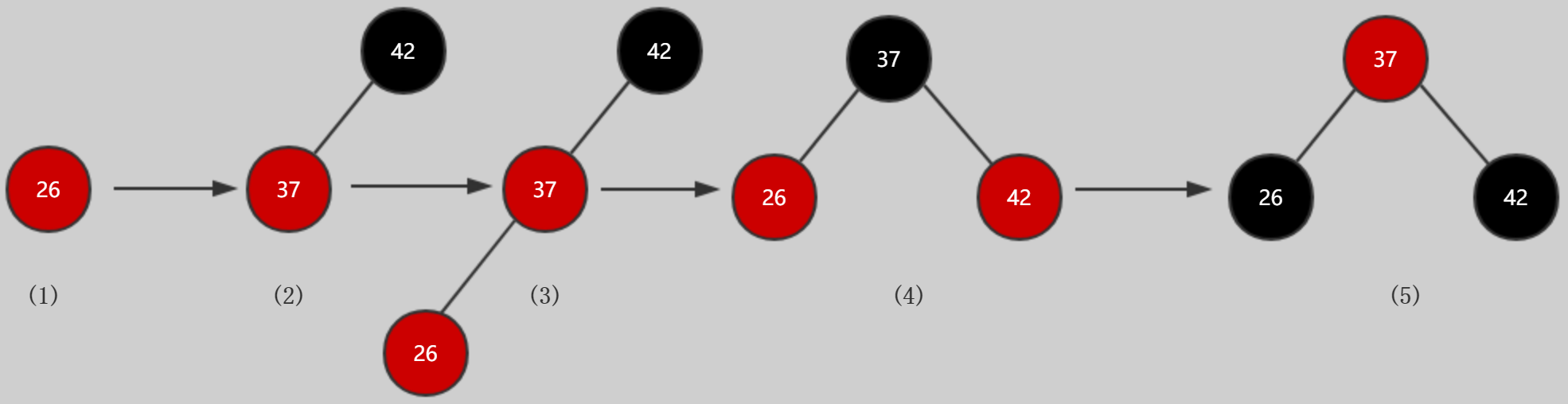
　　这种情况，自行对比2-3树场景，从(3)右旋，37的颜色要等于之前42的颜色为黑色，为了表示他们三个之前是一个4节点，所以42节点要变成

红色，右旋结束，然后进行颜色反转

//     node                   x
//    /   \     右旋转       /  \
//   x    T2   ------->   y   node
//  / \                       /  \
// y  T1                     T1  T2
private Node rightRotate(Node node){

	Node x = node.left;

	// 右旋转
	node.left = x.right;
	x.right = node;

	x.color = node.color;
	node.color = RED;   //因为这种情况相当于形成4节点，所以需要设置为红色

	return x;
}

我们上面讲述了左旋、右旋、颜色反转，分别对应着2-3树中：2节点添加、3节点添加更大的数据，3节点添加更小的值

如果往3节点添加一个中间值：例如40添加到37-42

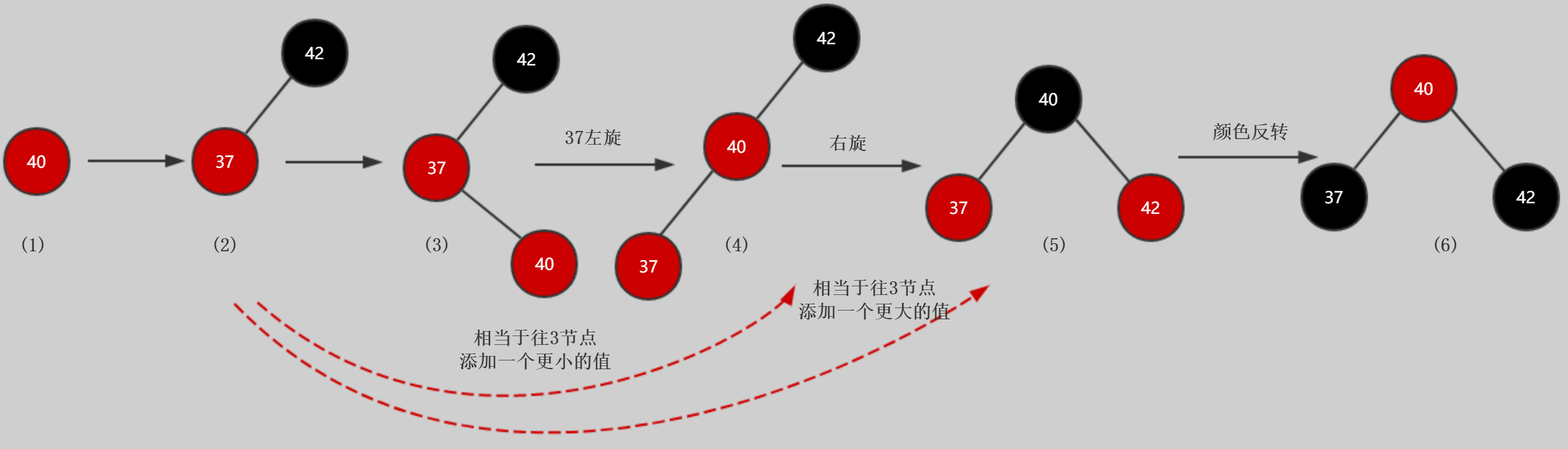
这种情况相当于：左旋+右旋+颜色反转，是最复杂的添加场景

可以包含上面讲的所有场景了，参考虚线描述，只是省略部分步骤，同样适用添加到2节点

红黑树添加元素：

// 向以node为根的红黑树中插入元素(key, value)，递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){

	if(node == null){
		size ++;
		return new Node(key, value); // 默认插入红色节点
	}

	if(key.compareTo(node.key) < 0)
		node.left = add(node.left, key, value);
	else if(key.compareTo(node.key) > 0)
		node.right = add(node.right, key, value);
	else // key.compareTo(node.key) == 0
		node.value = value;

	if (isRed(node.right) && !isRed(node.left))　　//右子节点为红色，左子节点为黑色
		node = leftRotate(node);

	if (isRed(node.left) && isRed(node.left.left))　　//左子节点为红色，左子节点的左子节点为红色
		node = rightRotate(node);

	if (isRed(node.left) && isRed(node.right))　　//左右子节点都是红色，惊醒颜色反转
		flipColors(node);

	return node;
}

左旋、右旋、颜色反转，这个顺序对应着上面的图

完整的RBTree.java代码：

public class RBTree<K extends Comparable<K>, V> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private class Node{
        public K key;
        public V value;
        public Node left, right;
        public boolean color;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            color = RED;
        }
    }

    private Node root;
    private int size;

    public RBTree(){
        root = null;
        size = 0;
    }

    public int getSize(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 判断节点node的颜色
    private boolean isRed(Node node){
        if(node == null)
            return BLACK;
        return node.color;
    }

    //   node                     x
    //  /   \     左旋转         /  \
    // T1   x   --------->   node   T3
    //     / \              /   \
    //    T2 T3            T1   T2
    private Node leftRotate(Node node){

        Node x = node.right;

        // 左旋转
        node.right = x.left;
        x.left = node;

        x.color = node.color;
        node.color = RED;

        return x;
    }

    //     node                   x
    //    /   \     右旋转       /  \
    //   x    T2   ------->   y   node
    //  / \                       /  \
    // y  T1                     T1  T2
    private Node rightRotate(Node node){

        Node x = node.left;

        // 右旋转
        node.left = x.right;
        x.right = node;

        x.color = node.color;
        node.color = RED;

        return x;
    }

    // 颜色翻转
    private void flipColors(Node node){

        node.color = RED;
        node.left.color = BLACK;
        node.right.color = BLACK;
    }

    // 向红黑树中添加新的元素(key, value)
    public void add(K key, V value){
        root = add(root, key, value);
        root.color = BLACK; // 最终根节点为黑色节点
    }

    // 向以node为根的红黑树中插入元素(key, value)，递归算法
    // 返回插入新节点后红黑树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value); // 默认插入红色节点
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else // key.compareTo(node.key) == 0
            node.value = value;

        if (isRed(node.right) && !isRed(node.left))
            node = leftRotate(node);

        if (isRed(node.left) && isRed(node.left.left))
            node = rightRotate(node);

        if (isRed(node.left) && isRed(node.right))
            flipColors(node);

        return node;
    }

    // 返回以node为根节点的二分搜索树中，key所在的节点
    private Node getNode(Node node, K key){

        if(node == null)
            return null;

        if(key.equals(node.key))
            return node;
        else if(key.compareTo(node.key) < 0)
            return getNode(node.left, key);
        else // if(key.compareTo(node.key) > 0)
            return getNode(node.right, key);
    }

    public boolean contains(K key){
        return getNode(root, key) != null;
    }

    public V get(K key){

        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }

    public void set(K key, V newValue){
        Node node = getNode(root, key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist!");

        node.value = newValue;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

}

红黑树、AVL树、二分搜索树对比：

这里关于红黑树完整的代码，包含测试代码地址：https://github.com/huigelaile1234/Huige.git

一共有三个测试：测试二分搜索树、 AVL树、红黑树的效率

Main.java：具体代码在上面GitHub地址

把英文版傲慢与偏见写入list，测试

for (String word : words) {
	if (bst.contains(word))
		bst.set(word, bst.get(word) + 1);
	else
		bst.add(word, 1);
}

for(String word: words)
	bst.contains(word);

输出结果：
BST: 0.130161098 s
AVL: 0.124234987 s
rbTree: 0.11852221 s

BST: 0.137865554 s
AVL: 0.120124769 s
rbTree: 0.13707878 s

BST: 0.143397424 s
AVL: 0.153158411 s
rbTree: 0.146772639 s

测试代码运行三次，我们看到三者差距并不大

1、在数据量不大的情况下，并不是时间复杂度更低的数据结构，效率一定更高

2、set()、contains()、get()几乎都是查询，红黑树的优势在于添加和查询

Main2.java：

int n = 20000000;

Random random = new Random(n);
ArrayList<Integer> testData = new ArrayList<>(n);
for(int i = 0 ; i < n ; i ++)
	testData.add(random.nextInt(Integer.MAX_VALUE));

BST<Integer, Integer> bst = new BST<>();
for (Integer x: testData)
	bst.add(x, null);

生成两千万个随机数，添加到list，然后分别添加到二分搜索树、AVL树、红黑树

输出结果：
BST: 53.912429302 s
AVL: 52.037609212 s
RBTree: 50.485452955 s

这里可以看到RBTree想对来说添加效率想对更高一点，但是由于测试时间太长，就测试一次，可能准确性可能不够，大家可以自行测试一下

Main3.java：

int n = 20000000;

ArrayList<Integer> testData = new ArrayList<>(n);
for(int i = 0 ; i < n ; i ++)
	testData.add(i);

这里和第二个测试区别就是添加有序数据，我们知道二分搜索树对于有序、倒序插入，就会退化为链表，所以这里只测试AVL树和红黑树

输出结果：
AVL: 8.990460311 s
RBTree: 6.297460938 s

AVL: 8.462381117 s
RBTree: 8.074237092 s

AVL: 10.381852688 s
RBTree: 6.812257725 s

总结：

　　1、对于随机数据，二分搜索树很好用，但是有序数据，会退化成链表，处于高度不平衡状态

　　2、AVL树是完全平衡的，适合查询的场景，例如get()、set()、contains()

　　3、红黑树不是平衡二叉树，统计性能更优(综合CURD操作)，适合add()、del()