TZOJ 3042 切蛋糕(并查集)

描述

KK是个心灵手巧的好姑娘，她做了一个大蛋糕请她的好朋友们来品尝。
这个蛋糕分成n×n个正方形小格，每个小格包含一块水果。KK要把蛋糕切成若干块，显然她不会破坏任意一个小格。
无聊的某同学在她切蛋糕时不停地问她同一种问题：某两个小格是否还在同一块蛋糕里？
例如下图中，KK从(1,1)切到(4,1)，又从(1,1)切到(1,4)，从而将蛋糕分成了两块。然后又从(2,1)切到(2,3)，从(1,3)切到(2,3)，于是把整个蛋糕分成了三块。其中小格(2,2)只和小格(2,3)连通，与其它所有小格不连通。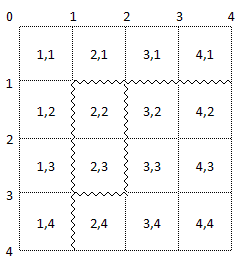

KK被这些无聊的问题烦透了，她请求你编写一个程序让他闭嘴。

输入

输入包括多组数据。
每组数据第一行为两个整数：蛋糕大小n (1≤n≤1000)，以及KK切蛋糕次数和问题数之和q (1≤q≤100000)
然后q行，每行是下面两者之一，描述了切蛋糕和问问题的过程：

• cut x1 y1 x2 y2
  沿着坐标(x1,y1)和(x2,y2)连成的直线段切割蛋糕。
  输入数据确保x1=x2和y1=y2恰有其一成立，坐标(x1,y1)和(x2,y2)连成的直线段一定在蛋糕内部，并且KK不会重复切同一位置。
• query x1 y1 x2 y2
  询问格子(x1,y1)和(x2,y2)是否在同一块蛋糕上(1≤x1, y1, x2, y2≤n)

输入数据以n=q=0结束。

输出

对于输入数据中的query问题，如果两个格子在同一块蛋糕上则输出”Yes”，否则输出”No”。

样例输入

4 11
query 1 1 2 2
cut 1 1 4 1
cut 1 1 1 4
query 1 1 2 2
query 2 2 3 3
cut 2 3 2 1
query 2 2 3 3
cut 1 3 2 3
query 2 2 3 3
query 2 2 2 3
query 1 1 2 4
1000 1
query 1 1 1000 1000
0 0

样例输出

Yes
No
Yes
Yes
No
Yes
No
Yes

题意

每次切一条线段，查询两块蛋糕是否被切开。

题解

相当于相邻蛋糕用边相连，然后删除一些边，询问是否连通。

只有删边操作，那么可以考虑并查集，因为并查集是加边操作，所以可以把问题倒过来。

每次加入并查集一条最后删掉的边。

并查集路径压缩和按秩合并均摊O(1)。

总时间复杂度O(n^2+q)。

代码

 #include<bits/stdc++.h>
 using namespace std;

 const int N=1e6+;
 const int M=1e5+;
 int f[N],d[N];
 bool g[][][],ans[M];
 int dx[]={,};
 int dy[]={,};
 int n;
 struct node
 {
     bool f;int x1,y1,x2,y2;
 }q[M];
 void init(int n)
 {
     for(int i=;i<=n;i++)for(int j=;j<=n;j++)for(int k=;k<;k++)g[i][j][k]=;
     int n1=n*n;for(int i=;i<=n1;i++)d[i]=,f[i]=i;
 }
 int F(int x){return f[x]==x?x:F(f[x]);}
 void merge(int x1,int y1,int x2,int y2)
 {
     int x=(x1-)*n+y1,y=(x2-)*n+y2;
     x=F(x),y=F(y);
     if(x==y)return;
     if(d[x]==d[y])d[x]++;
     if(d[x]<d[y])swap(x,y);
     f[y]=x;
 }
 int main()
 {
     int Q;char s[];
     while(scanf("%d%d",&n,&Q)!=EOF,n||Q)
     {
         init(n);
         for(int i=;i<=Q;i++)
         {
             scanf("%s%d%d%d%d",s,&q[i].y1,&q[i].x1,&q[i].y2,&q[i].x2);
             if(s[]=='q')q[i].f=;
             else
             {
                 q[i].f=;
                 if(q[i].x1==q[i].x2)
                 {
                     if(q[i].x1==n)continue;
                     if(q[i].y1>q[i].y2)swap(q[i].y1,q[i].y2);
                     for(int j=q[i].y1+;j<=q[i].y2;j++)g[q[i].x1][j][]=;
                 }
                 else
                 {
                     if(q[i].y1==n)continue;
                     if(q[i].x1>q[i].x2)swap(q[i].x1,q[i].x2);
                     for(int j=q[i].x1+;j<=q[i].x2;j++)g[j][q[i].y1][]=;
                 }
             }
         }
         for(int i=;i<=n;i++)for(int j=;j<=n;j++)
         {
             for(int k=;k<;k++)
                 if(g[i][j][k]&&i+dx[k]<=n&&j+dy[k]<=n)
                     merge(i,j,i+dx[k],j+dy[k]);
         }
         for(int i=Q;i>=;i--)
         {
             if(q[i].f)//query
             {
                 if(F((q[i].x1-)*n+q[i].y1)==F((q[i].x2-)*n+q[i].y2))ans[i]=;
                 else ans[i]=;
             }
             else//cut
             {
                 if(q[i].x1==q[i].x2)
                 {
                     if(q[i].x1==n)continue;
                     for(int j=q[i].y1+;j<=q[i].y2;j++)
                         merge(q[i].x1,j,q[i].x1+,j);
                 }
                 else
                 {
                     if(q[i].y1==n)continue;
                     for(int j=q[i].x1+;j<=q[i].x2;j++)
                         merge(j,q[i].y1,j,q[i].y1+);
                 }
             }
         }
         for(int i=;i<=Q;i++)if(q[i].f)printf("%s\n",ans[i]?"Yes":"No");
     }
     return ;
 }