Wannafly挑战赛13 zzf的好矩阵题解

文章目录

Wannafly挑战赛13 zzf的好矩阵题解

分析

结论1
结论2
结论3

C数组对应带子说明
空白长度论述
后续黑色长度论述
能“密铺”的带子形式及特征

最终结论

链接：https://ac.nowcoder.com/acm/contest/80/C

分析

每个格子都有至少一个麦穗
每个格子最多只能有p*p个麦穗
任意两个格子的麦穗数不同

结论1

由以上三点易得所有格子的麦穗数为p2p^2p2的全排列。

结论2

对于一个已知的一个符合题意的矩阵，行任意交换，列任意交换，或者所有行列进行转置，所得的矩阵仍然是一个符合条件的解。易得，如此一个基本解可以构造出2∗(p!)22*(p!)^22∗(p!)2个互不相同的解。

转置乘以2.行的顺序有p!p!p!种，列的顺序有p!p!p!种。

结论3

不考虑转置、行列交换等变换，本质不同的解有且只有一个。

以下主要是从不重不漏出发，逐步逼近，找到C(带子)需要满足的条件，最终确定可行的c与r.

用ri,cj,ai,jr_i,c_j,a_{i,j}ri,cj,ai,j分别表示第iii行选中的次数、第jjj列选中的次数，iii行jjj列的麦穗数。

ai,j=ri+cja_{i,j}=r_i+c_jai,j=ri+cj.

r=(r1,r2,r3,...,rp)r=(r_1,r_2,r_3,...,r_p)r=(r1,r2,r3,...,rp)

c=(c1,c2,c3,...,cp)c=(c_1,c_2,c_3,...,c_p)c=(c1,c2,c3,...,cp).

对于麦穗数为1的格子，显然只能分解成1+01+01+0或者0+10+10+1.

为了本质不同的解，我们不妨设行和列的选取数从小到大，且第一列取1，第一行取0.即：

r1<r2<r3<...<rp;c1<c2<c3<...<cp;c1=1, r1=0.r_1 \lt r_2 \lt r_3 \lt ... \lt r_p;\\
c_1 \lt c_2 \lt c_3 \lt ... \lt c_p; \\
c_1 = 1,\;r_1=0.r1<r2<r3<...<rp;c1<c2<c3<...<cp;c1=1,r1=0.

如此，确定一对r,cr,cr,c就确定了一个基本的解。

容易验证c=(1,2,3,4,...,p),r=(0,p,2p,3p,...,(p−1)p)c=\left(1,2,3,4,...,p\right), r=\left(0,p,2p,3p,...,(p-1)p\right)c=(1,2,3,4,...,p),r=(0,p,2p,3p,...,(p−1)p)是一个解。

接下来要说明只有这一组基本解。

C数组对应带子说明

空白长度论述

不断移动C数组锁画出的这条带子，注意需要满足以下两点要求：

1-p21\text{-}p^21-p2的中每一个格子都被黑色覆盖一次且仅一次（即不重不漏）。
rir_iri其实就是第iii次移动相比于初始位置的总的位移量。
为了不漏，移动之后，下一次带子的开头应对应于还没覆盖的第一个空白格子。

根据不重不漏，容易推出以下结论。

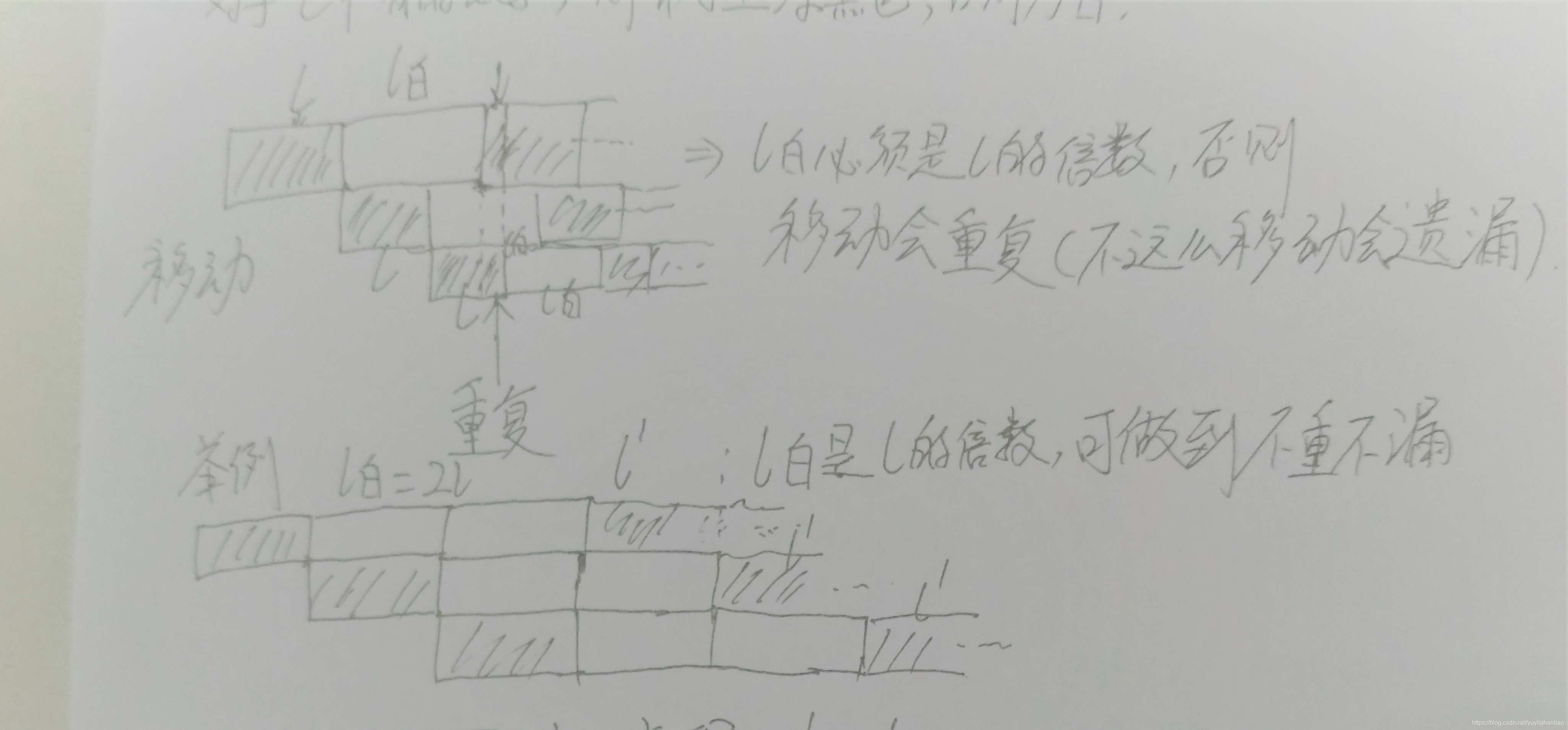
l白=kll_{白}=kll白=kl

后续黑色长度论述

l′=ll^{'}=ll′=l

并且用不重不漏容易推出如果后面还有白色段，则长度一定和前面的白色段等长，再有黑色段，则又和最开始的黑色段等长……

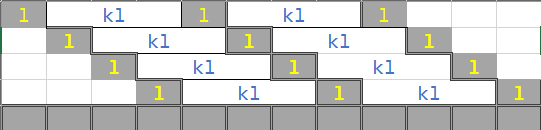
能“密铺”的带子形式及特征

其中l黑=l,l白=kll_{黑}=l,l_{白}=kll黑=l,l白=kl

共有k1k_1k1个kl白+l黑片段。

带子移动k次，加上原本的不移动的一条，则刚好不重不漏的“密铺”了连续的一段。之后只需要按照前面的整体右移即可。

下图是k=3的例子：

带子黑色总长度：

p=(k1+1)lp=(k_1+1)lp=(k1+1)l

“密铺”一段长度：

l+k1(kl+l)+kl=k1kl+(k+k1+1)ll+k_1(kl+l)+kl=k_1kl+(k+k_1+1)ll+k1(kl+l)+kl=k1kl+(k+k1+1)l

由于ppp是素数。

k1=0,l=pk_1 = 0,l=pk1=0,l=p,则带子只有第一块黑色的片段，长度为p，故c=(1,2,3,...,p)c=(1,2,3,...,p)c=(1,2,3,...,p),显然要密铺满1−p21-p^21−p2可得r=(0,p,2p,3p,...,(p−1)p)r=(0,p,2p,3p,...,(p-1)p)r=(0,p,2p,3p,...,(p−1)p).或者
k1=p−1,l=1k_1 = p-1,l=1k1=p−1,l=1,则带子有ppp块黑色的片段，每两个黑色片段之间有一块长度为kkk的白色片段。密铺总长度应该是p2p^2p2的因数。

p2=k2[k1kl+(k+k1+1)l]=k2[(p−1)k+(k+p)]=k2(k+1)p⇒p=k2(k+1)p^2=k_2\left[k_1kl+(k+k_1+1)l\right]\\=k_2\left[(p-1)k+(k+p)\right]\\=k_2(k+1)p \Rightarrow\\
p=k_2(k+1)p2=k2[k1kl+(k+k1+1)l]=k2[(p−1)k+(k+p)]=k2(k+1)p⇒p=k2(k+1)

故

2.a. k2=1,k=p−1k_2=1,k=p-1k2=1,k=p−1或

2.b. k2=p,k=0k_2=p,k=0k2=p,k=0

对于2.a可得c=(1,p+1,2p+1,...,(p−1)p+1),r=(0,1,2,3,4,...,p−1)c=(1,p+1,2p+1,...,(p-1)p+1), r=(0,1,2,3,4,...,p-1)c=(1,p+1,2p+1,...,(p−1)p+1),r=(0,1,2,3,4,...,p−1)

对于2.b可得c=(1,2,3,4,...,p),r=(0,p,2p,3p,...,(p−1)p)c=(1,2,3,4,...,p),r=(0,p,2p,3p,...,(p-1)p)c=(1,2,3,4,...,p),r=(0,p,2p,3p,...,(p−1)p)

综上1,2.a,2.b，

cα=(1,2,3,4,...,p), rα=(0,p,2p,3p,...,(p−1)p);cβ=(1,p+1,2p+1,...,(p−1)p+1), rβ=(0,1,2,3,4,...,p−1)c_{\alpha}=(1,2,3,4,...,p),\;r_{\alpha}=(0,p,2p,3p,...,(p-1)p);\\
c_{\beta}=(1,p+1,2p+1,...,(p-1)p+1),\; r_{\beta}=(0,1,2,3,4,...,p-1)cα=(1,2,3,4,...,p),rα=(0,p,2p,3p,...,(p−1)p);cβ=(1,p+1,2p+1,...,(p−1)p+1),rβ=(0,1,2,3,4,...,p−1)

但是，容易发现，∀i,j\forall i,j∀i,j,有

aα,i,j=rα,i+cα,j=[(i−1)p]+[j]=(i−1)p+j=aβ,j,i=rβ,j+cβ,i=[j−1]+[(i−1)p+1]=(i−1)p+ja_{\alpha,i,j}=r_{\alpha,i}+c_{\alpha,j}=[(i-1)p]+[j]=(i-1)p+j\\
=a_{\beta,j,i}=r_{\beta,j}+c_{\beta,i}=[j-1]+[(i-1)p+1]=(i-1)p+jaα,i,j=rα,i+cα,j=[(i−1)p]+[j]=(i−1)p+j=aβ,j,i=rβ,j+cβ,i=[j−1]+[(i−1)p+1]=(i−1)p+j

即α,β\alpha,\betaα,β这两种方案所得矩阵互为转置矩阵。所以应计算成一种基本解。

最终结论

因此，本质不同的解只有一种；考虑矩阵转置、行列交换等，一共有2∗(p!)22*(p!)^22∗(p!)2种解。