k-means学习笔记

最近看了吴恩达老师的机器学习教程（可以在Coursera，或者网易云课堂上找到）中讲解的k-means聚类算法，k-means是一种应用非常广泛的无监督学习算法，使用比较简单，但其背后的思想是EM算法（看李航老师统计学习方法看了半天还是没太明白，后面找了一篇博客，博主对EM算法讲解非常通俗易懂）。这里对k-means算法和应用做一个小笔记，脑袋记不住那么多hh。本文用的数据和代码见github.

一、k-means算法

在介绍k-means算法之前，先看一个课程中使用k-means对二维数据进行聚类的小例子。下图中（a）是原始样本点，在（b）图中随机选取两个点作为质心，即k-means中的k取2，然后计算各样本到质心的距离（一般用欧式距离），选择距离小的一个质心作为该样本的一个类，如（c）；之后再计算分好类的样本的中心点。重复以上过程可以看到效果如图（f）。

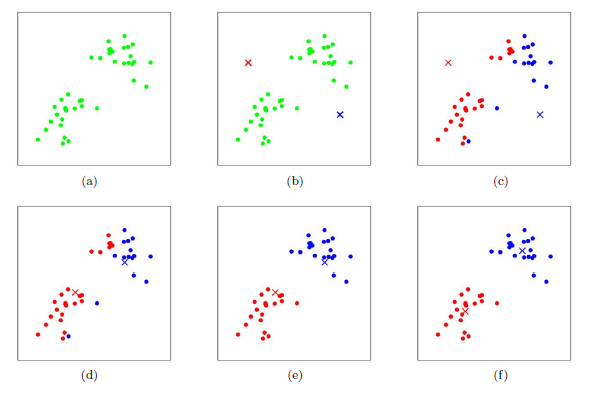
从上面的例子可以看出k-means的工作流程是首先随机选取k个初始点作为质心，然后将数据中的每个样本点按照距离分配到一个簇中，之后再计算各簇中样本点的中心，将其作为质心，然后重复以上过程。k-means算法如下：

将数据集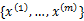分成k个簇。

1、 随机选取k个聚类质心点（cluster centroids）为。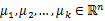

2、 重复下面过程直到收敛 {

               对于每一个样例i，计算其应该属于的类

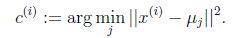               （1）

               对于每一个类j，重新计算该类的质心

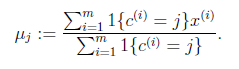               （2）

}

K是我们事先给定的聚类数，代表样例i与k个类中距离最近的那个类，的值是1到k中的一个。质心是属于同一个类的样本中心点。

k-means算法中要保证其是收敛的，定义损失函数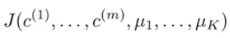如（3）式，表示每个样本点到其质心的平方和，k-means的优化目标是使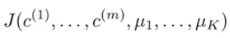最小化如（4）式。假设当前目标没有达到最小值，那么首先可以固定每个类的质心 ，调整每个样本的所属的类别  来让目标函数减少，同样，固定 ，调整每个类的质心  也可以使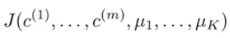减小。这两个过程就是算法中循环使目标单调递减的过程。当目标递减到最小时，和c也同时收敛。但（3）是非凸函数，所以k-means有可能不会达到全局最小值，而是收敛到局部最小值，这时我们可以多次随机选取质心初始值，然后对结果进行比较，选择使目标最小的聚类和质心。

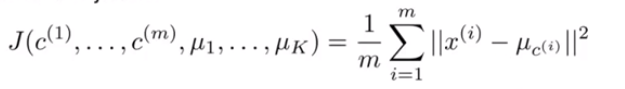（3）

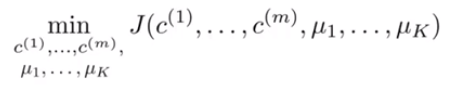            （4）

二、k的选择（仅供参考）

　　1、肘部法则

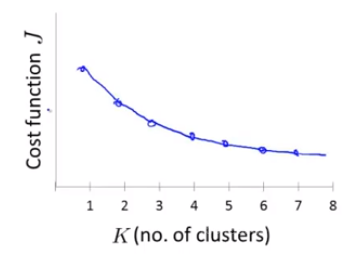
　　选择不同的k值，然后分别计算目标函数（4）式的值，然后画出目标函数值随聚类k的变化情况，如果图像如下图左边的图像所示，则选择拐点即k=3（拐点可以视为手的肘部，称为肘部法则 hh）。但是如果变化情况像右图一样，则没有出现明显的拐点，这时候肘部法则就不适用了（肘部法则不适用于所有情况）。

　　　　　　　　　　　　　　　　　　　　　

　　2、根据实际应用的目的选择K

　　可以根据聚类的目的选择相应的K值，比如T恤的大小与型号设置，如果选择k=3，则可以分为S/M/L三种型号，如果k=5，则可将T恤分为XS/S/M/L/XL。

三、k-means算法应用

课程中还留了k-means的练习，但里面是使用MATLAB/Octave编写的，一直用的python，这里就利用python来完成这个练习算了。该练习有两个题目，第一个题目是利用k-means对二维数据进行聚类，第二个题目是利用k-means对图片进行压缩。

1、第一题  二维数据聚类

第一步 数据存在ex7data2.mat文件中，这里先引入相关库，然后提取数据。

import pandas as pd
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

mat = loadmat('./ex7/ex7data2.mat')
print(mat)

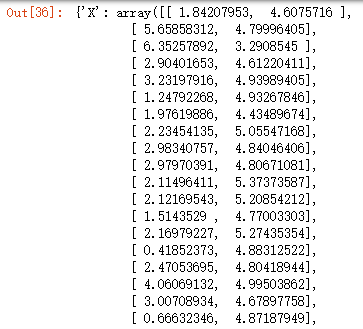
第二步 根据（1）式定义根据质心对样本聚类的函数findClosestCentroids。

def findClosestCentroids(Datas, centroids):  # Datas:array, centroids:array
    max_dist = np.inf  # 定义最大距离
    clustering = []  # 储存聚类结果
    # 遍历每个样本点
    for i in range(len(Datas)):
        data = Datas[i]
        diff = data - centroids   # 数据类型都为np.array
        dist = 0
        for j in range(len(diff[0])):
            dist += diff[:,j]**2   # 求欧式距离
        min_index = np.argmin(dist)  # 找出距离最小的下标
        clustering.append(min_index)
    return np.array(clustering)

X = mat['X']  # get data
centroids = np.array([[3,3], [6,2], [8,5]])
# 测试
clusted = findClosestCentroids(X, centroids)
clusted[:5]

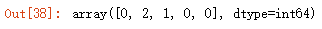
这里k取3，定义质心为[[3,3], [6,2], [8,5]]，对数据进行测试，对应的聚类为[0,2,1,0,0].

第三步 根据（2）式定义根据分类重新计算中心点的函数computMeans。

def computMeans(Datas, clustering):
    centroids = []
    for i in range(len(np.unique(clustering))):  # np.unique计算聚类个数
        u_k = np.mean(Datas[clustering==i], axis=0)  # 求每列的平均值
        centroids.append(u_k)
    return np.array(centroids)

用以上的聚类结果对其进行测验

centroids = computMeans(X, clusted)
centroids

第四步 定义展示最终聚类结果和中心点变化的函数plotdata。

# 定义可视化函数
def plotdata(data, centroids, clusted=None):   # data:数据， centroids:迭代后所有中心点， clusted:最后一次聚类结果
    colors = ['b','g','gold','darkorange','salmon','olivedrab',
              'maroon', 'navy', 'sienna', 'tomato', 'lightgray', 'gainsboro'
             'coral', 'aliceblue', 'dimgray', 'mintcream', 'mintcream']  # 定义颜色，用不同颜色表示聚类结果
 
    assert len(centroids[0]) <= len(colors), 'colors are not enough '  # 检查颜色和中心点维度
 
    clust_data = []  # 存储聚好类的数据,同一个类放在同一个列表中
    if clusted is not None:
        for i in range(centroids[0].shape[0]):
            x_i = data[clusted==i]
            clust_data.append(x_i)  # x_i is np.array
    else:
        clust_data = [data]  # 未进行聚类，默认将其作为一个类
 
    # 用不同颜色绘制数据点
    plt.figure(figsize=(8,5))
    for i in range(len(clust_data)):
        plt.scatter(clust_data[i][:, 0], clust_data[i][:, 1], color=colors[i], label='cluster %d'%(i+1))
 
    plt.legend()
    plt.xlabel('x', size=14)
    plt.ylabel('y', size=14)
 
    # 绘制中心点
    centroid_x = []
    centroid_y = []
    for centroid in centroids:
        centroid_x.append(centroid[:,0])
        centroid_y.append(centroid[:,1])
    plt.plot(centroid_x, centroid_y, 'r*--', markersize=14)
    plt.show()

将数据集和初始质心带入plotdata函数进行测试，画出的是原始样本点。

plotdata(X, [centroids])

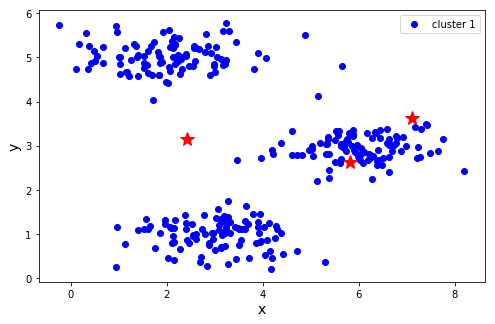
第五步 进行训练,迭代30次。

# 进行训练
def run_k_means(Datas, centroids, iters):
    all_centroids = [centroids]
    for i in range(iters):
        clusted = findClosestCentroids(Datas, centroids)
        centroids = computMeans(Datas, clusted)
        all_centroids.append(centroids)
    return clusted, all_centroids
 
clusted, all_centroids = run_k_means(X, np.array([[3,3], [6,2], [8,5]]), 30)
 
plotdata(X, all_centroids, clusted)

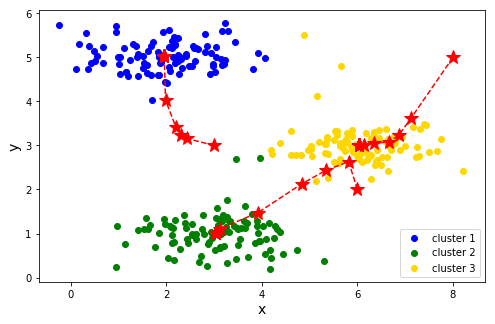
以上过程选取的质心是自己给定的，实际应用中一般是随机给定的。随机给定方法中可以先找出样本在每一维度的最小值和最大值，然后每一维度选取最小值到最大值之间的数，不同维度合并成初始质心点。也可以从样本点中随机选取k个质心。

# 方案一 先找出数据集每一列的最大值和最小值，然后在最大和最小之间随机生成
def randCent(Datas, k):
    n = np.shape(Datas)[1]  # 数据集维度
    centroids = np.mat(np.zeros((k, n)))  # 给质心赋0值
    for i in range(n):
        min_i = min(Datas[:, i])
        range_i = float(max(Datas[:, i]) - min_i)
        centroids[:, i] = min_i + range_i*np.random.rand(k, 1)
    return np.array(centroids)
 
randCent(X, 3)

# 方案二 从数据集去随机选取K个样本作为初始质心
def randCent(Datas, k):
    n = Datas.shape[0]
    random_index = np.random.choice(n, k)
    centroids = Datas[random_index]
    return centroids
randCent(X, 3)

第二题  压缩图片

在这个题目中看，用一个简单的24位颜色表示图像。每个像素被表示为三个8位无符号整数(从0到255)，指定了红、绿和蓝色的强度值。这种编码通常被称为RGB编码。我们的图像包含数千种颜色，在这一部分的练习中，你将把颜色的数量减少到16种颜色，这可以有效地压缩照片。具体地说，您只需要存储16个选中颜色的RGB值，而对于图中的每个像素，现在只需要将该颜色的索引存储在该位置(只需要4 bits就能表示16种可能性)。 如果图像是128×128的，那么图像经过压缩后由原来的128×128×24 = 393,216 位变为了 16 × 24 + 128 × 128 × 4 = 65,920 位。

接下来我们要用K-means算法选16种颜色，用于图片压缩。你将把原始图片的每个像素看作一个数据样本，然后利用K-means算法去找分组最好的16种颜色。

第一步 引入图片（bird_small.png）

from skimage import io
 
sample_image = io.imread('./ex7/bird_small.png')
sample_image.shape

plt.imshow(sample_image)
plt.show()

第二步 随机初始化质心

sample_image = sample_image/255   # 将数据归一化到0-1
 
data = sample_image.reshape(-1, 3)  # 将图片像素大小重置，每一个像素点代表一个样本
print(data[:3])
print(data.shape)
k = 16  #  聚类个数
centroids = randCent(data, k)  # 随机初始化质心
centroids

第三步 训练

# 对其进行聚类， 迭代次数为30次
clusted, all_centroids = run_k_means(data, centroids, 30)

第四步 重构图片

img = np.zeros(data.shape)  # 初始化图片
last_centroids = all_centroids[-1]  # 最后一聚类质心
for i in range(len(last_centroids)):  # 利用聚类质心替换图片中元素
    img[clusted==i] = last_centroids[i]
 
img = img.reshape(128, 128, 3)  # 转换大小

第五步 对比前后效果

# 绘制图片
fig, axs = plt.subplots(1, 2, figsize=(10,6))
axs[0].imshow(sample_image)
axs[1].imshow(img)
plt.show()

四、k-means总结

优点：容易实现

缺点：可能收敛到局部最小值，在大规模数据集上的收敛速度较慢。

适用数据类型：数值型数据