UVa 1451 Average - 斜率优化

　　A DNA sequence consists of four letters, A, C, G, and T. The GC-ratio of a DNA sequence is the number of Cs and Gs of the sequence divided by the length of the sequence. GC-ratio is important in gene finding because DNA sequences with relatively high GC-ratios might be good candidates for the starting parts of genes. Given a very long DNA sequence, researchers are usually interested in locating a subsequence whose GC-ratio is maximum over all subsequences of the sequence. Since short subsequences with high GC-ratios are sometimes meaningless in gene finding, a length lower bound is given to ensure that a long subsequence with high GC-ratio could be found. If, in a DNA sequence, a 0 is assigned to every A and T and a 1 to every C and G, the DNA sequence is transformed into a binary sequence of the same length. GC-ratios in the DNA sequence are now equivalent to averages in the binary sequence.

Position Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Sequence	0	0	1	0	1	0	1	1	0	1	1	0	1	1	0	1	0

　　For the binary sequence above, if the length lower bound is 7, the maximum average is 6/8 which happens in the subsequence [7,14]. Its length is 8, which is greater than the length lower bound 7. If the length lower bound is 5, then the subsequence [7,11] gives the maximum average 4/5. The length is 5 which is equal to the length lower bound. For the subsequence [7,11], 7 is its starting index and 11 is its ending index.

　　Given a binary sequence and a length lower bound L, write a program to find a subsequence of the binary sequence whose length is at least L and whose average is maximum over all subsequences of the binary sequence. If two or more subsequences have the maximum average, then find the shortest one; and if two or more shortest subsequences with the maximum average exist, then find the one with the smallest starting index.

Input

　　Your program is to read from standard input. The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case starts with a line containing two integers n (1 ≤ n ≤ 100, 000) and L (1 ≤ L ≤ 1, 000) which are the length of a binary sequence and a length lower bound, respectively. In the next line, a string, binary sequence, of length n is given.

Output
　　Your program is to write to standard output. Print the starting and ending index of the subsequence.

Sample Input

Sample Output

---

　　按照题目意思，可以想出用前缀和，这样从i到j的平均数就可以表示为(sum[j] - sum[i - 1]) / j - i + 1，仔细一看，这长得不是很向斜率的公式吗？

　　那么我们可以把第i个字符抽象成平面上的点(i, sum[i])，题目就可以转换成已知平面上有N个点，找到两个点的横坐标的之差大于等于L,且斜率最大。然而这并没有什么用，因为刚刚要用O（n²）解决的问题，现在还是要用O（n²）来解决。不着急，来看看下面。

　　

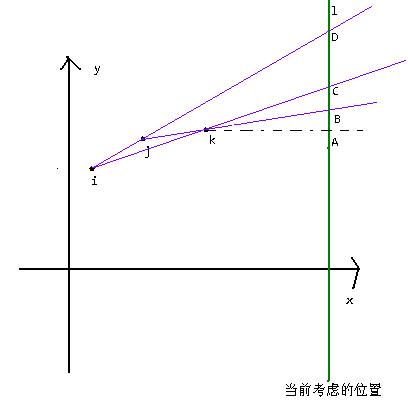
　　现在要确定以点p为结束位置的最优的起点，那么假如有i, j, k三个候选点，点p在直线l上。

• 如果点p在线段AB上，那么点i是最优的
• 如果点p在线段BC上，那么点i还是最优的
• 如果点p在线段CD上，那么点k还是最优的
• 如果点p在点D上方，那么点k还是最优的

　　于是，可以试问点j的意义。既然没有意义，那就把它删掉吧，于是最后的折线成了这样↓

　　

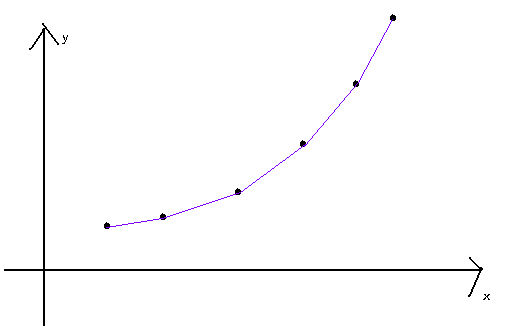
　　由于sum是递增的，所以对于两个存在于折线上的两个点i, j（i < j），如果i更优，那么还是i更优，如果j更优，那么i不会再更优（于是可以愉快地把i，pop()掉了）

　　所以处理以r为右端点的时候，先用点r - L删掉上凸点（维护斜率的递增），再把点r - L塞进去(push_back())，最后删掉队首没有第二个元素更优的队首，然后取出当前队首，更新答案。

　　由于这个队列允许队首删除，队尾插入和删除，所要实现双端队列（不要学习我封装）（似乎是单调队列）。
　　由于每个元素至多会被插入队列1次，从队列中删除1次，所以时间复杂度为O(n)，总时间复杂度为O(n)（常数又被省略掉了）

Code_{(无限wa后的ac代码)}

 /**
  * uva
  * Problem#1451
  * Accepted
  * Time:60ms
  */
 #include<iostream>
 #include<sstream>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cstring>
 #include<cctype>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #include<algorithm>
 using namespace std;
 typedef bool boolean;
 #define smin(a, b) (a) = min((a), (b))
 #define smax(a, b) (a) = max((a), (b))
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         aFlag = -;
         x = getchar();
     }
     for(u = x - ''; isdigit((x = getchar())); u = u *  + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 template<typename T>
 class IndexedDeque{
     public:
         T* list;
         int pfront;
         int prear;
         IndexedDeque():list(NULL), pfront(), prear(){        }
         IndexedDeque(int size):pfront(), prear(){
             list = new T[size];
         }
         void push_front(T x){    list[--pfront] = x;        }
         void push_back(T x)    {    list[prear++] = x;        }
         void pop_front()    {    ++pfront;                }
         void pop_back()        {    --prear;                }
         T     front()        {    return list[pfront];    }
         T     rear()            {    return list[prear - ];        }
         T& operator [](int pos){            return list[pfront + pos];        }
         int size()            {    return prear - pfront;    }
 };

 int T;
 int n, L;
 int* sum;
 char* str;
 IndexedDeque<int> que;

 inline int segsum(int from, int end){    return sum[end] - sum[from - ];    }
 inline int cmpSlope(int l1, int r1, int l2, int r2){    return (segsum(l1, r1) * (r2 - l2 + )) - (segsum(l2, r2) * (r1 - l1 + )); }

 inline void init(){
     readInteger(n);
     readInteger(L);
     str = new char[(const int)(n + )];
     sum = new int[(const int)(n + )];
     que = IndexedDeque<int>(n * );
     scanf("%s", str);
 }

 inline void solve(){
     sum[] = ;
     for(int i = ; i < n; i++)
         sum[i + ] = sum[i] + str[i] - '';

     int resl = , resr = L;
     for(int i = L; i <= n; i++){
         while(que.size() >  && cmpSlope(que[que.size() - ], i - L, que[que.size() - ], i - L) >= )
             que.pop_back();
         que.push_back(i - L + );
         while(que.size() >  && cmpSlope(que[], i, que[], i) <= )
             que.pop_front();

         int temp = cmpSlope(que.front(), i, resl, resr);
         if(temp >  || (temp ==  && resr - resl > i - que.front())){
             resl = que.front(), resr = i;
         }
     }
     printf("%d %d\n", resl, resr);
 }

 inline void clear(){
     delete[] sum;
     delete[] str;
     delete[] que.list;
 }

 int main(){
     readInteger(T);
     while(T--){
         init();
         solve();
         clear();
     }
     return ;
 }