机器学习入门-线性判别分析（LDA）1.LabelEncoder(进行标签的数字映射) 2.LinearDiscriminantAnalysis (sklearn的LDA模块)

1.from sklearn.processing import LabelEncoder 进行标签的代码编译

首先需要通过model.fit 进行预编译，然后使用transform进行实际编译

2.from sklearn.discriminant_analysis import LinearDiscriminantAnalysis  as LDA  从sklearn的线性分析库中导入线性判别分析即LDA

用途：分类预处理中的降维，做分类任务

目的：LDA关心的是能够最大化类间区分度的坐标轴

将特征空间（数据中的多维样本，将投影到一个维度更小的K维空间，保持区别类型的信息）

监督性：LDA是“有监督”的，它计算的是另一个类特定的方向

投影：找到更适用的分类空间

与PCA不同： 更关心分类而不是方差（PCA更关心的是方差）

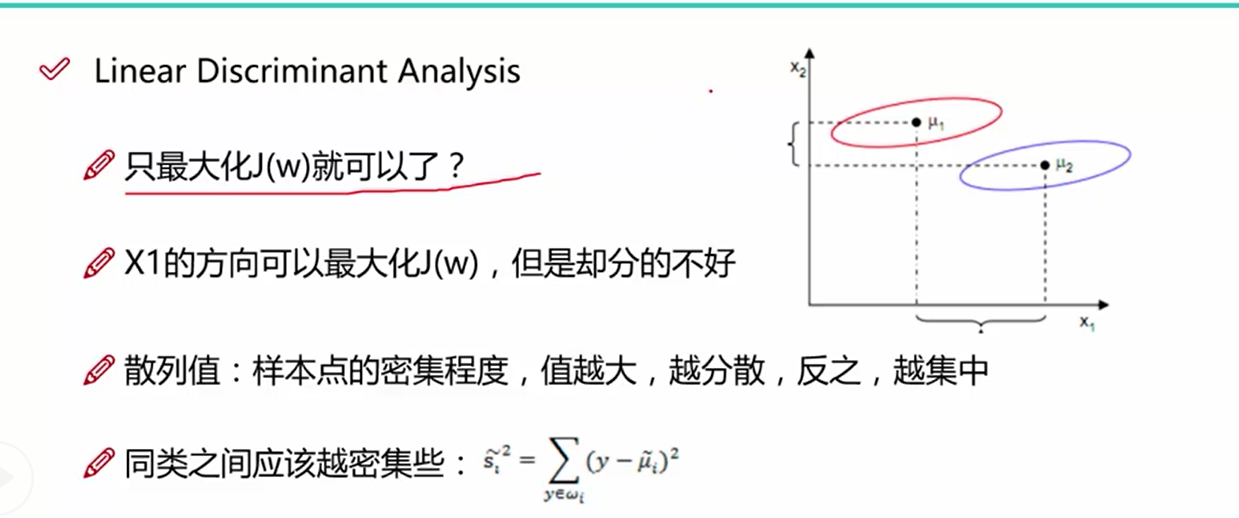
如图所示，找到合适的方向投影后的数据更加的分散

LDA的数据原理：

目标找到投影：y = w^T * x  ,我们需要求解出w

LDA的第一个目标是使得投影后两个类别之间的距离越大越好，使用的判别依据，是投影后两个类别的中心点的距离越大越好，即均值u1^ - u2^

第一步：求出当前均值和投影后的均值

J(W) = |w^T(u1 - u2)|   # 计算投影以后的两个类别中心位置之差

LDA的第二个目标是使得投影后的类别之间的距离越来越小，从图一中我们可以看出，只讨论类别之间的距离是不够的， 同类之间的距离使用单个类别的数据到类别中心之差来表示，值越大，同类数据越分散，值越小，同类数据越集中，我们需要使得这个值的大小越小越好

根据上面两个目标函数，我们做一个组合， 分子使用类间距离， 分母使用类内距离，求得组合后的最大值

该图表示的是最终的目标函数（类间距离/类内距离），这里的类内散布矩阵：通过同种类别数据-该类别的均值之差进行加和后求得

求得类间距离的散步矩阵

上述的目标矩阵就是我们求解的方程，我们需要求得其最大值

构造拉格朗日方程， 我们对分母进行缩放，使得w^TSw*w = 1, 作为限制条件

cw = w^T*SB*w - a(w^T*Sw*w-1) --构造的拉格朗日方程

cw/dw = w^T*SB*w - a(w^T*Sw*w-1) / dw   对上述方程使用dw进行求导，求偏导等于零求最大值

2SB*w - 2*a*Sw * w = 0

a * w = Sw^-1*SB*w  ---- a*w = A*w

w是Sw^-1*SB的特征向量

代码：自己自行的编写

第一步：读取数据

第二步：提取样本变量和标签

第三步：对标签进行数字映射，使用LableEncoder

第四步：计算类内散列矩阵Sw sum((x-ui).dot((x-ui).T))

第五步：计算类间散列矩阵SB sum(n*(ui-u).dot(ui-u))  ui表示每一类样本的均值, u表示所有样本的均值

第六步：计算Sw^-1*SB的特征向量，即w，如果我们投影的维度是2，使用np.vstack, 将求得的特征向量的第一列和第二列数据进行拼接

第七步：将二维的w和X特征进行点乘操作， 获得变化后的二维特征

第八步：进行画图操作

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 第一步数据载入
data = pd.io.parsers.read_csv(filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
                              header=None, names=['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm', 'names'],
                             sep=',',)
data.dropna(how='all', inplace=True)

# 第二步提取数据的X轴和y轴信息
feature_names = ['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm']
X = data[feature_names].values
y = data['names'].values

# 第三步 使用Label_encoding进行标签的数字转换
from sklearn.preprocessing import LabelEncoder

model = LabelEncoder().fit(y)
y = model.transform(y) + 1

labels_type = np.unique(y)

# 第四步 计算类内距离Sw
Sw = np.zeros([4, 4])
# 循环每一种类型
print(labels_type)
for i in range(1, 4):
    xi = X[y==i]
    ui = np.mean(xi, axis=0)
    sw = ((xi - ui).T).dot(xi-ui)
    Sw += sw
print(Sw)

# 第五步：计算类间距离SB
SB = np.zeros([4, 4])
u = np.mean(X, axis=0).reshape(4, 1)
for i in range(1, 4):
    n = X[y==i].shape[0]
    u1 = np.mean(X[y==i], axis=0).reshape(4, 1)
    sb = n * (u1 - u).dot((u1 - u).T)
    SB += sb

# 第六步：使用Sw^-1*SB特征向量计算w
vals, eigs = np.linalg.eig(np.linalg.inv(Sw).dot(SB))

# 第七步:取前两个特征向量作为w，与X进行相乘操作，相当于进行了2维度的降维操作
w = np.vstack([eigs[:, 0], eigs[:, 1]]).T

transform_X = X.dot(w)

# 第八步:定义画图函数
labels_dict = data['names'].unique()
def plot_lda():

    ax = plt.subplot(111)
    for label, m, c in zip(labels_type, ['*', '+', 'v'], ['red', 'black', 'green']):
        plt.scatter(transform_X[y==label][:, 0], transform_X[y==label][:, 1], c=c, marker=m, alpha=0.6, s=100, label=labels_dict[label-1])

    plt.xlabel('LD1')
    plt.ylabel('LD2')
    # 定义图例，loc表示的是图例的位置
    leg = plt.legend(loc='upper right', fancybox=True)
    # 设置图例的透明度为0.6
    leg.get_frame().set_alpha(0.6)
    #坐标轴上的一簇簇的竖点
    plt.tick_params(axis='all', which='all', bottom='off', left='off', right='off', top='off',
                    labelbottom='on', labelleft='on')
    # 表示的是坐标方向上的框线
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)
    ax.spines['right'].set_visible(False)

    plt.tight_layout()
    plt.grid()
    plt.show()

plot_lda()

我们使用Sklearn自带的程序进行操作

第一步：读取数据

第二步：提取特征

第三步：对标签做数字映射，使用的是LabelEncoder

第四步：使用from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

第五步：结果进行画图

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 第一步数据载入
data = pd.io.parsers.read_csv(filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
                              header=None, names=['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm', 'names'],
                             sep=',',)
data.dropna(how='all', inplace=True)

# 第二步提取数据的X轴和y轴信息
feature_names = ['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm']
X = data[feature_names].values
y = data['names'].values

# 第三步 使用Label_encoding进行标签的数字转换
from sklearn.preprocessing import LabelEncoder

model = LabelEncoder().fit(y)
y = model.transform(y) + 1

labels_type = np.unique(y)

# 第四步 建立LDA模型
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

model = LDA(n_components=2)
sklearn_x = model.fit_transform(X, y)

# 第五步进行画图操作
def plot_lda_sklearn(X, title):

    ax = plt.subplot(111)
    for label, m, c in zip(labels_type, ['*', '+', 'v'], ['red', 'black', 'green']):
        plt.scatter(X[y==label][:, 0], X[y==label][:, 1], c=c, marker=m, alpha=0.6, s=100, label=labels_dict[label-1])

    plt.title(title)
    plt.xlabel('LD1')
    plt.ylabel('LD2')
    leg = plt.legend(loc='upper right', fancybox=True)
    leg.get_frame().set_alpha(0.6)

    plt.tick_params(axis='all', which='all', bottom='off', left='off', right='off', top='off',
                    labelbottom='on', labelleft='on')
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)
    ax.spines['right'].set_visible(False)

    plt.tight_layout()
    plt.grid()
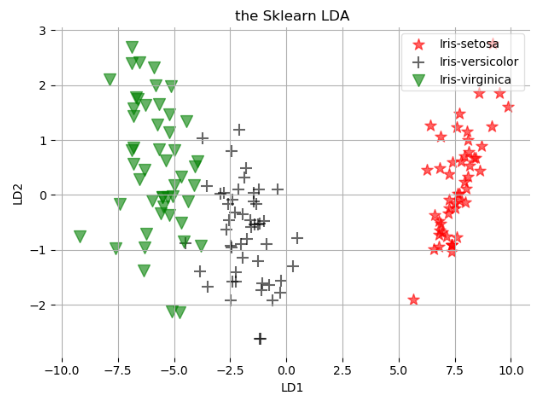
    plt.show()

plot_lda_sklearn(sklearn_x, 'the Sklearn LDA')