perl6中的q/qq/qx/qqx
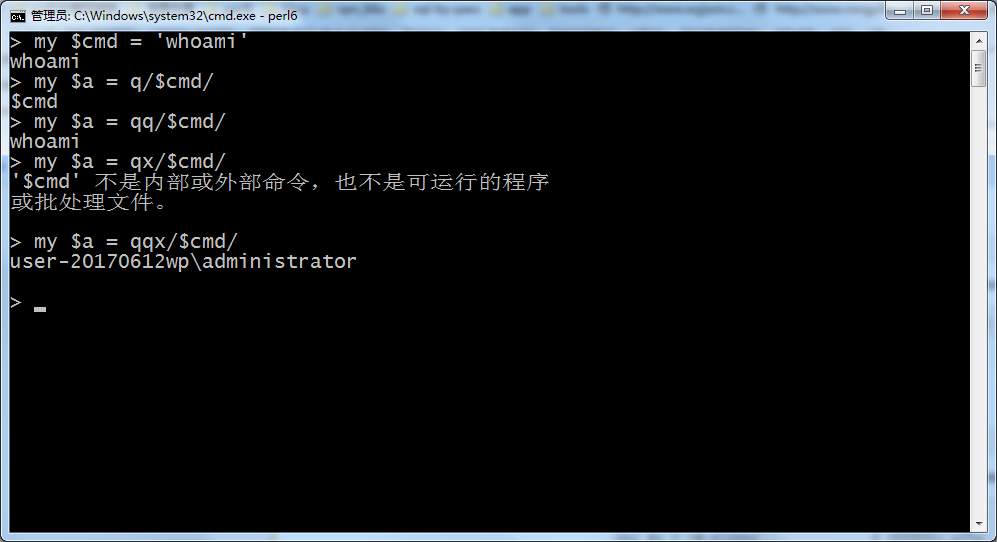
q不内插
qq内插
qx不内插
qqx内插
perl6中的q/qq/qx/qqx的更多相关文章
- 网页中如何启用QQ交谈
很多网友都会发现好多的网页中会有诸如,网页中如何启用QQ交谈? 1. 登录QQ, 打开网址:http://shang.qq.com/v3/widget.html 启用QQ通讯组件. 2. 选择组件样式 ...
- 形象的讲解angular中的$q与promise(转)
以下内容摘自http://www.ngnice.com/posts/126ee9cf6ddb68 promise不是angular首创的,作为一种编程模式,它出现在……1976年,比js还要古老得多. ...
- Solr中的q与fq参数的区别
转自:搜索系统5:Solr中的q与fq参数的区别在那儿 1.对结果排序有影响 今天遇到一个问题,把相同的参数比如name:张三,放到q与fq,两者返回的结果完全不一样. 经过debug发现,原因是这两 ...
- Angular中的$q的形象解释及深入用法
作者:寸志链接:https://zhuanlan.zhihu.com/p/19622332来源:知乎著作权归作者所有.商业转载请联系作者获得授权,非商业转载请注明出处. 早上,老爸说:“儿子,天气如何 ...
- 原创:形象的讲解angular中的$q与promise
promise不是angular首创的,作为一种编程模式,它出现在……1976年,比js还要古老得多.promise全称是 Futures and promises.具体的可以参见 http://en ...
- perl6中的替换
use v6; =begin pod perl6 中的替换用S/// S有几个可选参数: :g —(长形式::global)全局匹配:替换掉所有的出现 :i —不区分大小写的匹配 :ii —(长形式: ...
- perl6中的hash定义(2)
use v6; , :b, :!c; say %ha; say %ha<a>; #这里不能用%ha{a}, {a}表示调用a()函数了, 在perl6中, {}有特别函义 say %ha{ ...
- 在 Visual Studio 中使用 Q# 进行量子编程
1 量子计算机与量子编程 1.1 量子计算机 Quantum computing is computing using quantum-mechanical phenomena, such as su ...
- perl q qq qr qw qx 区别与使用方法
1.q 相当于 单引号' ' 转义字符无效 q可以使用()[] {} // ,, 2.qq 相当于" " 转义字符有效 qq可以使用()[] {} // ,, 3.qw 相当于 ...
随机推荐
- 将下载到本地的JAR包手动添加到Maven仓库(转)
常用Maven仓库网址:http://mvnrepository.com/http://search.maven.org/http://repository.sonatype.org/content/ ...
- BZOJ 1787 紧急集合(LCA)
转换成抽象模型,就是要求一棵树(N个点,有N-1条边表示这个图是棵树)中某一点满足给定三点a,b,c到某一点的距离和最小.那么我们想到最近公共祖先的定义,推出只有集合点在LCA(a,b).LCA(a, ...
- 【bzoj1877】[SDOI2009]晨跑 费用流
题目描述 Elaxia最近迷恋上了空手道,他为自己设定了一套健身计划,比如俯卧撑.仰卧起坐等 等,不过到目前为止,他坚持下来的只有晨跑. 现在给出一张学校附近的地图,这张地图中包含N个十字路口和M条街 ...
- BZOJ4767 两双手(组合数学+容斥原理)
因为保证了两向量不共线,平面内任何一个向量都被这两个向量唯一表示.问题变为一张有障碍点的网格图由左上走到右下的方案数. 到达终点所需步数显然是平方级别的,没法直接递推.注意到障碍点数量很少,那么考虑容 ...
- Python文件传输模块ftplib
ftplib是基于FTP协议实现的一个Python模块 from ftplib import FTP # 创建一个FTP连接对象 ftp = FTP() #[ 当带有参数时,即:ftp = FTP(h ...
- Codeforces Gym 101142 C. CodeCoder vs TopForces(思维+图论)
题意: 每个人有两个积分CC和TF 第i个人能战胜第j个人的条件满足下面两个条件中的一个即可 1.CCi > CCj 或 TFi > TFj 2.i能战胜k,k能战胜j. 题解: 先按CC ...
- [JSOI2007]重要的城市 floyd:最短路计数
---题面--- 题解: 其实感觉还是比较妙的,第一眼看题想到floyd统计最短路条数, 注意到对于任意两点x,y而言,floyd将会枚举其最短路所可能经过的所有中转点, 因此我们可以直接分别统计对于 ...
- Android APP性能优化(最新总结)
导语 安卓大军浩浩荡荡,发展已近十个年头,技术优化日异月新,如今Android 8.0 Oreo 都发布了,Android系统性能已经非常流畅了.但是,到了各大厂商手里,改源码自定系统,使得And ...
- [CEOI2017]Mousetrap
P4654 [CEOI2017]Mousetrap 博弈论既视感 身临其境感受耗子和管理的心理历程. 以陷阱为根考虑.就要把耗子赶到根部. 首先一定有解. 作为耗子,为了拖延时间,必然会找到一个子树往 ...
- angularJS批量删除 品优购删除品牌(通用复选框批量选中删除解决思路)
思路: 一步:在点击复选框时维护变量数组 在js中定义一个数组变量, 给复选框添加点击动作, 在动作中判断当前复选框是否为选中状态(即点击后复选框的是否选中状态), 若为选中状态,则向数组中添加选中的 ...
