C指针（4）——数据结构中指针的应用（非常重要）

5-1动态内存分配，分配的是堆内存的空间

• 分配内存函数 (都集中在库函数 stdlib.h  中)

void *malloc (unsigned int num_bytes); //指定分配内存空间大小，大小为 num_bytes字节，其值是随机值。
void *calloc (unsigned num ,unsigned size);  //参数包含元素的数量和每个元素的字节数，内存空间为num*sie
void *realloc(void *ptr,size_t size);  //调用该函数对内存空间进行重新分配，ptr指向已有的内存空间，size用来指定重新分配后所得整个空间大小

　   在使用动态分配之前，首先要判断是否分配成功。

• 内存的释放函数原型:

void free(void *ptr);   //动态分配的内存使用结束后，要及时释放，

　　内存释放后建议把指针指向NULL

5-2队列（初始化，入队，出队，判断空，判断满）

• 单向队列

　　

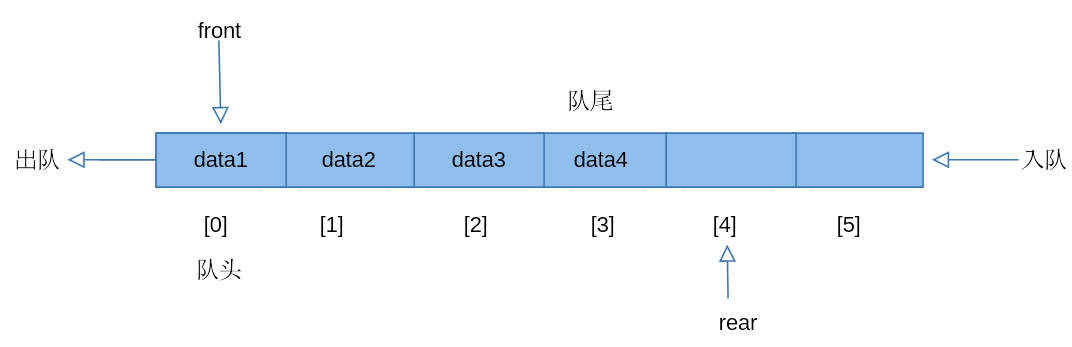
• 循环队列  （队头和队尾有两种情况会指向同一位置，一是队列空了，二是队列满了）

#define QueueSize_UartLen 8
typedef struct
{
  int front;   //队头
  int rear;    //队尾
  int counter;   //记录队列元素的个数
  int uart_data[QueneSize_UartLen];  //定义数组用来存储队列的元素
}CIRQUEUE_UART;    //定义结构体，用typedef把结构体重新命名为CIRQUEUE_UART

void InitQueue(CIRQUEUE_UART *queue) //初始化形参，CIRQUEUE_UART类型的指针变量queue，队列的初始化
{
  queue->front=0;   //->与指向结构体变量的指针相连，表示指向结构体变量指针的成员（左边为指针，注意与 . 的区别）
  queue->rear=0;
  queue->counter=0;
}

int Inqueue(CIRQUEUE_UART *queue,int data)  //入队
{
  if(QueueFull(queue))   //队满判断
   {
      return 0;         //输出队满提示
   }
   else
   {
      queue->uart_data[queue->rear]=data;    //queue->rear指向队尾待插入数据位置
      queue->counter++;                      //计数器加1
      queue->rear=(queue->rear+1)%QueueSize_UartLen;  //然后指queue->rear向下一个待插入数据的位置
      return 1;
   }
}

int OutQueue(CIRQUEUE_UART *queue,int *p_data)    //出队  通过指针p_data取出队的数据
{
  if(QueueEmpty(queue))
    {
     return 0;
     }
   else
     {
      *p_data=queue->data(front);         //先把出队的数据元素取出放在p_data
      queue->counter--;                   //计数器减1
      queue->front=(queue->front+1)%QueueSize_UartLen;   //然后指queue->front向下一个位置
      return 1;
      }
}

int QueueEmpty(CIRQUEUE_UART *queue)  //判断队空
{
  return queue->count==0;
}

int QueueFull(CIRQUEUE_UART *queue)   //判断队满
{
  return queue->counter==QueueSize_UartLen;
}

• 链式队列

　　构成链表中的每一个存储节点都包括一个值域和一个指针域，而指针域指向的是下一个存储节点的，则称该链表为单链表，在一个单链表中第一个节点的指针称为表头指针，最后一个节点被称为表尾节点，表尾节点的指针域的值为空。

　　在一个单链表中，除表头节点外，每一个每个结点都由前一个结点的指针域所指向，第一个节点只能有另设的表头指针所指向。当访问一个单链表时候，只能从表头指针出发，首先访问第一个节点，然后由第一个节点的指针域指向第二个节点的地址。

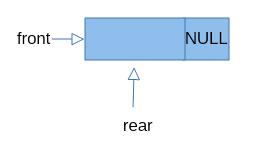　　空队列时，头指针front和尾指针rear都指向头结点。

　　

　　单链表只要头节点就可以访问所有的链表元素，融入队列的特性，一个指针是不不够的。队列删除（出队）在对头，插入（入队）在队尾。

　　头指针front指向链队的头结点，每个结点对应一个数据；尾指针rear指向终端结点。

typedef struct LinkNode_t       //队列结点结构
{
  int data;
  struct LinkNode_t *next;
}LinkNode;
typedef struct LinkPoint_t      //队列链表结构
{
  struct LinkNode_t *front;
  struct LinkNode_t *rear;
}LinkQueue;
LinkQueue *queue;
LinkNode *node;

LinkQueue LinkQueueInit()                       //初始化，建立一个带有队头的空队列
{
  queue_t=(LinkQueue)malloc(sizeof(LinkQueue)); //因为在LinkQueue中定义了一个结构体指针，必须对其进行分配内存。
  node=(LinkQueue)malloc(sizeof(LinkNode));     //同上
  node->next=NULL;
  queue_t->front=queue->rear=node;
  return queue_t;
}

void InlinkQueue(LinkQueue *queue,int data)  //入队
{
  node=(LinkNode)malloc(sizeof(LinkNode));
  node->data=data;
  node->next=queue->rear->next; //node->next指向data插入前、尾部指针指向的next的位置（queue->rear->next）。
  queue->rear->next=node;     //新插入的数据或结点成了新的队尾，队尾指针queue->rear->next指向新插入的node结点
  queue->rear=node;           //最后让新插入的数据或结点成为新的队尾。
}

void OutQueue(LinkQueue *queue)  //出队
{
  int data;
  if(!LQEmpty(queue))         //判空
  {
    node=queue->front->next;
    queue->front->next=node->next;
    data=node->data;
    if(node==queue->rear)        //如果只有一个元素，当他出队时队列就成了空队，需要修改为尾部指针
      {
         queue->rear=queue->front;
      }
     free(node);
     return data;
  }
}

int LQEmpty(LinkQueue *queue)   //对空判断
{
   if(queue->front==queue->rear)
    {
      return 1;
    }
    else
    {
      return 0;
    }
}

　　链队没有判断队满的情况，实际操作没有必要，因为链队继承了动态链表的操作。入队时会进行动态分配内存空间，出队时，则进行了释放。

　　补充：结构体中定义另外一个结构体。

5-3堆栈（初始化，进栈，出栈，栈空的判断，栈满的判断，取栈顶元素）

　　

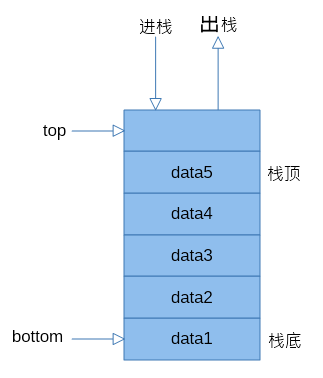
1.采用指向栈顶、栈底两个指针时：
typedef struct
{
  int top;
  int data[10];
  int bottom;
}stack_rf;
stack_rf *p_rf_data;  //

p_rf_data->top-p_rf_data->bottom==10; //判断栈是否为满
p_rf_data->top-p_rf_data->bottom==0;  //判断栈是否为空

*(p_rf_data->top-1)  //栈顶元素
*(p_rf_data->bottom) //栈底元素

2.只采用栈顶一个指针时：
#define Len_Uart 10;
typedef struct
{
  int top;
  int uart_data[Len_Uart];
}stack_uart;

void InitStack(stack_uart *stack)
{
  stack->top=0;      //栈的初始化
}

int PushStack(stack_uart *stack,int data) //进栈
{
  if(StackFull(stack))   //栈满判断
  {
    //输出栈满提示
    return(0);
  }
  else
  {
    stack->uart_data[stack->top]=data;
    stack->top++;
    return(1);
  }
}

int PopStack(stack_uart *stack)  //出栈
{
  int data;
  if(StackEmpty(stack))  //栈空判断
  {
    return 0;  //输出栈空提示
  }
  else
  {
    stack->top--;
    data=stack->data[stack->top];
    return data;
  }
}

int StackEmpty(stack_uart *stack)  //栈空判断
{
  return(stack->top==0);
}

int StackFull(stack_uart *stack)   //栈满判断
{
  return(stack->top==Len_Uart);
}

int StackTop(stack_uart *stack,int *p_topdata)  //取栈顶元素
{
  if(StackEmpty())
  {
    //输出栈空提示
    return 0;
  }
  else
  {
   *p_topdata=stack->uart_data[stack->top-1];
   return 1;
   }
}

5-4链表（链表建立，链表初始化，链表插入，链表删除）

　　

　　单链表：头结点没有值域，只有链域。专门存放第一个结点的地址。尾结点，有值域也有链域，链域始终为NULL。

　　           

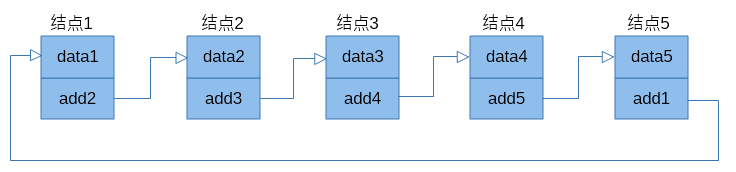
　　循环链表：由单链表演变而来，循环链表的尾结点的链域指向链表头的结点

　　两者区别：（1）单链表需要专门创建一个头结点存放第一个节点的地址，尾部节点链域为NULL；循环链表不需要，只是最后一个链域指向表头结点。

　　　　　　　（2）链尾判断，单链表只需要判断链域值是否为NULL；循环链表只需要判断该结点的链域值是否指向链表头结点。

typedef struct LinkNode    //定义链表结点类型
{
  int data;
  struct LinkNode *next;
}*List;

List InitList(void)   //链表初始化
{
  List linknode_t;
  linknode_t=(list)malloc(sozeof(list));  //动态分配内存空间给linknode_t
  if(!linknode_t)
   {
     //输出失败提示
    return 0;
   }
   else
   {
     linknode_t->next=linknode_t;
     return linknode_t;
   }
}

List g_DebiList;
int main(void)   //在main中调用InitList()函数
{
  g_DevList=InitList();
  return 0;
}

链表的操作
typedef struct DEVICE_PROPERTY_t
{
  int data;
  struct DEVICE_PROPERTY_t *next;
}DEVICE_PROPERTY_t;
typedef unsigned char uint8_t;
#define DEVICELIST_MAX 5;
DEVICE_PROPERTY_t g_RegDeviceList[DEVICELIST_MAX];
DEVICE_PROPERTY_t *g_LastRegDevice;
uint8_t g_DeviceCnt=0;

voide DevListInit(void)      //链表初始化
{
  uint8_t i;
  for(i=0;i<DEVICELIST_MAX;i++)
  {
   g_RegDeviceList[i].next=NULL;
  }
   g_lastRegDevice=NULL;
   g_DeviceCnt=0
}

DEVICE_PROPERTY_t *FindVacancy(void)  //寻找插入点
{
  uint8_t i;
  if(g_DeviceCnt<DEVICELIST_MAX)
  {
    for(i=0;i<EEVICELIST_MAX;i++)
    {
       if(g_RegDeviceList[i].next==NULL)
         {
           return(&g_RegDeviceList[i]);
         }
     }
    return 0;
  }
   else
   {
    return(NULL);
   }
}

uint8_t Insert(uint8_t data)     //链表插入
{
  DEVICE_PROPERTY_t *tempptr,*ptr;
  temptr =FindVacancy();
  if(tempptr!=null)
   {
     tempptr->data=data;
       if(!g_DeviceCnt)
        {
          tempptr->next=tmpptr;
          g_ListRegDevice=tempptr;
        }
        else
        {
           ptr=g_LastRegDevice->next;   //暂存原来尾结点的链域
           g_LastRegDevice->next=tempptr;  //让原来尾结点的链域指向新插入的结点，即g_LastRegDevice->next=tempptr;
           tempptr->next=ptr;              //让新插入的结点成为尾结点，即链域指向原来尾结点链域所指向的位置
         }
         g_DeviceCnt++;
         return 1;
   }
   return 0;
}

uint8_t DeleteDevicefromlist(uint8_t data)  //链表删除（data即为要删除的结点）
{
  uint8_t i,j;
  DEVICE_PROPERTY_t *nextdevice;
  for(i=0;i<g_DeviceCnt;i++)    //通过判断来指定结点的值域是否是要删除的值域data
  {
    if(g_LastRegDevice->data==data)
      {
        nextdevce=g_ListRegDevice->next; //将该结点的链域指向的结点指针，也就是将要删除的结点的下一个结点
        g_LastRegDevice->next=NULL;       //把该节点的链域置为NULL
        g_DeviceCnt--;
        g_LastRegDevice=nextdevice;    //让删除结点的下一个结点成为尾结点（删除是操作的逆过程）
        if(g_DeviceCnt)
         {
           for(j=0;j<g_DeviceCnt-1;j++)
             {
                g_ListRegDevice->next=nextdevice;
              }
              g_ListRegDevice->next=nextdevice;
          }
         return 1;
      }
     g_LastRegDevice=g_LastRegDevice->next;
   }
  return 0;
}

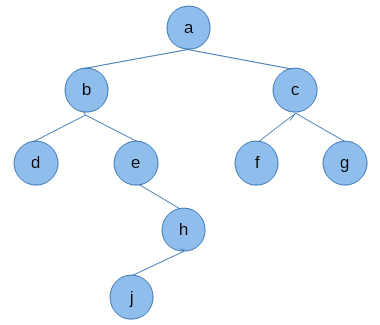
5-5树

　　树为非线性结构，对于二叉树首先是二叉树的创建和遍历

typedef struct tree_node   //运用链式存储结构
{
    char data;                    //一个值域两个链域，值域存储结点本身的数值
    struct tree_node *lchild,*rchild;           //链域分别存储结点左子树和又子树的地址
}BT_Node;
BT_Node *tree;  //定义一个指针tree，用来执行那个即将建立的树

BT_Node *Creat_BTree(BT_Node *tree)     //创建二叉树
{
   char ch;
   ch=getchar();        //从键盘输入一个字符，
   if(ch=='*')
   {
    tree=NULL;
   }
   else               //如果不是字符，则分配存储空间
    {
       tree=(BT_Node *)malloc(Tree_NodeLen);
       tree->data=ch;
       tree->lchild=Creat_BTree(tree->lchild);  //调用创建函数本身，创建结点的左子树和又子树（这是函数的递归调用）
       tree->rchild=Creat_BTree(tree->rchild);
    }
    return(tree);
}

　二叉树分为：前序遍历，中序遍历，后序遍历

示例：二叉树3种遍历方式的应用　

#include <stdio.h>
#include <malloc.h>

typedef struct tree_node
{
	char data;
	struct tree_node *lchild,*rchild;
}BT_Node;

#define Tree_NodeLen sizeof(BT_Node)
BT_Node *tree;
BT_Node *Creat_BTree(BT_Node *tree);
void Visit_Node(BT_Node *tree);
void Pre_Order(BT_Node *tree);
void Mid_Order(BT_Node *tree);
void After_Order(BT_Node *tree);
int main(void)
{
	printf("请输入树节点：\n");
	tree=Creat_BTree(tree);
	if(tree)
	{
	  printf("\n前序遍历:\n");
	  Pre_Order(tree);
	  printf("\n");

	  printf("\n中序遍历:\n");
	  Mid_Order(tree);
	  printf("\n");

	  printf("\n后序遍历:\n");
	  After_Order(tree);
	  printf("\n");
	}
	printf("\n");
  return 0;
}

BT_Node *Creat_BTree(BT_Node *tree)
{
  char ch;
  ch=getchar();
  if(ch=='*')
  {
    tree=NULL;
  }
  else
  {
    tree=(BT_Node *)malloc(Tree_NodeLen);
	tree->data=ch;
	tree->lchild=Creat_BTree(tree->lchild);
	tree->rchild =Creat_BTree(tree->rchild );
  }
  return(tree);
}

void Visit_Node(BT_Node *tree)
{
    printf(" ");
	putchar(tree->data);
	printf("\t");
}

void Pre_Order(BT_Node *tree)
{
	if(!tree)
	{
	   return ;
	}
	else
	{
	   Visit_Node(tree);
	   Pre_Order(tree->lchild );
	   Pre_Order(tree->rchild );
	}
}

void Mid_Order(BT_Node *tree)
{
	if(!tree)
	{
		return;
	}
	else
	{
		Mid_Order(tree->lchild );
		Visit_Node(tree);
		Mid_Order(tree->rchild );
	}
}

void After_Order(BT_Node *tree)
{
	if(!tree)
	{
		return;
	}
	else
	{
	    After_Order(tree->lchild );
		After_Order(tree->rchild );
		Visit_Node(tree);
	}
}