ACM 博弈（难）题练习 (第二弹)

第一弹：

---

Moscow Pre-Finals Workshop 2016 - Kent Nikaido Contest 1 Problem K. Pyramid Game

http://opentrains.snarknews.info/~ejudge/team.cgi?SID=afa73761fd0d61ae&action=2&lt=1

题意：

N堆石头，两个人轮流取。有2种操作：一是选择一堆石头拿走一个，二是从每堆石头拿走一个，但是只有当所有堆都非零的时候才能用第二种操作。 谁不能操作谁就输了。

题解：
1. 如果只有第一种操作，那么如果轮到某个人的时候剩下奇数个石头，他就可以赢。定义这样的局面是对他有利的。

2. 如果N为奇数，用第二种操作实际上不会改变局面对谁有利。 直接根据sum的奇偶判断。

3. 如果N为偶数，那么用一次第二种操作可以改变局面对谁有利。 考虑如果轮到某个人时，存在某一堆石头只有1个，那么如果当前局面对他有利，他直接用操作一拿走这个石头，如果对他不利，先手可以用一次操作二， 之后两个人都不能用操作二了。 所以不管怎样都是他赢。  换一个角度来看，如果某堆石头只有2个，那么显然不能去动它，否则就会把一个1留给对手。  因此问题转化为将每一堆石头都减去2个的子问题。   所以不断转化为子问题，只要考虑最少的那堆石头的奇偶性和sum的奇偶性就可以判断出答案了。

 #include <bits/stdc++.h>
 using namespace std;

 int main()
 {
     int n, a[];
     cin >> n;
     int s = , mi = ;
     for (int i = ; i <= n; ++i)
     {
         cin >> a[i], s += a[i], mi = min(mi, a[i]);
     }

     if (n & )
     {
         if (s & ) puts("Iori");
         else puts("Yayoi");
     }
     else
     {
         if (mi & ) puts("Iori");
         else
         {
             if (s & ) puts("Iori");
             else puts("Yayoi");
         }
     }

     return ;
 }

---

XVIII Open Cup named after E.V. Pankratiev. Ukrainian Grand Prix  Problem G Zenyk, Marichka and Interesting Game

http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=10396&locale_id=0

题意：
两个人玩取石子游戏，N堆石子，每次先手只能从某一堆石子里拿A个，后手只能从某一堆石子里拿B个，谁不能操作谁就输了。

题解：

1.如果A = B。显然对于一堆有$x$个石头的石子，只能操作$\lfloor \frac{x}{A} \rfloor $次，求和根据奇偶判断就好了。

2.如果A > B。

首先考虑所有堆的石子数都小于$A + B$的情况，这样对于每一堆石头，一个人取过，另一个人就不能再取了，而且先手在任意一堆上只能操作1次，后手则可能操作多次。先去掉那些$<B$的堆，即两个人都不能取的堆。

如果剩下偶数堆，那么先手必败，因为先后手都能取走一半的堆。

如果剩下奇数堆，如果存在一些堆的石头数 $ < A $&& $ >= B $, 即只有后手能取，那么后手必胜，因为后手可以比先手多取一些堆。 接着考虑如果某一堆石头$>= 2 * B$，后手肯定会抢这堆石头，因为这堆时候允许它操作多次。如果不存在这样特殊的堆，那么先手可以比后手多取走一堆，先手胜。 如果只存在一个这样的堆，那么先手只要一开始就拿这一堆，同样可以胜利。否则后手一定可以拿到一个特殊的堆，那么后手的操作次数至少不会少于先手，后手胜。

再考虑石头数可以$>= A + B$的情况。我们称把所有堆的石子数mod $(A + B)$后的局面为约化后的局面，然后证明一个局面和它约化后的局面胜负情况是一样的。

证明：

如果约化后的局面后手必胜，那么显然原来的局面后手也必胜。因为后手只要采取下面的策略就可以获胜：如果先手取了$>= A + B$的堆，后手也跟着取那一堆，否则后手采取和约化后的局面对应的策略。

如果约化后的局面后手必败，那么约化后的局面，$>= 2 * B$的堆只有0个或1个，先手只要一上来就先取这样的堆，然后之后如果后手取了$>= A + B$的堆，先手就跟着他取，否则采取和约化后的局面对应的策略，这样就可以胜利了。

3. A < B. 枚举先手第一步取哪个，转化为上一种情况。

 #include <bits/stdc++.h>
 using namespace std;

 #define MAXN 100010
 int v[MAXN];
 int x, y, z, tot;

 void add(int t, int a, int b)
 {
     if (t < b) --tot;

     if (t >= a) ++x;
     if (t >= b && t < a) ++y;
     if (t >=  * b) ++z;
 }

 void del(int t, int a, int b)
 {
     if (t < b) ++tot;

     if (t >= a) --x;
     if (t >= b && t < a) --y;
     if (t >=  * b) --z;
 }

 int main()
 {
     int n, a, b;
     scanf("%d %d %d", &n, &a, &b);
     for (int i = ; i <= n; ++i)
         scanf("%d", &v[i]);

     int flag = ;
     if (a == b)
     {
         int cnt = ;
         for (int i = ; i <= n; ++i)
             cnt += v[i] / a;
         puts(cnt & ? "Zenyk":"Marichka");
     }
     else if (a > b)
     {
         x = y = z = , tot = n;
         for (int i = ; i <= n; ++i)
         {
             int t = v[i] % (a + b);
             add(t, a, b);
         }
         flag |= (tot%==) || z >=  || y;
         puts(!flag? "Zenyk":"Marichka");
     }
     else
     {
         x = y = z = , tot = n;
         for (int i = ; i <= n; ++i)
         {
             int t = v[i] % (a + b);
             if (t < a) --tot;

             if (t >= b) ++x;
             if (t >= a && t < b) ++y;
             if (t >=  * a) ++z;
         }

         for (int i = ; i <= n; ++i)
         {
             if (v[i] < a) continue;
             del(v[i] % (a + b), b, a);
             add((v[i] - a) % (a + b), b, a);

             flag |= (tot%==) || z >=  || y;
             add(v[i] % (a + b), b, a);
             del((v[i] - a) % (a + b), b, a);
         }
         puts(flag? "Zenyk":"Marichka");
     }
     return ;
 }

---

2016 Petrozavodsk Winter- Saratov SU Contest  Problem B Game on Bipartite Graph（证明留坑）

http://codeforces.com/gym/100886

题意：

给出一个二分图，一开始棋子在左边，两人轮流玩，每次沿着边移动，移动后那条边删去，谁不能动谁就输了。 点数<=100.

题解：
考虑一个先手赢的局面，那么棋子的轨迹一定是左右左右。。。左右， 对于左边的点，如果它不是起点，那么轨迹中一定有偶数条边和它关联。如果是起点，一定有奇数条。

如果右边存在一个点集S，使得左边和S相关的点中，仅有起点度数为奇数，那么先手必胜，他只要每次只往S集合里的点走就好了。  这个条件是充要的，不过反过来还不清楚为什么是对的。。。  高斯消元求是否存在这样的点集就好了。

 #include <bits/stdc++.h>
 using namespace std;

 #define N 100
 int e[N][N], a[N][N];
 bool inset[N];

 void guass(int n, int m)
 {
     int line = , i, j, k, col[N];
     for (i = ; i <= m && line <= n; ++i)
     {
         k = line;
         for (j = line + ; j <= n; ++j)
             if (a[j][i]) k = j;
         if (!a[k][i]) continue;

         if (k != line)
         {
             for (j = i; j <= m + ; ++j)
                 swap(a[k][j], a[line][j]);
         }

         for (j = line + ; j <= n; ++j)
         {
             if (a[j][i])
             {
                 for (k = i; k <= m + ; ++k)
                     a[j][k] ^= a[line][k];
             }
         }
         col[line++] = i;
     }
     --line;
     for (i = line + ; i <= n; ++i)
     {
         if (a[i][m + ])
         {
             return;
         }
     }

     int ans[N] = {};
     for (i = line; i >= ; --i)
     {
         int s = a[i][m + ];
         for (j = col[i] + ; j <= m; ++j)
             s ^= a[i][j] & ans[j];
         ans[col[i]] = inset[col[i]] = s;
     }
 }

 int main()
 {
     int n, m, edges, v, x, y;
     scanf("%d %d %d %d", &n, &m, &edges, &v);
     while (edges--)
     {
         scanf("%d %d", &x, &y);
         e[x][y]++;
     }
     for (int j = ; j <= m; ++j)
     {
         for (int i = ; i <= n; ++i)
             a[i][j] = e[i][j] & ;
     }
     a[v][m + ] = ;
     guass(n, m);

     while (true)
     {
         int t = -;
         for (int j = ; j <= m; ++j)
             if (e[v][j] && (t == - || inset[j]))
                 t = j;
         if (t == -)
         {
             puts("Player 2 wins");
             fflush(stdout);
             break;
         }
         --e[v][t], v = t;
         printf("%d\n", t);
         fflush(stdout);

         t = -;
         for (int i = ; i <= n; ++i)
             if (e[i][v]) t = i;
         if (t == -)
         {
             puts("Player 1 wins");
             fflush(stdout);
             break;
         }

         int newv;
         scanf("%d", &newv);
         --e[newv][v], v = newv;
     }

     return ;
 }

---

XVIII Open Cup named after E.V. Pankratiev. GP of Romania Problem L Xormites（证明留坑）

http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=010391

题意：

给出一个自然数序列，两个人轮流，每次从两头拿一个数， 每个人的得分是拿的数异或起来，得分多的人赢。

题解：
如果一开始所有的数异或和如果为0，那么肯定平局。

否则异或和非零，考虑异或和最高位非0的位置。显然最终两个人的得分这一位一个是0，一个是1.

所以其它位可以丢掉，只考虑这一位。

如果N是偶数，将下标奇数位置染成白色，偶数位置染成黑色，先手可以取走所有白色，或者所有黑色，所以先手必胜。

如果N是奇数，那么先手必须要取一个1，否则根据N-1是偶数，剩下的根据上一条后手必胜。

依次check先手拿哪头的1.

先手拿走一个1后，剩下的数xor起来是0，之后后手不管拿什么，先手必须都要和他拿的一样，否则会使xor起来非0且剩下偶数个数，后手必胜。

接下来就是一个我还不知道怎么证明的结论(CF讨论里petr提到了这个结论但没有给出证明)：

先手能每次模仿后手的取法，当且仅当剩下的序列是“S aabbccdd.... T”这样的形式，其中S和T是互为转置的01串。也就是说两头一段相等，中间相邻的相等。

 #include <bits/stdc++.h>
 using namespace std;

 #define MAXN 100010
 typedef long long LL;

 bool check(int l, int r, int a[])
 {
     if (l > r) return true;
     int ones = ;
     for (int i = l; i <= r; ++i)
         ones += a[i] == ;
     if ((ones >> ) & ) return false;

     while (l < r && a[l] == a[r]) ++l, --r;
     for (int i = l; i <= r; i += )
         if (a[i] ^ a[i + ]) return false;
     return true; 

 }

 int solve()
 {
     int n, sum = ;
     static int a[MAXN];
     scanf("%d", &n);
     for (int i = ; i <= n; ++i)
         scanf("%d", &a[i]), sum ^= a[i];
     if (sum == ) return ;
     if (n %  == ) return ;
     if (n == ) return ;

     for (int i = ; ; --i)
     {
         if ((sum >> i) & )
         {
             for (int j = ; j <= n; ++j)
                 a[j] = (a[j] >> i) & ;
             break;
         }
     }

     if (a[] && check(, n, a)) return ;
     if (a[n] && check(, n - , a)) return ;
     return -;
 }

 int main()
 {
     //freopen("in.txt", "r", stdin);

     int T;
     scanf("%d", &T);
     while (T--)
     {
         int res = solve();
         if (res == ) puts("First");
         else if (res == ) puts("Draw");
         else puts("Second");
     }

     return ;
 }

---

XVIII Open Cup named after E.V. Pankratiev. Grand Prix of Korea Problem J Game of Sorting

http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=010410

题目大意：

一个序列，每次只能从两头拿。谁操作完最后剩下的序列单调非降或者单调非增谁就赢。 Q个询问，每次问子区间[L, R]的结果。

题解：

1.如果一开始就单调，先手必败。

2.如果单调区间长度为区间长度-1， 那么先手必胜。

3.如果单调区间长度为区间长度-2：

　　3.a 如果[L + 1, R - 1]单调，显然先手必败。

3.b 如果[L, R - 2]单调， 显然先手必须先取A[L], 接着后手必须取A[L + 1]. 二分找到最多能两个两个取取多少次。

3.c 如果[L + 2, R]单调, 和3.b对称。

4. 如果单调区间长度 更小。

win[L, R] = !win[L, R - 1] | !win[L + 1, R] .

观察下图：

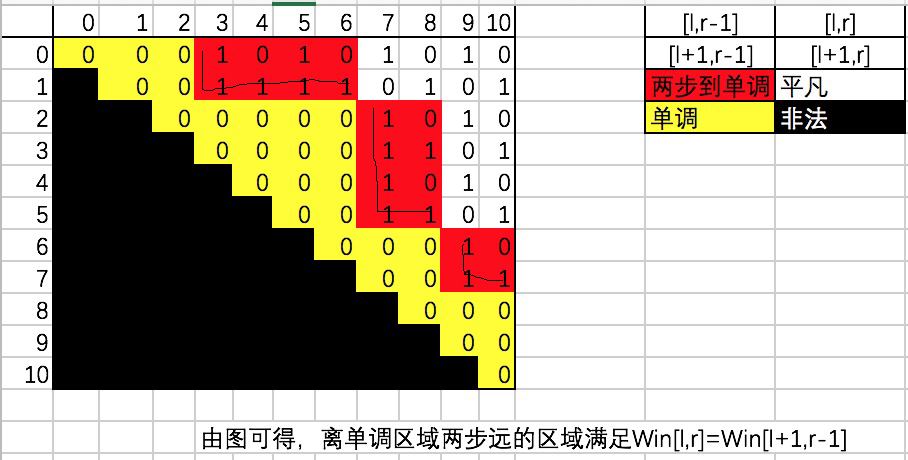
有win[L, R] = win[L + 1, R - 1]. 在上图中就是对角线元素相同， 单调区间长度为区间长度-2的情况实际上是为了求出一条对角线最左下角的那个。

根据这个，只要二分出可以确定的区间[L + k, R - k]再判断即可。

细节比较多的博弈题。

 #include <bits/stdc++.h>
 using namespace std;

 #define MAXN 1000010
 typedef long long LL;

 int a[MAXN], L[MAXN], f[MAXN], g[MAXN];

 int type(int l, int r)
 {
     if (l >= r) return ;
     if (L[r] <= l) return ;
     if (L[r] == l +  || L[r - ] <= l) return ;
     if (L[r - ] == l + ) return ;
     if (L[r - ] <= l) return ;
     if (L[r] <= l + ) return ;
     return ;
 }

 int solve(int l, int r)
 {
     int len = r - l + ;
     int kl, kr, kmid;
     kl = , kr = r - l + ;
     while (kl < kr)
     {
         kmid = (kl + kr) >> ;
         if (type(l + kmid, r - kmid) == ) kl = kmid + ;
         else kr = kmid;
     }
     l += kl;
     r -= kl;
     //cout << l << " " << r << " " << type(l + 1, r - 1) << endl;
     if (L[r] <= l) return ;
     if (L[r] == l +  || L[r - ] <= l) return ;
     if (L[r - ] == l + ) return ;
     else if (L[r - ] <= l)
     {
         kl = , kr = len / ;
         while (kl < kr)
         {
             kmid = (kl + kr) >> ;
             if (type(l + kmid * , r) == type(l, r)) kl = kmid + ;
             else kr = kmid;
         }
         l += kl * ;
         return solve(l, r);
     }
     else
     {
         kl = , kr = len / ;
         while (kl < kr)
         {
             kmid = (kl + kr) >> ;
             if (type(l, r - kmid * ) == type(l, r)) kl = kmid + ;
             else kr = kmid;
         }
         r -= kl * ;
         return solve(l, r);
     }
 }
 int main()
 {
     //freopen("in.txt", "r", stdin);

     int n, Q, l, r;
     scanf("%d", &n);
     for (int i = ; i <= n; ++i)
         scanf("%d", &a[i]);
     L[] = f[] = g[] = ;
     for (int i = ; i <= n; ++i)
     {
         if (a[i] >= a[i - ]) f[i] = f[i - ];
         else f[i] = i;
         if (a[i] <= a[i - ]) g[i] = g[i - ];
         else g[i] = i;
         L[i] = min(f[i], g[i]);
     }
     scanf("%d", &Q);
     while (Q--)
     {
         scanf("%d %d", &l, &r);
         int res = solve(l, r);
         if (res == ) puts("Alice");
         else puts("Bob");
     }
     return ;
 }

ps:

win[L, R] = win[L + 1, R - 1]的证明：

1. 如果win[L + 1, R - 1] = 0. 先手取L，后手取R，先手就输了；先手取R，后手取L，先手也是输。 所以win[L, R] = 0.

2. 如果win[L + 1, R - 1] = 1. 那么win[L + 2, R - 1] win[L + 1, R - 2]至少有一个等于1. 根据对称性假设win[L + 2, R - 1] = 1。 先手只要先取L, 然后如果后手取L + 1， 先手就取R， 如果后手取R， 先手就取L + 1.  所以先手可以胜利。 win[L, R] = 1.

---

Petrozavodsk Winter-2015. Jagiellonian U Contest Problem J. Game

http://opentrains.snarknews.info/~ejudge/team.cgi?contest_id=1456&locale_id=0

题目大意：一个序列，每次只能从两头拿。然后给出一些终止序列，即如果轮到某个人的时候，当前序列是终止序列，他就输了。 如果全被拿完，那么平局。问先手胜利还是后手胜利还是平局。（每个人如果他能获胜他就不会去平局）

题解：

1.首先有一个平局比较恶心。可以做两边，第一遍定义平局算先手胜利，第二遍定义平局算后手胜利。 如果第二遍先手胜利，那么先手肯定胜利。 否则先手肯定不能胜利，那么看他能不能平局。 只要看第一遍先手能不能胜利，能胜利就是平局，否则就是后手胜利。

2.定义win[L, R, draw = 0 or 1]表示只考虑[L, R]这一段，且平局算先手胜利（draw = 1）/ 失败(draw = 0) 的结果。 check(L, R)表示[L, R]这一段是否是终止序列。先考虑一些特殊的情况： 按顺序check下面每一条。

2.1 如果 check(L, R) = 1.     win[L, R, draw] = 0.

2.2 如果L = R， win[L, R, draw] = draw.

2.3 如果check(L, R - 1) = 1 or check(L + 1, R)  = 1。 那么显然先手可以获胜。

2.4 如果L + 1 = R, win[L, R, draw] = draw.

2.5 如果check(L + 2, R ) = 1. win[L, R, draw] = !win[L, R - 1, !draw]. 因为先手不能取L， 取L得话后手取L+1就凉了。 check(L, R - 2) = 1时同理有win[L, R, draw] = !win[L + 1, R, !draw].

2.6 如果check(L + 1, R - 1) = 1, win[L, R, draw] = 0.   因为先手随便取哪段，后手取另外一端就好了。

2.7 如果L + 2 = R, win[L, R, draw] = draw.

接下来是最重要的一条性质：win[L, R, draw] = win[L + 1, R - 1, draw].  证明同上一题的ps部分。

1. 如果win[L + 1, R - 1] = 0. 先手取L，后手取R，先手就输了；先手取R，后手取L，先手也是输。 所以win[L, R] = 0.

2. 如果win[L + 1, R - 1] = 1. 那么win[L + 2, R - 1] win[L + 1, R - 2]至少有一个等于1. 根据对称性假设win[L + 2, R - 1] = 1。 先手只要先取L, 然后如果后手取L + 1， 先手就取R， 如果后手取R， 先手就取L + 1.  所以先手可以胜利。 win[L, R] = 1.

最后考虑如何求check(L, R)。 其实只要暴力检验每一个长度为R - L + 1的终止序列就好了，因为相同区间长度只会被check常数次。

 #include <bits/stdc++.h>
 using namespace std;

 #define N 1000010

 vector<vector<int> > lis[N];
 int n, m;
 int a[N];

 bool check(int l, int r)
 {
     assert(l <= r);
     int len = r - l + ;
     for (auto s: lis[len])
     {
         int flag = ;
         for (int i = ; i < len && flag; ++i)
             if (s[i] ^ a[l + i]) flag = ;
         if (flag) return true;
     }
     return false;
 }

 int win(int l, int r, int draw)
 {
      assert(l <= r);

     if (check(l, r)) return ;
     if (l == r) return draw;

     if (check(l, r - ) || check(l + , r)) return ;
     if (l +  == r) return draw;

     if (check(l + , r - )) return ;
     if (check(l, r - )) return !win(l + , r, draw ^ );
     if (check(l + , r)) return !win(l, r - , draw ^ );
     if (l +  == r) return draw;

     return win(l + , r - , draw);

 }

 void solve()
 {
     scanf("%d", &n);
     for (int i = ; i < n; ++i)
         scanf("%d", &a[i]);
     scanf("%d", &m);

     while (m--)
     {
         int k, x;
         scanf("%d", &k);
         vector<int> s;
         for (int i = ; i < k; ++i)
             scanf("%d", &x), s.push_back(x);
         if (k < n) lis[k].push_back(s);

     }
     int win1 = win(, n - , );
     int win2 = win(, n - , );

     assert(!(win1 ==  && win2 == ));
     if (win1 & win2) puts("FIRST");
     else if (win1 | win2) puts("DRAW");
     else puts("SECOND"); 

     for (int i = ; i <= n; ++i) lis[i].clear();

 }

 int main()
 {
     int T;
     scanf("%d", &T);
     while (T--)
     {
         solve();
     }
     return ;
 }