K-means聚类算法与EM算法

K-means聚类算法

K-means聚类算法也是聚类算法中最简单的一种了，但是里面包含的思想却不一般。

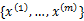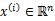聚类属于无监督学习。在聚类问题中，给我们的训练样本是，每个，没有了y。

K-means算法是将样本聚类成k个簇（cluster），具体算法描述如下：

1、 随机选取k个聚类质心点（cluster centroids）为。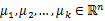

2、 重复下面过程直到收敛 {

对于每一个样例i，计算其应该属于的类

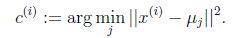
对于每一个类j，重新计算该类的质心

}

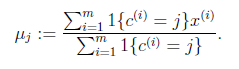
K是我们事先给定的聚类数，代表样例i与k个类中距离最近的那个类，的值是1到k中的一个。质心代表我们对属于同一个类的样本中心点的猜测，重复迭代第一步和第二步直到质心不变或者变化很小。

K-means面对的第一个问题是如何保证收敛，前面的算法中强调结束条件就是收敛，可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性，我们定义畸变函数（distortion function）如下：

J函数表示每个样本点到其质心的距离平方和。

K-means是要将J调整到最小。

假设当前J没有达到最小值，那么首先可以固定每个类的质心，调整每个样例的所属的类别来让J函数减少，同样，固定，调整每个类的质心也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时，和c也同时收敛。

由于畸变函数J是非凸函数，意味着我们不能保证取得的最小值是全局最小值，也就是说k-means对质心初始位置的选取比较感冒，但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优，那么可以选取不同的初始值跑多遍k-means，然后取其中最小的J对应的和c输出。

下面累述一下K-means与EM的关系：

首先回到初始问题，我们目的是将样本分成K个类，其实说白了就是求一个样本例的隐含类别y，然后利用隐含类别将x归类。由于我们事先不知道类别y，那么我们首先可以对每个样例假定一个y吧，但是怎么知道假定的对不对呢？怎样评价假定的好不好呢？

我们使用样本的极大似然估计来度量，这里就是x和y的联合分布P（x,y）了。如果找到的y能够使P(x,y)最大，那么我们找到的y就是样例x的最佳类别了，x顺手就聚类了。但是我们第一次指定的y不一定会让P(x,y)最大，而且P(x,y)还依赖于其他未知参数，当然在给定y的情况下，我们可以调整其他参数让P(x,y)最大。但是调整完参数后，我们发现有更好的y可以指定，那么我们重新指定y，然后再计算P(x,y)最大时的参数，反复迭代直至没有更好的y可以指定。

这个过程有几个难点：

第一怎么假定y？是每个样例硬指派一个y还是不同的y有不同的概率，概率如何度量。

第二如何估计P(x,y)，P(x,y)还可能依赖很多其他参数，如何调整里面的参数让P(x,y)最大。

EM算法的思想：E步就是估计隐含类别y的期望值，M步调整其他参数使得在给定类别y的情况下，极大似然估计P(x,y)能够达到极大值。然后在其他参数确定的情况下，重新估计y，周而复始，直至收敛。

从K-means里我们可以看出它其实就是EM的体现，E步是确定隐含类别变量，M步更新其他参数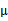来使J最小化。这里的隐含类别变量指定方法比较特殊，属于硬指定，从k个类别中硬选出一个给样例，而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程，有目标函数，也有参数变量，只是多了个隐含变量，确定其他参数估计隐含变量，再确定隐含变量估计其他参数，直至目标函数最优。

EM算法就是这样，假设我们想估计知道A和B两个参数，在开始状态下二者都是未知的，但如果知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

EM的意思是“Expectation Maximization”

http://blog.csdn.net/zouxy09/article/details/8537620