求最小生成树（暴力法，prim，prim的堆优化，kruskal）

求最小生成树（暴力法，prim，prim的堆优化，kruskal）

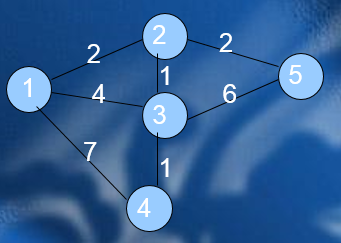
5 7
1 2 2
2 5 2
1 3 4
1 4 7
3 4 1
2 3 1
3 5 6

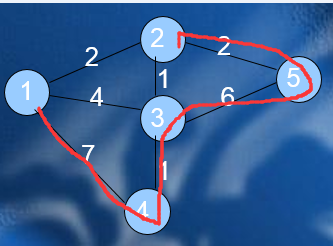
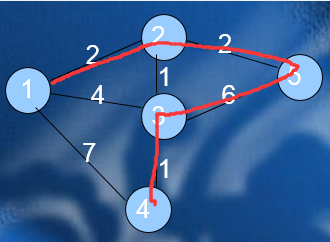
我们采用的是dfs的回溯暴力，所以对于如下图，只能搜索到3条路，就是那种dfs的路。

思路：

暴力求最小生成树
求这个图的最小生成树
我就要看有多少个点被选进去了，vis数组就好，并且用个n来表示已经被选的点的个数
然后记录所以已经选了的路径和

 #include <bits/stdc++.h>
 #define INFINITE 0x3fffffff
 using namespace std;
 struct node{
     int v;
     int w;
     node(int v,int w){
         this->v=v;
         this->w=w;
     }
 };
 vector<node> vec[];
 int edgeNum[];
 int n,m;
 bool vis[];

 int minDis=INFINITE; 

 void addEdge(int u,int v,int w){
     edgeNum[u]++;
     vec[u].push_back(node(v,w));
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         addEdge(u,v,w);
         addEdge(v,u,w);
     }
 }

 /*
 暴力求最小生成树
 求这个图的最小生成树
 我就要看有多少个点被选进去了，vis数组就好，并且用个n来表示已经被选的点的个数
 然后记录所以已经选了的路径和
 */
 //记录起点，记录选了个点
 void search(int start,int dis,int cur){
     //边界一定要清楚
     //而且这里是5不是6
     if(cur==){//这里写成n==n 第几错误傻逼错误满天飞
         cout<<dis<<endl;
         if(dis<minDis){
             minDis=dis;
         }
         return ;
     }
     for(int i=;i<edgeNum[start];i++){

         int v=vec[start][i].v;
         int w=vec[start][i].w;
         //cout<<vis[v]<<endl;
         if(!vis[v]){
             cout<<start<<" "<<v<<" "<<w<<endl;
             vis[v]=true;
             search(v,dis+w,cur+);
             vis[v]=false;
         }

     }
 } 

 int main(){
     freopen("in.txt","r",stdin);
     init();
     vis[]=true;//这句话居然在search下面
     search(,,); 

     cout<<minDis<<endl;
     return ;
 } 

上述代码再说几点

1、上述代码并不能解决最小生成树，只能求出DFS的最小生成树情况，所以还需要其它的暴力方法

2、回溯有问题

3、回溯的边界请想清楚

4、变量的初始值请想清楚，dis初始时0不是INFINITE

5、第71行我开始居然写到了72行之下

6、写代码太不专心了，傻逼错误太多了

7、第45行也是

8、暴力搜索的话应该是搜索已经求出来的集合到未求出来的集合的路径，这样可以暴力求出最小生成树

9、树形dp可以求出最小生产树，自然记忆化递归也可以

代码2，把回溯中的变量dis写在了外面，更好理解回溯

 #include <bits/stdc++.h>
 #define INFINITE 0x3fffffff
 using namespace std;
 struct node{
     int v;
     int w;
     node(int v,int w){
         this->v=v;
         this->w=w;
     }
 };
 vector<node> vec[];
 int edgeNum[];
 int n,m;
 bool vis[];
 int dis=;
 int minDis=INFINITE; 

 void addEdge(int u,int v,int w){
     edgeNum[u]++;
     vec[u].push_back(node(v,w));
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         addEdge(u,v,w);
         addEdge(v,u,w);
     }
 }

 /*
 暴力求最小生成树
 求这个图的最小生成树
 我就要看有多少个点被选进去了，vis数组就好，并且用个n来表示已经被选的点的个数
 然后记录所以已经选了的路径和
 */
 //记录起点，记录选了个点
 void search(int start,int cur){
     //边界一定要清楚
     //而且这里是5不是6
     if(cur==){//这里写成n==n 第几错误傻逼错误满天飞
         cout<<dis<<endl;
         if(dis<minDis){
             minDis=dis;
         }
         return ;
     }
     for(int i=;i<edgeNum[start];i++){

         int v=vec[start][i].v;
         int w=vec[start][i].w;
         //cout<<vis[v]<<endl;
         if(!vis[v]){
             cout<<start<<" "<<v<<" "<<w<<endl;
             vis[v]=true;
             dis+=w;
             search(v,cur+);
             dis-=w;
             vis[v]=false;
         }

     }
 } 

 int main(){
     freopen("in.txt","r",stdin);
     init();
     vis[]=true;//这句话居然在search下面
     search(,); 

     cout<<minDis<<endl;
     return ;
 } 

prim

 #include <bits/stdc++.h>
 #define INFINITE 0x3fffffff
 using namespace std;
 struct node{
     int v;
     int w;
     node(int v,int w){
         this->v=v;
         this->w=w;
     }
 };
 vector<node> vct[];
 int edgeNum[];
 int n,m;
 bool vis[];
 //集合a到集合b的最短距离
 int dis[];
 int ans[];
 int juli=; 

 void printDis(){
     for(int i=;i<=n;i++){
         cout<<dis[i]<<" ";
     }
     cout<<endl;
 }

 void addEdge(int u,int v,int w){
     edgeNum[u]++;
     vct[u].push_back(node(v,w));
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         addEdge(u,v,w);
         addEdge(v,u,w);
     }
 }

 void prim(int start){
     memset(dis,0x3f,sizeof(dis));
     vis[start]=true;
     dis[start]=;
     ans[]=start;
     //时间复杂度 e+n^2
     for(int i=;i<=n;i++){
         //更新
         for(int j=;j<edgeNum[start];j++){
             int v=vct[start][j].v;//这里的j写成i了
             int w=vct[start][j].w;//这里的j写成i了
             if(!vis[v]&&w<dis[v]){
                 dis[v]=w;
             }
         } 

         //找最小
         int minv=INFINITE,min_i;
         for(int j=;j<=n;j++){
             if(!vis[j]&&dis[j]<minv){//这里的vis写成了dis，这些sb错误真的要爆了我
                 minv=dis[j];
                 min_i=j;
             }
         }
         juli+=dis[min_i];
         vis[min_i]=true;
         ans[i]=min_i;
         start=min_i;
     }
 }

 void print(){
     cout<<juli<<endl;
     for(int i=;i<=n;i++){
         cout<<ans[i]<<" ";
     }
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     prim();
     print();
     return ;
 }

上面代码说几点：

1、总的思路：集合a到集合b的最短距离，并不是新选的点到其它点的距离

2、还是有超级多傻逼错误

3、52,53行： 这里的j写成i了

4、62行，vis写成dis，其它位置的dis写成vis

5、每一轮里面：更新+找最小

6、加强复习，这个最小生成树真的弄了一万遍了

7、在代码中看时间复杂度，时间复杂度 e+n^2

堆优化的prim

 #include <bits/stdc++.h>
 #define INFINITE 0x3fffffff
 using namespace std;
 struct node{
     int v;
     int w;
     node(int v,int w){
         this->v=v;
         this->w=w;
     }
 };
 vector<node> vct[];
 int edgeNum[];
 int n,m;
 bool vis[];
 //集合a到集合b的最短距离
 int dis[];
 int ans[];
 int juli=; 

 void printDis(){
     for(int i=;i<=n;i++){
         cout<<dis[i]<<" ";
     }
     cout<<endl;
 }

 void addEdge(int u,int v,int w){
     edgeNum[u]++;
     vct[u].push_back(node(v,w));
 }

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         addEdge(u,v,w);
         addEdge(v,u,w);
     }
 }

 struct myCmp{
     bool operator ()(int a,int b){//忘记写(),之前写了被用了
         return dis[a]>dis[b];
     }
 };
 priority_queue<int,vector<int>,myCmp> q;
 void prim1(int start){
     int cnt=;
     memset(dis,0x3f,sizeof(dis));
     q.push(start);//这里写成了push_back
     dis[start]=;
     while(!q.empty()){
         int u=q.top();
         q.pop();
         if(vis[u]) continue;
         vis[u]=true;
         ans[++cnt]=u;
         juli+=dis[u];
         for(int i=;i<edgeNum[u];i++){
             int v=vct[u][i].v;
             int w=vct[u][i].w;
             if(!vis[v]&&w<dis[v]){
                 dis[v]=w;
                 q.push(v);
             }
         }
     }

 }

 void print(){
     cout<<juli<<endl;
     for(int i=;i<=n;i++){
         cout<<ans[i]<<" ";
     }
     cout<<endl;
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     prim1();
     print();
     return ;
 }

关于上面代码说几点：

1、因为dijkstra算法可以看成prim算法的特例，因为都是集合到集合的距离，不过dijkstra中的一个集合只有起始元素

2、所以两者算法极其相识，堆优化也是几乎一样

3、傻逼错误还是很多

4、52行的push写成了push_back，因为queue是push，vector是pushback

5、重载（）的（）写了被用了，所以导致漏掉了

6、时间复杂度：e+nlogn

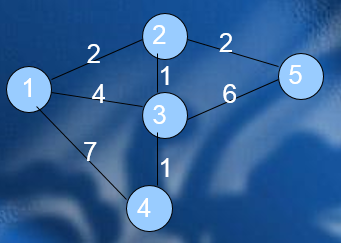
kruskal

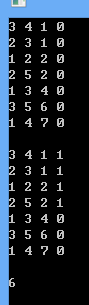
 #include <bits/stdc++.h>
 using namespace std;
 struct edgeNode{
     int u;
     int v;
     int w;
     bool vis;
     bool operator <(const edgeNode &p) const{
         return w<p.w;
     }
 }edge[];
 //father不是边的father，而是点的father
 int fa[];
 int n,m;
 int juli=;

 void print();

 void init(){
     cin>>n>>m;
     for(int i=;i<=m;i++){
         int u,v,w;
         cin>>u>>v>>w;
         edge[i].u=u;
         edge[i].v=v;
         edge[i].w=w;
     }
 }

 //int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
 int find(int x){
     if(x==fa[x]) return x;
     return fa[x]=find(fa[x]);
 } 

 void kruskal(){

     for(int i=;i<=n;i++) fa[i]=i;
     for(int i=;i<=m;i++){
         int x=find(edge[i].u);
         int y=find(edge[i].v);
         if(x!=y) {
             edge[i].vis=true;
             juli+=edge[i].w;
             //这样就已经实现了把集合相连 
             fa[y]=x;
         }
     }
 }

 int main(){
     freopen("in.txt","r",stdin);
     init();
     sort(edge+,edge++m);
     print();
     kruskal();
     print();
     cout<<juli<<endl;
     return ;
 }
 void print(){
     for(int i=;i<=m;i++){
         cout<<edge[i].u<<" "<<edge[i].v<<" "<<edge[i].w<<" "<<edge[i].vis<<endl;
     }
     cout<<endl;
 }

关于上面代码说几点：

1、father不是边的father，而是点的father

2、46行fa[y]=x;这样就已经实现了把集合相连

3、第31行并查集的两行代码要记下来，一个是叶子，非叶子怎么办

4、第8行结构体里面重载运算符

5、多复习