吴恩达机器学习103：SVM之大间隔分类器的数学原理

1.向量内积：

　　(1)假设有u和v这两个二维向量：，接下来看一下u的转置乘以v的结果，u的转置乘以v也叫做向量u和向量v的内积，u是一个二维向量，可以将其在图上画出来，如下图所示向量u：

　　

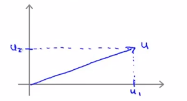
　　在横轴上它的值就是某个u_1，在纵轴上它的高度就是某个值u_2,即U的第二个分量，那么现在就容易得出向量u的范数，||u||就表示u的范数或者u的欧几里得长度，即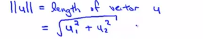

　　同理对于向量v而言，向量v有两个分量v1和v2，横轴是v1，纵轴是v2，因此向量v就会是下面这样的

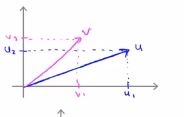
　　接下来看看如何计算u和v的内积的，具体做法如下，将向量v投影到u上，因此需要做一个直角投影或者一个90度角的投影，如下将其投影到u上，接下来的就是要测一下p的长度，我们标记这条红线的长度 为p，因此p就是向量v在向量u上的投影长度或者说量，因此可以用u的内积乘以v，它的结果等于p乘上u的范数或者长度，即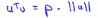，最后可以得出：

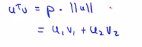，这个公式会得出最终的答案，如果你进行相反的计算，只是把u和v交换一下即可。从上面的讨论可以知道，u的范数是一个实数，，同时p也是一个实数，因此u的准直乘以v就是两个实数，也就是p的长度乘以u的范数，最后需要注意一点就是，如果你着眼于范数p，p实际上是有值的，即它可能是正值，也可能是负值。

　　(2)示例。如果u和v分别是如下的两个向量，如果u和v之间的夹角大于90度的话，我们将v投影到u上，

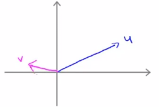
我们会得到下面这样的一个投影，红色的部分就是p的长度，这个时候u的转置乘以v就等于p乘以u的范数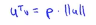，唯一不同的是这里的p值是负数，因此在内积的计算中，如果u和v之间存在夹角，如果夹角小于90度的话，那么这条红线的长度就是正值，相反如果这个夹角大于90度的话，那么这里的p值就是负数，两个向量的内积就是负数，

　　

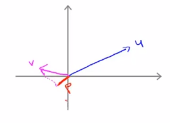
　　(3)SVM决策边界：我们首先忽略θ0，将其设置为0，为了更容易的画图，我们将特征数n设置为2，这样我们就只有两个特征向量x1,x2，现在我们看看这个支持向量机的优化目标函数，当n=2的时候，即我们只有两个特征向量时，这个式子可以写成，因为我们只有两个参数θ1和θ2，所以接下来可以将其写成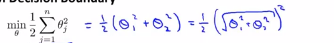：，括号中的这项就可以写成：

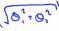=||θ||，意思是我们将向量θ写成这样的形式：θ1  θ2，那么刚刚划线的这项就是θ的长度或者范数，如同这里的当θ0等于0的时候，那么这里的向量就是θ1和θ2向量的长度。因此这意味着我们的目标函数等于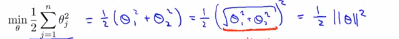：，所以对于优化目标函数来说，支持向量机做的是最小化参数θ的范数的平方。

　　(4)接下来我们需要考虑一下这些项θ的转置乘以x，然后深入理解一下他们的作用，给定一个参数θ以及给定一个样本x会等于什么呢？如下图所示，我们将θ和x都从向量的角度来进行考虑，

　　　　

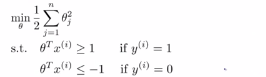
　　　　记住下图中的等式

　　

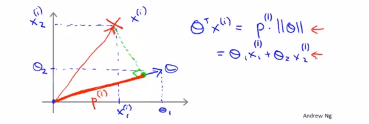
　　　　即在上述条件下，即θ的转置乘以x(i)，有大于等于1的，也有小于等于-1的

　　(5)当我们写入我们的优化目标函数后，没有了θ的转置乘以x(i)，取而代之的是p(i)乘以θ的范数，所以可以写成下面的形式：

　　

　　我们考虑一下上面的这个样本，然后继续使用之前的简化方法进行简化， 即θ0=0，让我们看看支持向量机会选择怎们样的边界，第一种选择方式：假设支持向量机选择这个决策边界，这并不是一个很好的选择，因为它的间距很小，离训练样本的距离很近，让我们看看为什么支持向量机为什么不选择它，对于这种参数，我们可以看到，参数向量θ事实上是与决策边界90度正交的。令θ0=0意味着决策边界必须通过原点(0,0)，现在我们看一下这对于优化目标函数意味着什么？比如说这个样本，假设第一个样本x(1)，

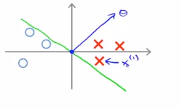
　　如果要考察样本到参数θ的投影，那么下图所示的短的红线就是p(1)，他是非常短的

　　

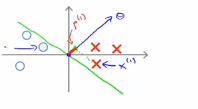
　　同样的对于下图的样本中，有一个样本为x(2)，下图中的洋红色就是p(2)，即样本在向量θ上的投影，p(2)实际上是一个负值，因为其实朝着相反的方向，这个向量与参数θ的夹角大于90度，因此p(2)的值就会小于0，我们发现，对于p(i)是非常小的数

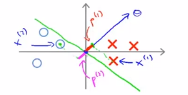
　　我们考虑优化目标函数，就会发现，对于正样本而言，我们需要p(i)乘以θ的范数能够大于等于1，即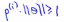，但是如果这里的p(1)特别的小，这就意味着我们需要θ的范数特别大，即||θ||要比较大

　　相似的，对于负样本而言，我们需要p(2)乘以θ的范数小于或者等于-1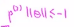，，这里p(2)是一个非常小的数，唯一的办法就是让θ的范数特别大，但是优化目标函数需要做的是，找到一套参数θ，来使得其范数足够的小，因此这个对于选择参数向量而言不是一个好方向

　　在这里，决策树可以选择这样的一个决策树边界，现在的图像上会有很大的不同

　　如果这是，那么对应的参数θ的方向就是下面蓝色箭头的方向，决策边界是绿色边界，可以得到样本点的边界长度是p(1)

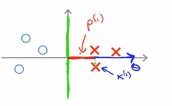
　　类似的可以做如下方式的投影，得到p(2)，其中p(2)的值是小于0的，可以看到，p(1)和p(2)的长度明显比上面的计算长度要长，现在p(1)变大了，因此θ的范数就可以变小了

　　

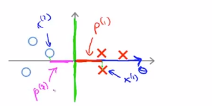
　　上面就意味着，通过选择下面的决策边界，而不是上面的那个决策边界，SVM可以使得参数θ的范数变小很多，也就是使得θ的范数的平方变小，这就是为什么svm会选择下面的假设函数，这就是svm是如何产生大间距分类现象的。

　　总结一下：

　　　　(1)下面这条绿色直线即绿色的决策边界，我们希望正负样本投影到θ的值足够的大，要做到这一点的唯一方式就是，让决策边界周围的点到决策边界保持大间距，这就是正样本和负样本之间的间隔，实际上间隔的值就是p1,p2,p3等值，通过让间距变大，svm最终可以输出一个比较小的θ范数，这就是支持向量机优化目标函数所做的，这就是为什么支持向量机最终会找到最大间距分类器的原因

　　　　(2)自始至终使得参数θ0=0的原因是使得决策边界始终过原点