洛谷P1199 三国游戏——题解

题目传送

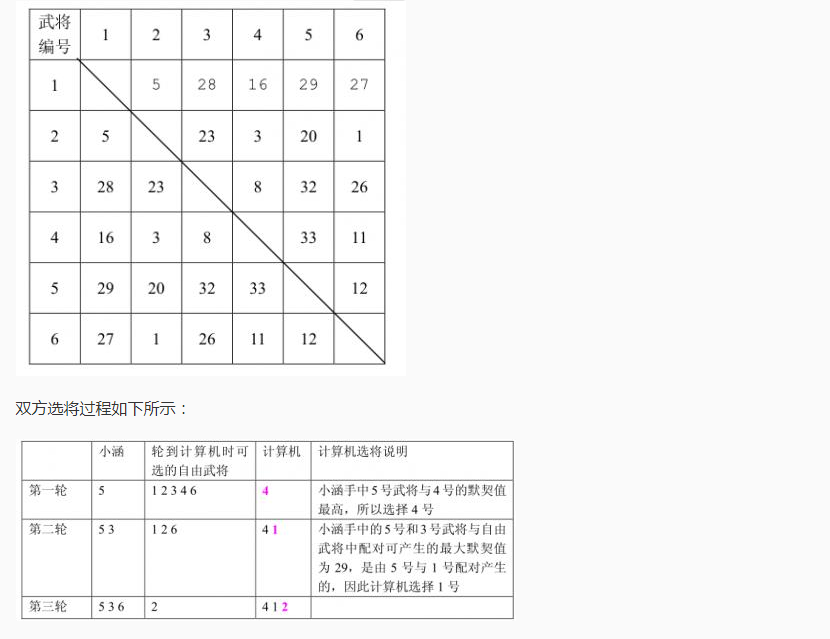
显然，在这样的数据范围下搜索是没希望的了。好好分析一下，发现小涵时不可能拿到与一个武将最默契的另一个武将了。所以考虑一下默契值次大的一对武将。

显然，对每一个武将来说，小涵是可以拿到默契值次大的武将。如果小涵拿到所有默契值次大的武将组合中最大的那个组合M会怎样？

考虑当小涵拿到所有默契值次大的武将组合后计算机的行动：计算机一定会去拿能跟小涵最后拿的武将组成目前最默契组合的自由武将。这个自由武将一定会与计算机第一次拿到的那个武将组成一个组合，这是人无法阻止的。考虑一下这个组合的默契值大小：如果这个组合N比小涵拿到 所有默契值次大的武将组合中最大的那个组合还要大，那么这个组合一定是某个武将能组成的最大组合。如果这个组合N比小涵拿到的第一个武将能组成的最默契的组合K还要大，显然所有默契值次大的武将组合中最大的那个组合就不是M了，与已知条件矛盾，故不成立；如果这个组合N比小涵拿到的第一个武将能组成的最默契的组合K还要大,显然N是比M更大的次大组合，与已知条件矛盾，故不成立。所以当小涵拿到所有默契值次大的武将组合中最大的那个组合M后，计算机下一步是拿不到比M更大的组合的。之后只要保证计算机拿不到最大的组合，小涵就一定会胜利。这样的话只要人按照计算机的策略拿将就行了。

见AC代码：

 #include<iostream>
 #include<cstdio>
 #include<algorithm>

 using namespace std;

 int a[][];

 inline bool cmp(int a,int b)
 {
     return a>b;
 }

 int main()
 {
     int n;
     cin>>n;
     for(int i=;i<n;i++)
         for(int j=i+;j<=n;j++)
         {
             cin>>a[i][j];
             a[j][i]=a[i][j];
         }
     for(int i=;i<=n;i++)
         sort(a[i]+,a[i]++n,cmp);
     int ans=;
     for(int i=;i<=n;i++) if(a[i][]>ans) ans=a[i][];
     cout<<"1\n"<<ans;
     return ;
 }